Java运算的精度和溢出问题

double和float的0.1问题

代码如下

public class demo2 {
    public static void main(String[] args) {
        float f=0.1f;
        double d=0.1;
        System.out.println(f==d);
        System.out.println(f);
        System.out.println(d);
    }
}

按理说,输出应该是：

true
0.1
0.1

实质上，编译后的结果却是

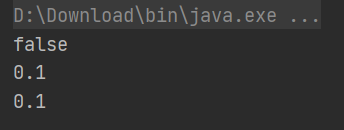
老师在抛出这个怪异现象后，作为之前有过编程基础的我老脸一红
在现场，就挺懵逼的

查了百度，float的0.1二进制形式是001111011 10011001100110011001101,根据符号位换算为10进制表达
的值精确应该是这样计算 110011001100110011001101乘以2的负27次方
实际值是0.100000001490116119384765625，这样就产生了实际误差，对于精度更大的double而言也是如此；
所以两者的比较值是false
这一查立马想起了之前C语言课上老师讲过的float值的0问题

public class demo2 {
    public static void main(String[] args) {
        double d=10/9;
        double a=1/10000000;
        System.out.println(d==1);
        System.out.println(a==0);
    }
}

编译出来的结果竟是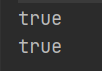
亦或者是“大数吃小数”

        float a=123456789101112f;
        float b=a+1; ;
        System.out.println(a==b);
        System.out.println(a);
        System.out.println(b);

编译输出：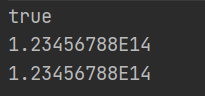
所以在java运算中，带有浮点数比较的运算尽量用功能类Bigdecimal

数值溢出问题

        int a=128;
        byte b=(byte)a;
        System.out.println(a);
        System.out.println(b);

编译输出：

128
-128
原因是将a强制转换成byte型时出现了溢出现象，这点是容易看出的
而转化为-128的原因是因为在计算机中数值都以补码储存
128在a中存储形式为0000 0000 0000 0000 0000 0000 1000 0000
在强制转换中，（byte）a保留了a的低8位并赋值给了b
此时b=1000 0000
按补码转换规则，1000 0000=-128
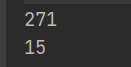
可以以此类推,将a的值修改为271=1 0000 1111
则验证输出的b为15

int a=271;
        byte b=(byte)a;
        System.out.println(a);
        System.out.println(b);