OO第三单元总结
终于走到了第三单元了,这个单元主要是对JML规格的考察。从个人角度来讲,很诚实的说,第三个单元会考察增删改查有点在我意料之外,一开始我个人觉得这种类型的设计并不会有太多复杂的地方需要考虑,也不会出什么bug,但是实际操作起来其实充满了很多让人意想不到的bug和错误(否则第二次作业之后我也不会必须重构我的代码了)。
那么首先我们先讲讲第三单元的核心内容,北京地铁线路图JML
一.JML语言梳理和应用工具链
语言梳理
在理论课上荣文戈老师给我们大致介绍了JML的意义所在,那就是用来表述一个方法要达到的目的或者是实现的功能是什么,一个合格的规格必须要做到覆盖所有可能的情况(包括一般情况和边界条件或是特殊情况),哪些变量会在这个方法中被改变,哪些不会。简单来说,规格就是告诉程序猿们,这个方法会传入几个参数,这几个参数进入这个方法时候是什么样子的,出来的时候需要是什么样子的,而程序猿只要按照规格去码代码,使代码和规格要求相符即可。所以规格就是设计者和程序写者之间心照不宣的默契,当然这也是程序出现问题时区别究竟是谁的锅的一种极好的办法。
JML规格的特点就是它并不关心一个方法实现的细节,例如我们到底是用了ArrayList还是HashMap,它只是简单的描述了我们对这个方法的预期(这非常面向对象)。一个规格包括三个部分:
-
前置条件,由requires字句来定义
-
副作用范围限定,由assignable列出这个方法能够修改的类成员属性
-
后置条件,由ensures字句来定义
就是这看似简单的三个部分,一个方法的前提和目的就已经被约束的明明白白了,不会有歧义,也不会有未考虑的情况,这就是JML所期望的契约精神。
应用工具链
-
OpenJML可以用来对已经实现的代码进行JML语法上的静态检查
-
JMLUnitNG可以根据JML自动生成TestNG测试
-
SMT Solver工具可以以静态方式来检查代码实现对规格的满足情况
二.OpenJML部署使用测试
这里我们利用伦佬提供的说明文档来部署测试一下OpenJML工具。
测试样例如下:
1 public class TestJML { 2 /*@ public normal_behaviour 3 @ ensures \result == (lhs - rhs) <==> (lhs > rhs); 4 @ ensures \result == 0 <==> !(lhs > rhs) || (lhs > 10000 || lhs < 0 || rhs > 10000 || rhs < 0); 5 */ 6 public static int substract(int lhs, int rhs) { 7 if (lhs > 10000 || lhs < 0 || rhs > 10000 || rhs < 0) { 8 return 0; 9 } else if (lhs > rhs) { 10 return lhs - rhs; 11 } else { 12 return 0; 13 } 14 } 15 16 public static void main(String[] args) { 17 int result = substract(114514,1919810); 18 result = substract(114,191); 19 result = substract(1145,19); 20 } 21 }
然后我们使用以下语句对这个java文件进行检查:
java -jar openjml.jar ~/desktop/openjml/TestJML.java
这句话执行完毕后并没有任何输出,为了确认是否通过OpenJML的检查,我在规格中进行了一点小的修改,把某个lhs改为了lsh,然后再次运行OpenJML,得到的结果如下:

于是我确认自己成功地通过了OpenJML的测试,后续还测试了一个小的方法,结果和这个类似,就不再赘述。
三.JMLUnitNG部署使用测试
在JMLUnitNG安装完成之后,我首先测试了讨论区的样例:
1 public class Demo { 2 /*@ public normal_behaviour 3 @ ensures \result == lhs - rhs; 4 */ 5 public static int compare(int lhs, int rhs) { 6 return lhs - rhs; 7 } 8 9 public static void main(String[] args) { 10 compare(114514,1919810); 11 } 12 }
~/Desktop java -jar jmlunitng-1_4.jar demo/Demo.java ~/Desktop javac -cp jmlunitng-1_4.jar demo/**/*.java ~/Desktop java -jar openjml.jar -rac demo/Demo.java
得到了这样的结果:
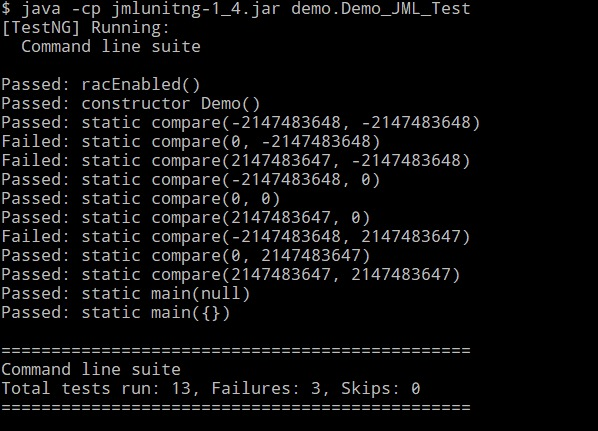
结果和预期的确是相符的,于是我接着对上面提到的的TestJML.java文件进行测试,但是运时发现会报出一些奇怪的错误:
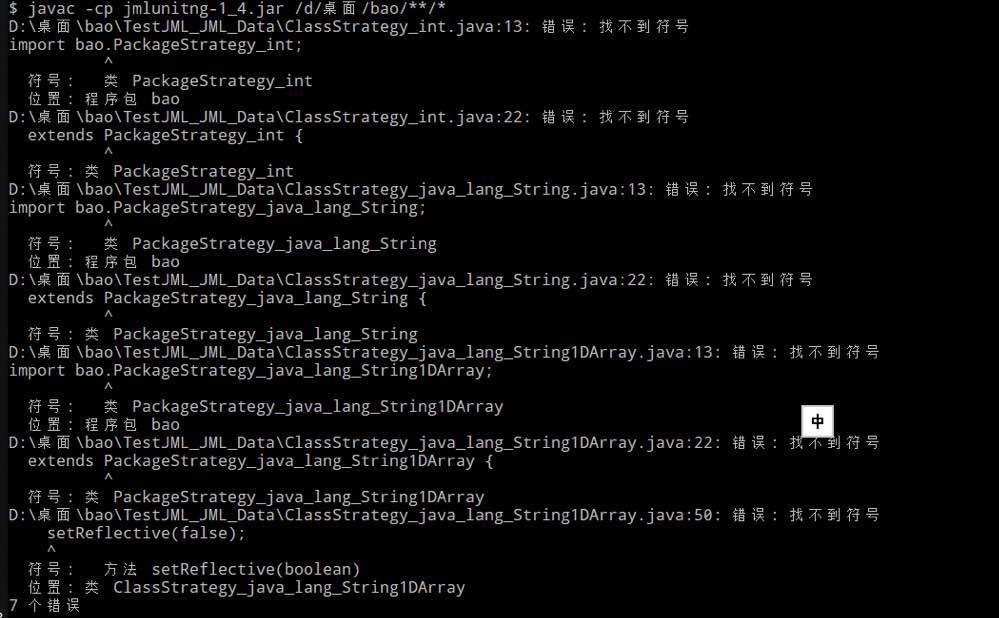
我对着这一堆乱七八糟的报错思考了很久也并没有发现问题的根源(事实证明JML工具有时候并没有我们想象中的那么好用),但是由于前面已经确认JMLUnitNG可以正常使用了,那么我就先继续后面的内容,如果后续问题得到了解决我会及时更新这篇博客。
四.三次作业大致思路
第一次作业
第一次作业只是简单的考察了路径的添加删除,然后还有几条简单的查询指令,比如路径的id,某一时刻容器内一共有多少个不同的节点。显然这并不是太难,但是其实一开始我做了一些非常愚蠢的操作,那就是无脑按照jml规格说明,申请了多个静态数组来存放路径和节点的信息,这样做在我程序的进一步完成中出现了很大的缺陷,例如查询某个路径的ID时,需要先对所有的path进行遍历,然后path中每一个node都进行比对,这样的做法使我程序的复杂度高达O(n^2),并且有些地方甚至无法把代码写下去,在进行了一番大的修整之后,我的第一次作业最终使用了HashMap来存放我的数据,这一做法在我的后两次作业里也得到了使用,并且我还对它们做了进一步的延伸。
在第一次作业里面关于迭代器的概念值得一提,我在第一次作业的时候花了一些时间去理解它的含义,大致的意思就是,java提供给了我们很多种容器来储存信息,这些容器的储存方式又各不相同,这样我们在对这些容器内部的信息进行遍历的时候,可能就遇到了需要使用不同的方法的问题,但是我们又知道,java设计的原则就是不能相信任何人,我们永远不知道谁会去使用这段程序,又到底是怎样使用,所以到底怎么做才能又让别人有办法遍历对象容器中的内容,又不暴露容器的内部细节呢?这就是迭代器的设计目的以及它所做的事,听起来好像很复杂,但是实际上在这三次作业里,我们只需要简单的返回一个nodes.iterator()就完事了。
第二次作业
第二次作业在第一次作业的基础上增加了两个新的读操作,分别是任意两个节点是否联通以及求两个节点之间的最短路,这样让我在一瞬间就想到了数据结构的北京地铁线路图(当然,在OO第三单元总结的课上,荣老师向我们阐明了看到问题应该先读懂设计者到底想让我们干什么,而不是直接望文生义联想到算法)。在这次作业里,最终我使用了DFS递归(最后在bug修复中发现这个方法存在致命的问题)来求两个节点是否联通,用Dijkstra算法来求两个节点之间的最短路。其实写代码的过程中并没有遇到什么很困难的地方,就是简单的加入了一个联通矩阵和一个最短路矩阵,很容易联想到我们在离散数学二里面学到的可达矩阵和距离矩阵,这个思路在当时的我看来是完全没有任何问题的,但是最后显然我在bug修复的时候吃了很大的亏。
第三次作业
相对而言第三次作业就比前两次作业要复杂不少了,添加了换乘的概念(当然我相信这也是大多数人意料之中的事情),计算两个节点之间最短的换乘数,最少的价格,计算联通块的数目,这些都在大多数人的准备之中,但是对于不满意度,这个概念的引入和计算方法着实让我有点摸不着头脑,但是实际上不知道它到底是什么也并不影响代码的实现。首先设计的基础框架是我大致重构过的第二次作业,计算三种最短路我采用了Floyd算法,具体为什么我在后面会说明,而对于联通块我采用了并查集的算法,最终事实证明这样的选择还是比较成功的。
五.一些算法和设计上的细节
个人觉得这个单元的作业涉及到的算法方面的问题比之前的两个单元都要复杂一些,所以单开一个板块来对我自己的作业中的一些点进行说明,希望可以对一些同学有所启发(如果有遗漏或者错误的地方也欢迎指正)。
第一次作业
首先是HashCode方法,我自己第一次作业在这里就发生了错误,首先在MyPath类中HashCode方法是必须进行重写的,因为按照要求我们已经重写了equals方法,不重写的后果是什么呢,那就是一旦在MyPathContainer类中我们使用了HashMap,那么使用get存放两个path型的key时,哪怕它们的内容一样,HashMap也不会认为二者是同一个key,因为默认情况下,HashCode方法是将对象的存储地址进行映射。我在第一次作业中是这样重写的hashCode方法:
public String hashCode(Path path) { String hash = new String(); for (int i = 0; i < path.size(); i++) { hash = hash + path.getNode(i); } return hash; }
显然是这样的方法是有问题的,当碰到类似path1:1 2 3和path2:1 23时,就会发生碰撞,像这样自己写的HashCode方法在互测的过程中我也碰到了不少没有处理好碰撞的例子,因此我还是建议直接使用jdk附带的HashCode,不论是正确性还是运行的速度大概率都比我们自己写的HashCode要好一些(当然最好的地方还是这么做不需要我们自己去动脑子想到底会不会发生碰撞)。在这里附上java有关HashCode部分的代码,相信聪明的同学们一定能理解:
@Override public int hashCode() { return Objects.hash(nodes, distinctNodes); }
public static int hash(Object... values) { return Arrays.hashCode(values); }
public static int hashCode(Object a[]) { if (a == null) return 0; int result = 1; for (Object element : a) result = 31 * result + (element == null ? 0 : element.hashCode()); return result; }
第二次作业
而在第二次作业里面有一个我个人认为非常关键的细节,不知道有多少同学和我一样,在自己的代码里分开计算了最短路和联通路两个容器里面的值,然后每次遇到有add或remove指令就对这两个graph进行一次更新,但是事实是,我们并不需要计算联通路,甚至根本不需要创建联通路这样一个容器,那么怎么判断两个点是否联通呢?首先我构造了一个这样的容器来储存最短路信息。
private HashMap<Integer, HashMap<Integer, Integer>> nodeList;//邻接矩阵 private HashMap<Integer, HashMap<Integer, Integer>> shortList;//最短路矩阵
shortList就是所谓的最短路矩阵,首先对它进行初始化,将邻接的连个点的最短距离赋值为1,否则赋值为10000,10000也就是我们设定的MAXLENGTH,然后再利用Floyd计算最短路。这样处理有什么好处呢,就是我们上面提到的,怎么判断两点是否联通,只需要看这两点的距离是否小于10000,就可以知道它们是否连通了,这样看起来我们似乎成功的减少了第二次作业将近一半的计算量,这里贴上代码。
//判断节点是否连通 public boolean isConnected(int fromNodeId, int toNodeId) throws NodeIdNotFoundException { if (nodeList.containsKey(fromNodeId)&& nodeList.containsKey(toNodeId)) { return (shortList.get(fromNodeId).get(toNodeId) < 10000); } else { throw new NodeIdNotFoundException(0); } }
第三次作业
下面就进入了最困难让不少人测评暴毙的第三次作业了,个人感觉我的处理方法相对比较暴力,既然最短路径可以使用Floyd,那么最少的换乘,最便宜的路线,不满意度最少的路径,也都可以用Floyd来实现,但是在实现的过程中我遇到了如何计算换乘的问题,非常感谢讨论区的大佬们给我提供了非常好的思路。
其实我们发现新增的三个读操作都是在求某种意义上的最短路径,唯一不同的地方就是增加了对线路转换的记录,每切换一次Path,就要记录一次换乘,但是有没有办法可以绕过pathid的判断呢,那就是按照图中的方法,只要我们做好每条边权值的初始化,就可以巧妙的避开目前访问的节点到底在哪条路径上的问题。针对初始化,这里还有一个问题要进行说明,那就是我们发现,求价格和不满意度时,首先要对每个路径的非邻接边进行一下初始化,这里我同样采用的是Floyd算法,这里附上具体的实现代码,仅供同学们参考:
//针对每一条路径内部做初始化 public void pathFloyd(Path path, HashMap<Integer,HashMap<Integer, Integer>> list, int num) { HashMap<Integer, HashMap<Integer, Integer>> ini = new HashMap<>(); //显然一条路径内部所有的点都是联通的 //那么为了避免重复的判断是否存在一个节点key //我们直接这条路径内部所有的节点put进HashMap for (int i = 0; i < path.size(); i++) { ini.put(path.getNode(i), new HashMap<>()); } //给相邻节点的边赋相应的权值 for (int i = 0; i < path.size() - 1; i++) { int before = path.getNode(i); int after = path.getNode(i + 1); int weight = 0; if (num == 1) {//针对不满意的初始化 weight = Integer.max( (before % 5 + 5) % 5, (after % 5 + 5) % 5); weight = (int)Math.pow(4, weight); } else if (num == 2) {//针对最少价格的初始化 weight = 1; } ini.get(before).put(after, weight); ini.get(after).put(before, weight); } //不相邻的点的边权值为10000 for (int i = 0; i < path.size(); i++) { int before = path.getNode(i); for (int j = 0; j < path.size(); j++) { int after = path.getNode(j); if (ini.get(before).containsKey(after)) { continue; } ini.get(before).put(after, 10000); } } //在内部利用了Floyd算法 for (Integer mid : ini.keySet()) { for (Integer from : ini.keySet()) { if (from.equals(mid)) { continue; } int fromToMid = ini.get(from).get(mid); if (fromToMid == 10000) { continue; } for (Integer to : ini.keySet()) { int midToTo = ini.get(mid).get(to); if (midToTo == 10000) { continue; } int fromToTo = ini.get(from).get(to); ini.get(from).put(to, Integer.min(fromToTo, fromToMid + midToTo)); if (ini.get(from).get(to) < list.get(from).get(to)) { list.get(from).put(to, ini.get(from).get(to)); } } } } }
在做好初始化的基础上,我们对graph再进行一次Floyd,就可以得到正确的结果了,这大概就是我个人这次作业整体的一些思路。
六.代码度量分析
第一次作业
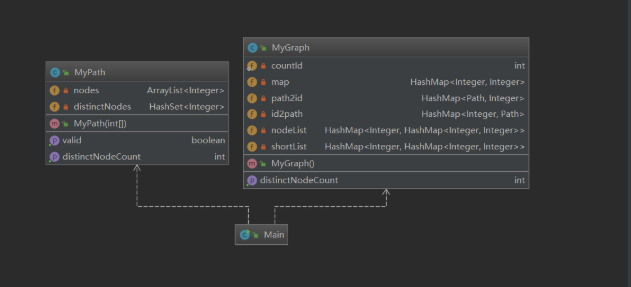
第一次作业结构比较简单,在这里不作赘述。
类图
复杂度度量表
| ev(G) | iv(G) | v(G) | OCavg | WMC | |
|---|---|---|---|---|---|
| Total | 132 | 152 | 180 | 150 | |
| Average | 1.26 | 1.45 | 1.71 | 1.43 | 5.17 |
第二次作业
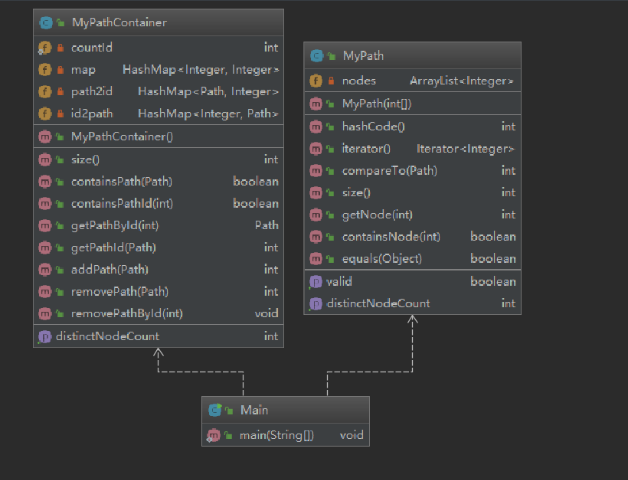
第二次作业在第一次作业的基础上添加了最短路和连通性的计算,所以复杂度相比于第一次要稍微高一些。
类图
复杂度度量表
| ev(G) | iv(G) | v(G) | OCavg | WMC | |
|---|---|---|---|---|---|
| Total | 167 | 221 | 268 | 219 | |
| Average | 1.25 | 1.65 | 2.00 | 1.63 | 6.26 |
第三次作业
第三次作业增加了三个类似最短路的计算,重点在于处理换乘,这里我们转化成了Path内部的最短路初始化。理论上来说,第三次作业只要优化的够好,复杂度和第二次应该相近,我们利用相应的计算工具分析得出的结果也的确是这样。
类图
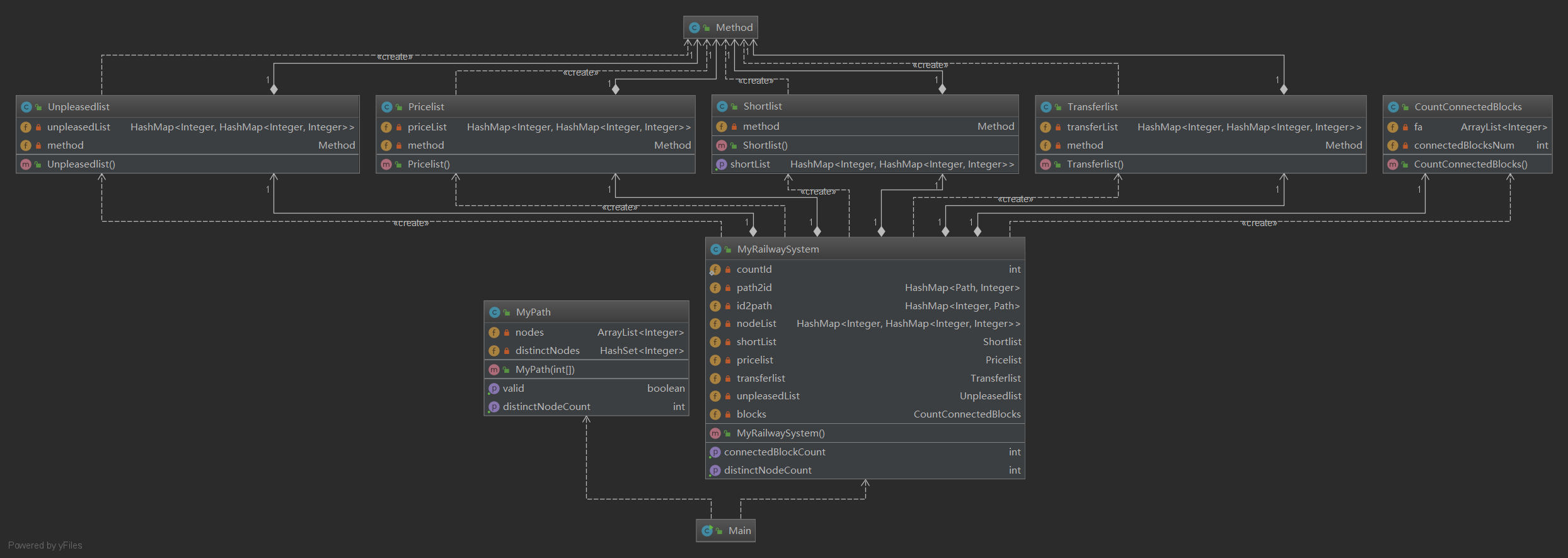
复杂度度量表
| ev(G) | iv(G) | v(G) | OCavg | WMC | |
|---|---|---|---|---|---|
| Total | 227 | 285 | 345 | 293 | |
| Average | 1.38 | 1.74 | 2.10 | 1.79 | 7.51 |
七.互测和bug修复
互测环节
这次的互测环节相信很多人的心情可以用下面这张图来代替。

好像很多狼人在各自的测评屋刀出了7/7,6/6一类的战绩,但是以我的个人经验来看,我觉得一旦有一个好的本地测评机,和一个代码较为靠谱的小伙伴,就大概率不会在强测互测出现这种情况。自己给自己做测评的思路很简单,随机生成5000条命令的代码我相信对于大多数人来说并不难写,但是怎么样才能更高效的检测自己的程序,我觉得分为两个部分,首先是程序的正确性,针对第三次,很多人其实主要错在了一条路径中出现闭环的情况,那么我们在测评的时候有意识的将点的重复度提高,例如所有的随机点都只在1-20甚至1-10中产生,这样出现各种闭环的概率就被大大提高了,我们也更容易发现这方面的问题。然后是程序的运行效率,那就要将点尽可能的分散开,在自己做测试的时候,我们甚至可以将点的范围提升到1-300,然后观察自己的运行时间,再进行相应的修改和优化(前提是正确性已经得到了保证)。对我个人而言,这样测评可能更加具有策略性,更容易发现自己的问题所在,一个5000行的错误样例往往让人很头疼,但是一个10行的样例就很容易找出问题,这也是我们自己写测评机需要追求的目标。
bug修复环节
又到了让好多人最头疼的bug修复环节了,不得不说,第二次的修复着实让我伤透了脑筋(最后一气之下直接重构然后选择了非合并修复),下面是我这次作业中出现的问题。
首先是第一次作业,整个程序并没有出现大的问题,但是依然存在一些小的毛病,首先是我在MyPath类中重写了HashCode方法,但是很不幸,我错误地遗漏了类似于Path1 = 1 2 3, Path2 = 1 23这样的数据,于是发生了碰撞,导致在互测中被应该是认真读了我代码的同学成功hack一次。第二个问题出在迭代器,当时还没有弄清除使用方法的我自以为是的写了一堆乱七八糟现在自己也不知道是什么的东西,导致最后强测倒数三个点全部CPU_TIME_LIMIT_EXCEED。
第二次bug修复可谓是让我伤透了脑筋,问题就出在我的DFS算法上,我在DFS的一开头就new了一个二维的HashMap,然后进行了递归运算,由于第二次同时允许存在120个不同的点,如果整个图存在大量的点联通,那么相应的我的DFS方法也就会进行大量的递归运算,首先现实时间就会很慢,这一点我在和朋友的对拍中就已经发现,其次由于递归的过程中不断的new新的容器,导致好几个点都出现了CPU_TIME_LIMIT_EXCEED的报错。大概在现有算法的基础上挣扎了好几个小时之后,我最终还是选择了对程序进行重构(心态崩了),并且成功在第三次作业中沿用第二次的架构。
第三次进行强测之前我自己写了一个对拍器和朋友进行了长时间的测评和bug修复,最后在强测中获得了满分。
如果说按85分算作及格的话,那么很高兴我三次作业都在互测阶段成功的达到了目标,并且在自己扣分情况最严重的第二次互测中,把自己被扣掉的分用hack的方式挣了回来。这个单元给我最深刻的感觉就是主动去写一个好的对拍测评机是一件很高效很有用的事,花一个小时写测评机,后面的二十几个小时就只需要去做复制粘贴的工作了,何乐而不为的一件事。
八.对第三单元作业的一些感想
个人感觉第三单元相比前两个单元要友好了不少,虽然菜鸡本人在过程中也干了不少蠢事,爆了不少error,增加了一些对算法的要求,这对于OO来说应该也是必不可少的一个部分。开始这个单元之前我一直以为会要求我们自己手写JML规格,后来发现不仅写规格是一件比我想象中要复杂的多的事,就连读规格都没有那么简单(当然很有可能单纯是因为我太菜了)。不过JML语言所传递的那种追求统一的契约形式确实非常值得我们学习,在未来大三的软件工程,当我们以小组为单位进行代码书写时很可能会利用这种思路来工作。
然后是继承代码框架的部分,这个单元感觉自己做的还比较满意,尤其是第二第三次作业实现了算法的继承和扩展,基本上新增的代码都只是在做一些做基本的操作,工作变得十分轻松愉快,正确性也能得到完全的保证。
怎么说呢,每个单元都是这样,过程很辛苦,结果很快乐(测评爆零就不太快乐了),确确实实在OO每周辛苦的过程中学到了不少有用的东西,付出了总归还是会有收获。期待下个单元有更多新鲜的东西,下次OO作业见。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号