[代码随想录]Day01-数组part01

题目：704. 二分查找

思路：

二分查找一般是在有序的数组中查找指定的值，单纯的查找值，把数组跑一遍的复杂度为O(n)。

二分查找每次把范围缩小一半，我们每次都去中间的值，有以下三种情况：

1. 如果mid位置的值比target大，那么target应该在mid左侧的位置(由小到大排序情况下)
2. 如果mid位置的值比target小，那么target应该在mid右侧的位置(由小到大排序情况下)
3. 如果mid位置的值等于target，返回mid

分治的思想不断重复上述过程(for循环)直到left和right达到某种状态停止，此时如果没有返回，说明数组内没有目标值，二分的时间复杂度为O(log2N)

二分查找法一般又分为两种：左闭右闭以及左闭右开，即[left,right]以及[left,right)。

1. 当在[left,right]中查找目标值时，left=right是有意义的(理解为[1,1]是有意义的)，因此不能忽略掉。
   1. 结束条件为for left <= right；
   2. 当x[mid] < target时，mid所在位置不是目标值，left又是闭区间本身是具有意义，因此left = mid + 1 而不是left = mid；
   3. 当x[mid] > target时，mid所在位置不是目标值，right又是闭区间本身具有意义，因此right = mid - 1而不是right = mid
2. 当在[left,right)中查找目标值时，left=right无意义(理解为[1,1)是有无意义的)，因此可以忽略掉。
   1. 结束条件为for left < right；
   2. 当x[mid] < target时，mid所在位置不是目标值，left又是闭区间本身是具有意义，因此left = mid + 1 而不是left = mid；
   3. 当x[mid] > target时，mid所在位置不是目标值，同时right是开区间本身无意义，因此right = mid而不是right = mid-1(如果right = mid - 1那么mid-1就不会被查找到)

代码：

func search(nums []int, target int) int {
    left,right := 0,len(nums)
    for left < right { // 左闭右开
        mid := left + ((right - left) >> 1) // 取中间值优化版
        if nums[mid] == target { // 找到目标值返回位置
            return mid
        }
        if nums[mid] < target {  
            left = mid + 1
        }else if nums[mid] > target {
            right = mid
        }
    }
    return -1 // 没有找到值返回-1
}

补充：

有两点可以优化的地方：

1. (right + left) / 2的操作可以用位运算来进行会优化一点(right + left) >> 1。
2. right + left的操作可能会超出数据范围，因此可以left + ((right - left) >> 1)用减法再加法来避免。

参考：

文章讲解

视频讲解

题目：27. 移除元素

思路：

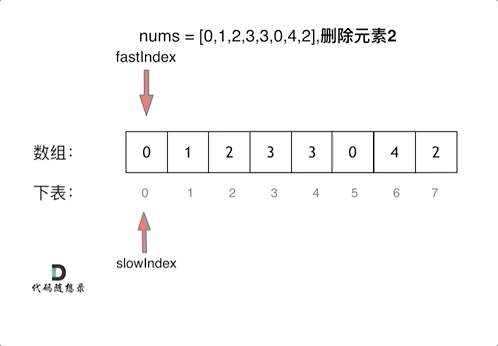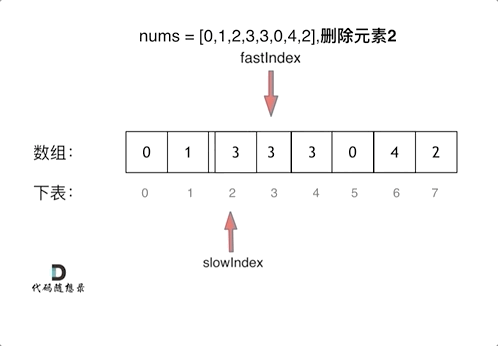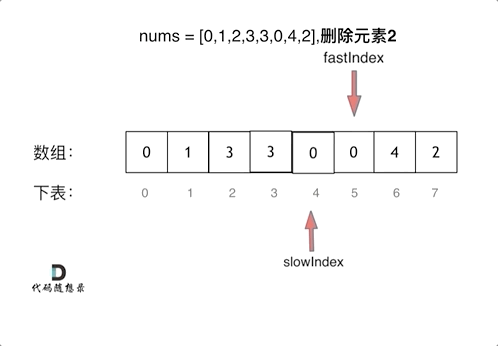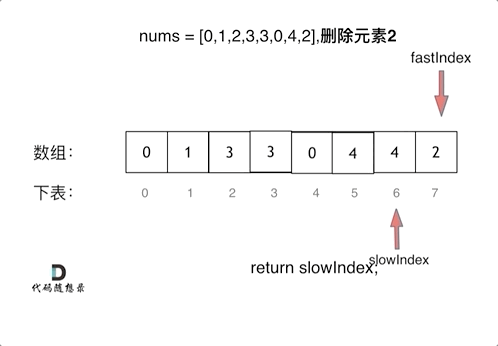
双指针法解决问题，慢指针实际上维护的是一个没有目标元素的数组(逻辑上)，而快指针是遍历先前的数组。因此当快指针遍历到目标元素时，慢指针不采取任何行动因为自己的数组中不存在该元素；当元素不是目标元素时，慢指针维护自己的数组。

因为慢指针在快指针左侧，所以不会影响到先前数组的元素，不需要担心。

代码：

func removeElement(nums []int, val int) int {
    l := 0 // 慢指针
    lens := len(nums) // 元素数量
    for r := 0; r < len(nums); r++ { // 遍历指针(快指针)
        if nums[r] == val { // 如果等于那就元素数量-1，慢指针不动
            lens--
            continue
        }
        nums[l] = nums[r] // 如果不等于把快指针的值赋给慢指针
        l++
    }
    nums = nums[:lens] // 删除多余的元素
    return lens
}

参考：

文章讲解

视频讲解

题目：34. 在排序数组中查找元素的第一个和最后一个位置

思路：

这个题其实就是考验当nums[mid] == target时该怎么处理。

找第一次出现：

1. 当nums[mid] == right，向左靠，即right = mid
2. 当边界情况left = right - 1时，因为一个奇数一个偶数，除以二一定是取小的(left)，那left不是target就会向右移动
3. 如果存在target，结束时left = right，且在第一个target处
4. 如果不存在target，结束时nums[right] != target
5. 注意right != len(nums)

找最后一次出现：

1. 当nums[mid] == right，向右靠，即left = mid - 1
2. 当边界情况left = right - 1时，因为一个奇数一个偶数，除以二一定是取小的(left)，那left不是target就会向右移动
3. 如果存在target，结束时left = right，且在最后一个target+1处
4. 如果不存在target，结束时nums[left - 1] != target
5. 注意left != 0

代码：

func searchRange(nums []int, target int) []int {
    if len(nums) == 0 { // 没有元素直接返回-1，-1
        return []int{-1,-1}
    }
    return []int{FindStart(nums, target),FindEnd(nums, target)}
}

func FindStart(nums[]int,target int)int {
    left, right := 0 , len(nums) 
    for left < right {
        mid := left + ((right - left) >> 1)
        if nums[mid] < target {
            left = mid + 1
        }else { // 处理nums[mid] = target
            right = mid
        }
    }
    if right != len(nums) && nums[right] == target { // 注意不要越界right位置是不是？
        return right
    }
    return -1
}

func FindEnd(nums[]int,target int) int{
    left, right := 0 , len(nums)
    for left < right {
        mid := left + ((right - left) >> 1)
        if nums[mid] > target {
            right = mid
        }else { // 处理nums[mid] = target
            left = mid + 1
        }
    }
    if left != 0 && nums[left - 1] == target { // 注意不要越界left-1位置是不是？
        return left - 1
    }
    return -1
}

题目：35. 搜索插入位置

思路：

其实就是普通的二分，需要考虑到的是停止位置就是插入位置。

代码：

func searchInsert(nums []int, target int) int {
    left, right := 0, len(nums)
    for left < right {
        mid := left + ((right - left) >> 1)
        if target < nums[mid] {
            right = mid
        } else if target > nums[mid] {
            left = mid + 1
        }else {
            return mid
        }
    }
    return right
}