数据结构与算法

软件需求分析与系统设计	https://edu.cnblogs.com/campus/zswxy/2018SE
这个作业要求在哪里	https://edu.cnblogs.com/campus/zswxy/2018SE/homework/11406
这个作业的目标	排序算法与二叉树遍历
参考资料	尚硅谷 Java数据结构与Java算法

基本学习：

尚硅谷 Java数据结构与Java算法

冒泡排序算法：

• 基本思想：
  通过对待排序序列从前向后（从小标较小的元素开始），依次比较相邻的值，若发现逆序则交换，使较大的元素逐渐从前向后移。
  因为排序的过程中，各元素不断接近自己的位置，如果一趟比较下来没有进行过交换，就说明序列有序，
  因此在排序过程中设置一个flag判断是否交换。从而减少不必要的比较
  
  小结：(1)一共进行数组的大小-1次大的循环
  (2) 每一趟排序的次数在逐渐的减少
  (3)如果发现某一趟排序中，没有发生一次交换，可以提前结束冒泡排序。

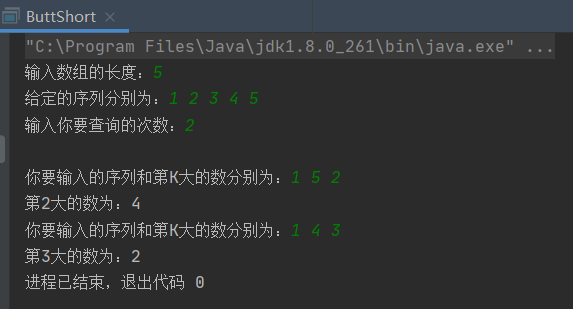
题一、寻找数组中第K大是数 考察算法：排序算法

1.1实现：冒泡排序算法

1.2基本思路：

1、分析题意
2、调用Scanner()方法实现序列的输入
3、遍历输入的序列，存入数组
4、确定输入次数，使用循环确定序列首尾和第K大数
5、使用冒泡排序算法实现找到对应的第K大数
6、输出结果

1.3代码实现：

'''java

    package com.company;

  import java.util.ArrayList;

  import java.util.Scanner;

  /**
   * 给定一个序列，每次询问序列中第i个数到第r个数中的第K大的数是那个
   */
  public class ButtShort {
       public static void main(String[] args) {

         Scanner input = new Scanner(System.in);
         System.out.print("输入数组的长度：");
         int n = input.nextInt();
         System.out.print("给定的序列分别为：");
          int[] arr1 = new int[n + 1];

    for (int i = 1; i <= n; i++) {  //遍历数组各元素
        arr1[i] = input.nextInt();

        /*检查遍历序列
        System.out.print(arr[i]);

         */
    }
    System.out.print("输入你要查询的次数：");

        int m = input.nextInt();
        int[] arr2 = new int[n + 1];
        int temp; //临时变量
        boolean flag = false; // 标识变量，表示是否进行过交换

        for (int i = 1; i <= m; i++) {
            System.out.print("\n你要输入的序列和第K大的数分别为：");

            for (int j = 1; j <= n; j++) {
                arr2[j] = arr1[j];
            }

            int l = input.nextInt();  //序列首
            int r = input.nextInt();  //序列位
            int k = input.nextInt();   // 第K大的数

            //冒泡排序，时间复杂度O(N²)
            for (int a = 1; a <= r; a++) {
                for (int b = a; b <= r; b++) {
                    if (arr2[b] > arr2[a]) {
                   //   flag = true;
                        temp = arr2[b];
                        arr2[b] = arr2[a];
                        arr2[a] = temp;
                    }

                }
            /*
                if (!flag) {  //如果没有交换，就退出
                    break;
                } else {
                    flag = false; //重置flag,进行下次交换。
                }
                
            */
            }

            System.out.print("第" + k + "大的数为：" + arr2[1 + k - 1]);
        }



   }
}

'''

1.4运行结果

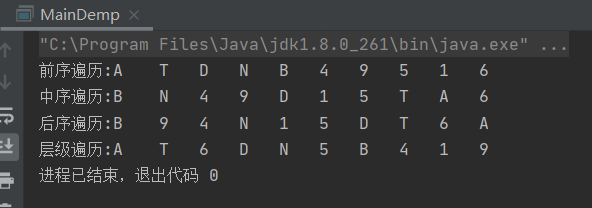
题二、二叉树的先、中、后 序遍历与层级遍历 考察算法： dfs + bfs搜索算法

1.1实现：递归算法

1.2基本思路：

• 创建一颗二叉树
• 前序遍历：先输出父节点，在遍历左子树和右子树
  • 先输出当前节点（初始root节点）；
  • 如果左子节点不为空则递归继续前序遍历；
  • 如果右子节点不为空则递归继续前序遍历
• 中序遍历：先遍历左子树，在输出父节点，再遍历右子树
  • 先输出当前节点左子节点不为空，则递归中序遍历；
  • 输出当前结点；
  • 如果当前右子节点不为空，则递归继续中序遍
• 后序遍历：先遍历左子树，再遍历右子树，最后输出父节点
  • 如果当前节点左子节点不为空，则递归后序遍历；
  • 如果当前右子节点不为空，则递归继续后序遍历；
  • 输出当前结点
• 层级遍历：每一层从左到右遍历，借助队列实现。

1.3代码实现：

'''java

   package com.company;

    /**
       作业要求：叉树的先、中、后 序遍历与层级遍历
       自己实现四个方法，main方法中调用，将结果打印到控制台
    */

     import java.util.LinkedList;

    /**  二叉树的结构
                 A
                / \
               T   6
              /
             D
           /   \
          N     5
         / \    /
        B   4  1
             \
              9

      */
 public class MainDemp {


   public static void main(String[] args) {

    Info info = new Info();

    Node root = new Node("A");
    Node node1 = new Node("T");
    Node node2 = new Node("D");
    Node node3 = new Node("N");
    Node node4 = new Node("B");
    Node node5 = new Node("6");
    Node node6 = new Node("5");
    Node node7 = new Node("4");
    Node node8 = new Node("9");
    Node node9 = new Node("1");

    //说明，手动创建二叉树
    root.setL(node1);
    node1.setL(node2);
    node2.setL(node3);
    node2.setR(node6);
    node3.setR(node7);
    node7.setR(node8);
    node6.setL(node9);
    node3.setL(node4);
    root.setR(node5);
    info.setRoot(root);

    //测试，前序遍历
    System.out.print("前序遍历:");
    info.A();

    //中序遍历
    System.out.print("\n中序遍历:");
    info.B();


    //后序遍历
    System.out.print("\n后序遍历:");
    info.C();

    //层级序列
    System.out.print("\n层级遍历:");
    info.D();




    }

 }

   class Info{
          private Node root;

      public void setRoot(Node root) {
           this.root = root;
    }

    //前序遍历
    public void A(){
        if (this.root != null){
            this.root.A();
        }else {
            System.out.print("当前二叉树为空，无法遍历");
        }
    }

    //中序遍历
    public void B(){
        if (this.root != null){
            this.root.B();
        }else{
            System.out.print("当前二叉树为空，无法遍历");
        }
    }

    //后序遍历
    public void C(){
        if (this.root != null){
            this.root.C();
        }else{
            System.out.print("当前二叉树为空，无法遍历");
        }
    }

    public void D(){
        if (this.root != null){
            this.root.D();
        }else{
            System.out.print("当前二叉树为空，无法遍历");
        }
    }
 }

     // 节点
 class Node {
      // 数据
      private String data;
      // 左孩子
      private Node l;
      // 右孩子
      private Node r;


    public Node(String data) {
        this.data = data;

    }

    public String getData() {
        return data;
    }

    public void setData(String data) {
        this.data = data;
    }

    public Node getL() {
        return l;
    }

    public void setL(Node l) {
        this.l = l;
    }

    public Node getR() {
        return r;
    }

    public void setR(Node r) {
        this.r = r;
    }

    @Override
    public String toString() {
        return  data ;
    }

    public void A() {
        // TODO 先序遍历
        System.out.print(this + "\t"); //先输出父节点
        //递归前序左子树前序遍历
        if (this.l != null) {
            this.l.A();
        }
        //递归右子树遍历
        if (this.r != null) {
            this.r.A();
        }
    }

    public void B() {
        // TODO 中序遍历
        //递归向左子树中序遍历
        if (this.l != null) {
            this.l.B();
        }
        //输出父节点
        System.out.print(this + "\t");
        //递归右子树中序遍历
        if (this.r != null) {
            this.r.B();
        }
    }

    public void C() {
        // TODO 后续遍历
        if (this.l != null) {
            this.l.C();
        }
        if (this.r != null) {
            this.r.C();
        }
        System.out.print(this + "\t");
    }

    public void D() {

        // TODO 层级遍历

        if (this == null){
            return;
        }
        LinkedList<Node> queue = new LinkedList<>();
        Node current = null;
        queue.offer(this);
        while (!queue.isEmpty()){
            current = queue.poll();
            System.out.print(current.data + "\t");
            if (current.l != null){
                queue.offer(current.l);
            }
            if(current.r != null) {//如果当前节点的右节点不为空，把右节点入队
                queue.offer(current.r);
            }
        }

    }
}

'''

2.4运行结果