二维前缀和
二维前缀和入门：
\(我们DP来预处理，dp\left [ i\right ]\left [ j\right ]表示\left ( 1,1\right )这个点与\left ( i,j\right )这个点两个点分别为左上角和右下角所组成的矩阵内的数的和，转移方程:\)
\(dp\left [ i\right ]\left [ j\right ]=dp\left [i-1 \right ]\left [j \right ]+dp\left [ i\right ]\left [ j-1\right ]-dp\left [ i-1\right ]\left [ j-1\right ]+mp\left [ i\right ]\left [ j\right ]\left ( mp\left [ i\right ]\left [ j\right ]表示二维表格\left ( i,j\right )处的值\right )\)
预处理完毕，下面来讲怎么快速的得出我们想要的任意子矩阵中的和，我们定义\(\left ( x_{1},y_{1}\right )为我们想要的子矩阵的左上角，\left ( x_{2},y_{2}\right )为我们想要的子矩阵的右下角\)
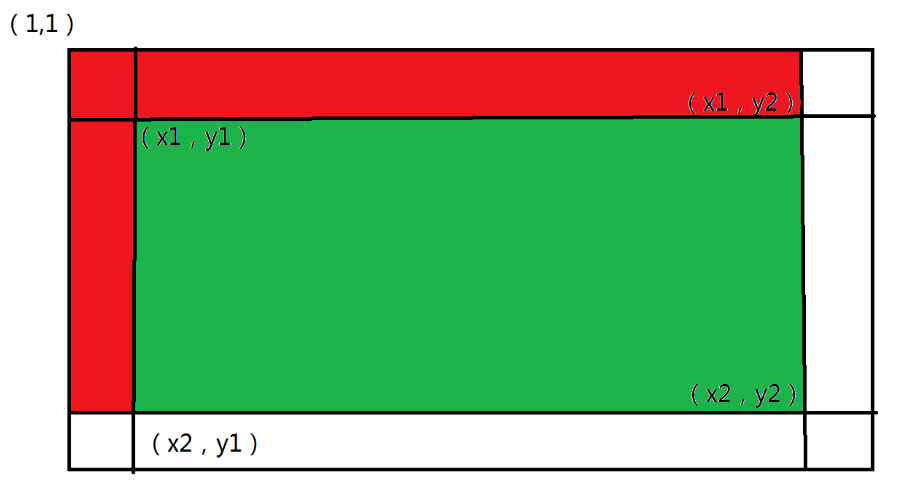
那么由图可得，\(dp\left [ x_{2}\right ]\left [ y_{2}\right ]-dp\left [ x_{1}-1\right ]\left [ y_{2}\right ]-dp\left [ x_{2}\right ]\left [ y_{1}-1\right ]+dp\left [ x_{1}-1\right ]\left [ y_{1}-1\right ]\)
模板代码：
1 #include <bits/stdc++.h> 2 using namespace std; 3 #define endl '\n' 4 typedef long long ll; 5 const int maxn = 1e3+10; 6 const int inf = 0x3f3f3f3f; 7 const ll mod=1e9+7; 8 9 int dp[maxn][maxn],mp[maxn][maxn]; 10 int n,m,k; 11 int main() 12 { 13 ios::sync_with_stdio(false); 14 cin>>n>>m>>k; 15 for(int i=1;i<=n;i++) 16 for(int j=1;j<=m;j++) 17 cin>>mp[i][j]; 18 19 memset(dp,0,sizeof(dp)); 20 for(int i=1;i<=n;i++) 21 for(int j=1;j<=m;j++) 22 dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mp[i][j]; 23 24 for(int i=1;i<=k;i++){ 25 int x1,y1,x2,y2; 26 cin>>x1>>y1>>x2>>y2; 27 int ans=dp[x2][y2]-dp[x2][y1-1]-dp[x1-1][y2]+dp[x1-1][y1-1]; 28 cout<<ans<<endl; 29 } 30 return 0; 31 }
本博客图来自于：here
