并查集 按秩合并&路径压缩

并查集

一种可以动态维护若干个不重叠的集合或无向图的连通块的数据结构。

主要支持以下操作：

find : 查询一个元素属于哪个集合

merge : 合并两个集合

并查集的每个集合都需要一个“爹”来表示这整个集合，所以判断两个元素是否在同一集合，就看他们爹是否相同。

有一个显而易见的初始化，对于要维护的序列，初始每个元素的爹就是他自己，也就是初始化。

inline void init(int n){
    for(int i=1;i<=n;++i)fa[i] = i;
}

这里直接放上找爹函数，也就是 find 操作，递归完成

inline int findfa(int x){
    return fa[x] == x ? x : fa[x] = findfa(fa[x]);
}

路径压缩

考虑这样的情况

 

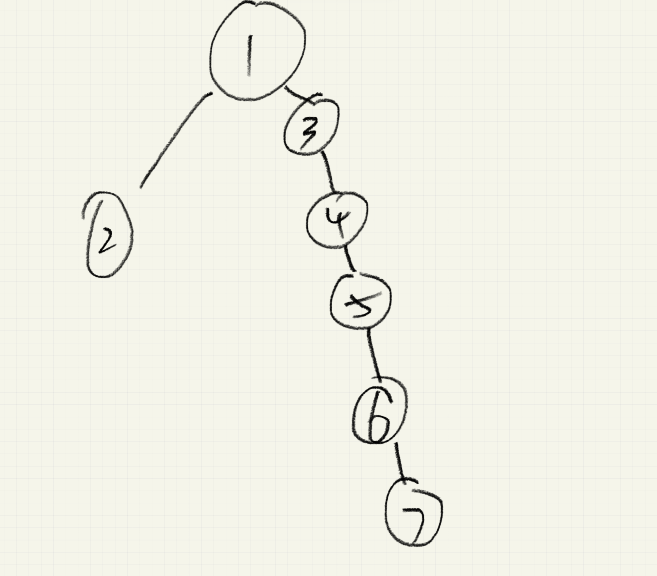
画的好丑

 

是不是在找 $7$ 的爹的时候要好久好久，这显然是不能接受的。

这就要用到路径压缩了，怎么压呢？

 

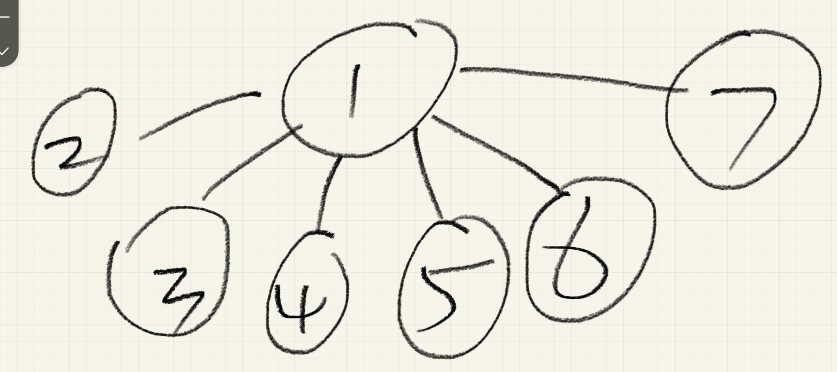
 相信聪明的你已经明白了

我们在合并的时候直接连到爹上去，顺便查找的时候也直接连上去，就OK啦。

也就是说

fa[findfa(x)] = findfa(y);

按秩合并

 我们把每个集合看成一个树，记录一个 $siz$数组维护树的深度，每次将深度小的合并到深度大的，这样可以保证树的最大深度为 $logn$ 这种方法不会破坏树的结构，对于以后学习的撤销操作和可持久化有益。。

 

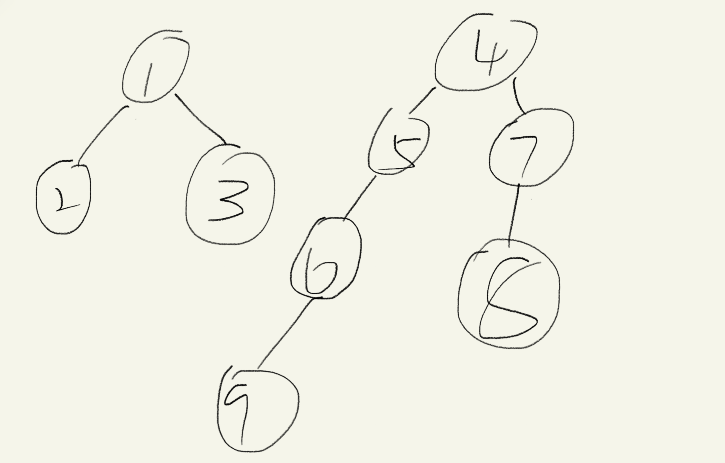
 观察这两颗树，显然将$1$接到$4$下面，树的深度不会增大，但将$4$接到$1$下面，树却变深。

 

当然了，按秩合并顺便路径压缩也是可以的，并且很快

inline void merge(int x,int y){
    int u = findfa(x),v = findfa(y);
    if(u == v)return;
    if(siz[u] > siz[v])fa[v] = u;
    else{
        if(siz[u] == siz[v])siz[v]++;
        fa[u] = v;
    }
}

 

初始的时候 $siz$ 都为 $1$ 。