1.5 带符号数表示法
1.5 带符号数表示法
原码、反码、补码带上符号位均为8位
-
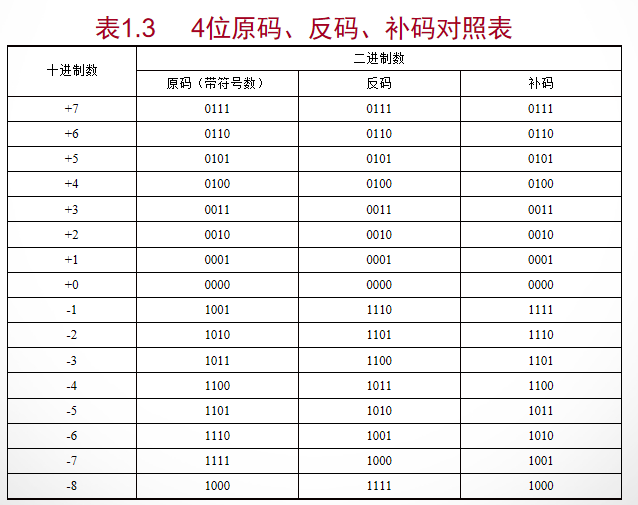
原码表示法
原码(True Form)表示法是在二进制数值之前加一个符号位。通常用0表示正数,用1表示负数,后面的数位表示数的大小。
例:分别写出 (+11)10 和 (-11)10 的8位二进制原码。![image-20210903174858521]()
![image-20210903174909722]()
-
反码表示法
反码(One's Complement)表示法的符号位表示与原码相同,数值位表示的规则如下:对于正数,其数值位与原码表示法中相同;对于负数,除符号位以外,其余各位取反就得到了数值位。
例:分别写出 (+11)10 和 (-11)10 的8位二进制反码。(+11)10 = (+1011)2 = (+0001011)2 = (00001011)反码
(- 11)10 = (- 1011)2 = (-0001011)2 = (11110100)反码 -
补码表示法
计算机中通常采用的带符号数表示法是补码(Complement)表示法,其规则:对于正数,补码与原码相同;对于负数,符号位仍为1,二进制数值位要按位取反,然后末位加1。也就是在反码的基础上加1。
例:分别写出 (+11)10 和 (-11)10 的8位二进制补码。
(+11)10 = (+1011)2 = (+0001011)2 = (00001011)反码 = (00001011)补码
(- 11)10 = (- 1011)2 = (-0001011)2 = (11110100)反码 = (11110101)补码需要指出,当带符号数为纯小数时,原码或补码的符号位在小数点的前面,原来小数点前面的0不再表示出来。
例:分别计算 (0.01101)2 和 (- 0.01101)2 的8位二进制原码、反码和补码。
(0.01101)2 = (0.0110100)原码 = (0.0110100)反码 = (0.0110100)补码
(-0.01101)2 = (1.0110100)原码 = (1.1001011)反码 = (1.1001100)补码 -
带符号数的补码运算
利用补码,可以方便地进行带符号数的加、减运算。运算过程中需要注意的是,同号相加或异号相减时,有可能发生溢出(Overflow)。溢出是指运算结果超出了原制定位数所能表示的带符号数范围。发生溢出时需要增加二进制补码的位数。![image-20211008171727923]()

采用补码加法运算时,运算结果仍为补码。对于字长为8位的运算器,只保留8位运算结果,最高位向上的进位“1”自动丢失。当结果的符号位为0时,结果为正,否则,结果为负。

不同符号的反码相加,如果发生溢出,最高位上的进位1自动丢失
相同符号位的反码相加,如果发生溢出,只能增加补码的位数


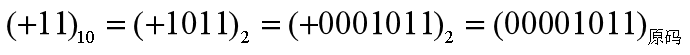
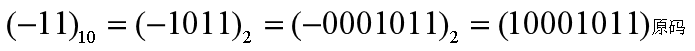


 浙公网安备 33010602011771号
浙公网安备 33010602011771号