堆排序
引入:
堆排序是一种就地算法,算法最坏时间复杂度为O(nlogn)
算法设计技术:以堆(heap)来加速,优先级队列,ADT
要想知道什么是堆排序,必须先了解堆,下面开始介绍堆:
二叉堆:是一颗完全/完整二叉树
1.结点编号从1开始的堆
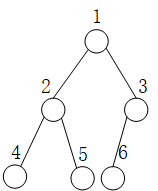
完全二叉树(结点i)

非完全二叉树
父亲 i/2 左孩子 2i 右孩子2i + 1 (比较简洁)
2. 结点编号从0开始
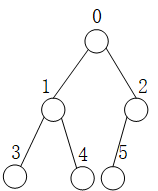
父亲 (i-1)/2 左孩子 2i + 1 右孩子2i + 2 (稍微复杂点)
数组形态 隐式堆
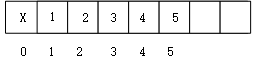
最大堆(大根堆)/最小堆(小根堆)
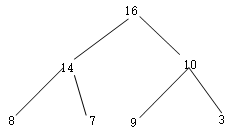
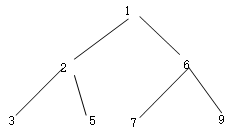
最大堆(大根堆)
大根堆的特性:
- A[i/2] >= A[i] 最大堆(大根堆)
- i/2为结点i的父亲
- 堆顶/最大元素
- 似乱非乱 完美的混乱
最小堆(小根堆)
小根堆的特性:
- A[i/2] <= A[i] 最小堆(小根堆)
- i/2为结点i的父亲
- 堆顶/最小元素
二叉堆的操作:
- 调整结点i使之满足堆特性O(logn)
- 建堆O(n)
- 堆排序O(nlogn)
- 插入元素O(logn)
- 取出最大元素O(logn)
- 对结点i升权O(logn)
- 最大元O(1)
维护堆特性
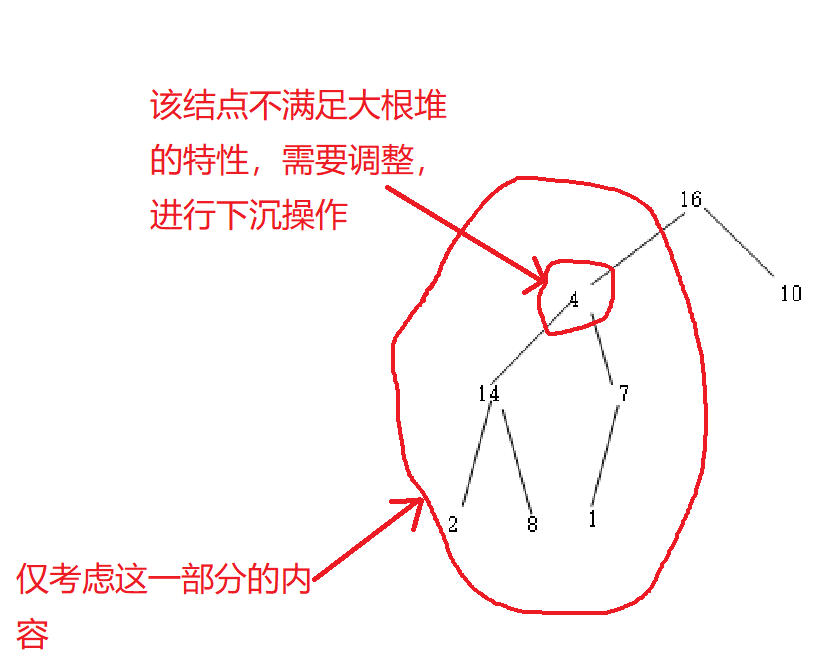
结点i的下沉 其他结点都满足要求(堆的特性)
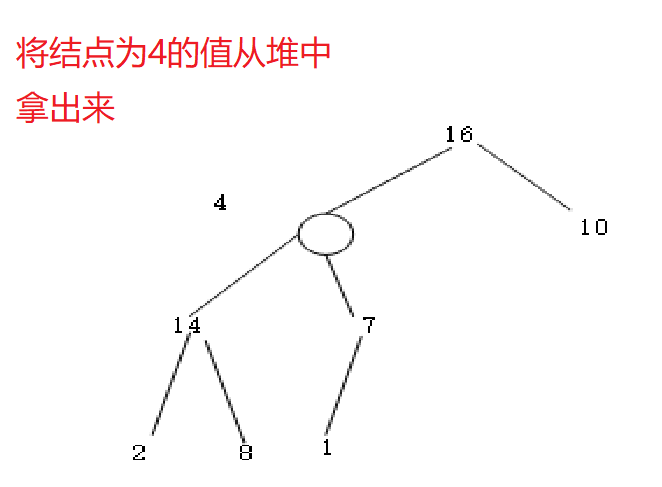
1.将结点为4的值从堆中拿出来
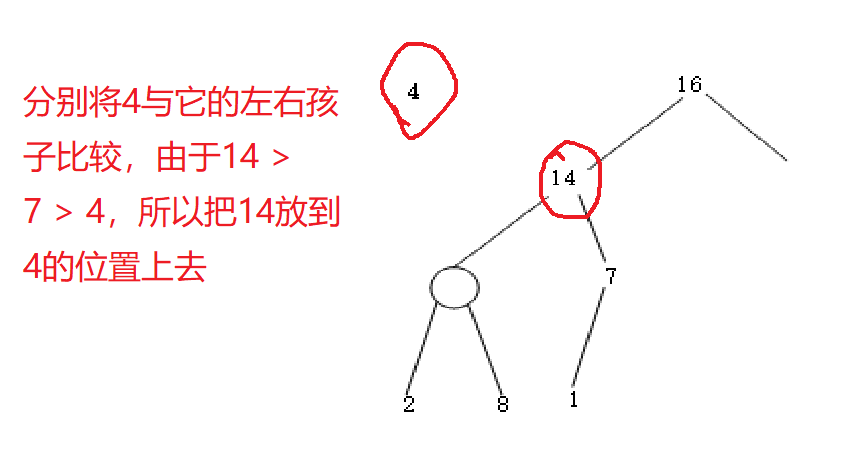
2.分别将4与它的左右孩子比较,由于14 > 7 > 4,所以把14放到4的位置上去
3.继续与原来14位置左右孩子比较,由于8 > 4 > 2,所以把8放到原来14的位置,把4放到原来8的位置
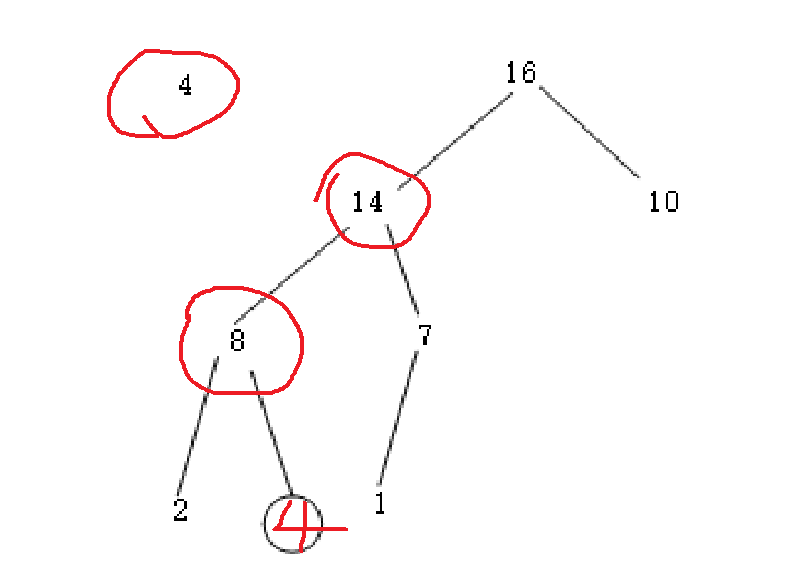
A 数组/向量 n + 1(n个元素) A[0]哨兵
/***
* 下沉操作
*/
A[0] = A[i];
size_t R = 2 * i + 1;
//1.循环中处理的是左右孩子都存在的情况下
while(R < A.size()){
size_t MAX = i;
if(A[MAX] < A[R]){
MAX = R;
}
if(A[MAX] < A[R - 1]){
MAX = R - 1;
}
if(MAX == i)
break;
A[i] = A[MAX];
i = MAX;
R = 2 * i + 1;
}
//不存在右孩子的情况
if(R == A.size() && A[i] < A[R - 1]){ //短路表达式
A[i] = A[R - 1];
i = R - 1;
}
A[i] = A[0];
堆高度至多为O(logn),所以结点至多下沉O(logn)次,所以结点下沉的时间复杂度为O(logn)
主定理:T(n) <= T(2n/3) + O(1)
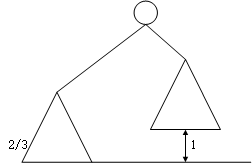
另一种表述 堆高度h 运行时间O(h)
练习:<27,17,3,16,13,10,1,5,7,12,4,8,9,0>
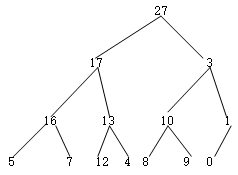
1.建堆
Floyd算法 自底向上调整 <4,1,3,2,16,9,10,14,8,7>(数组/向量)
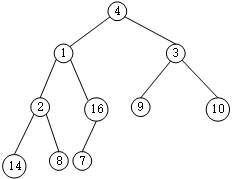
高为h,至多有个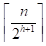 结点,调整它们要O(h)时间
结点,调整它们要O(h)时间
n个结点堆高不超过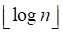 ,
,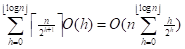
,


 浙公网安备 33010602011771号
浙公网安备 33010602011771号