Luogu P1600 [NOIP2016 提高组] 天天爱跑步
题链
[P1600 NOIP2016 提高组] 天天爱跑步 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
分析
肯定需要枚举的是观察员
感觉像换根DP,所以想换根DP一样做,分成从上到下和从下到上两部分
设路径是\((s,l,t)\)
-
从下往上(s,l),设观察员为u
\[d[s]=w[u]+d[u] \] -
从上往下(l,t)
\[Len[s,t]-d[t]+n=w[u]-d[u]+n \]
所以可以树上差分后线段树合并\(O(nlgn)\)
但是有\(O(n)\)的做法:
- 首先求LCA用tarjan
- 然后变成了在某节点对某权值进行变化,然后求子树中这些操作后某权值的大小
- 这可以利用差分
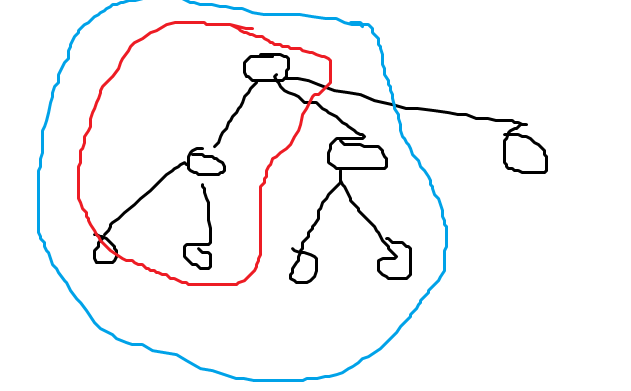
- 这可以利用差分
求这颗子树的所有权值的变化相当于蓝色区域减去红色区域
所以这个点的答案是DFS出这个点时的权值减去DFS到这个点时的权值,妙啊
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m,lg[N],f[N][20],d[N],ans[N],w[N],t1[N<<1],t2[N<<1];
vector<int>V[N];
struct A{int v,w; };
vector<A>V1[N],V2[N];
void dfs(int fa,int u) {
d[u]=!fa?0:d[fa]+1;
f[u][0]=fa;
for(int i=1;i<=lg[d[u]];i++) {
f[u][i]=f[f[u][i-1]][i-1];
}
for(int v:V[u]) {
if(v!=fa) dfs(u,v);
}
}
inline int lca(int u,int v) {
if(d[u]>d[v]) swap(u,v);
while(d[u]<d[v]) v=f[v][lg[d[v]-d[u]]];
if(u==v) return u;
for(int i=lg[d[u]];i>=0;i--) {
if(f[u][i]!=f[v][i]) {
u=f[u][i],v=f[v][i];
}
}
return f[u][0];
}
void dgs(int fa,int u) {
if(w[u]+d[u]<=n) ans[u]-=t1[w[u]+d[u]];
ans[u]-=t2[w[u]-d[u]+n];
for(A v:V1[u]) {
t1[v.v]+=v.w;
}
for(A v:V2[u]) {
t2[v.v+n]+=v.w;
}
for(int v:V[u]) {
if(v!=fa) {
dgs(u,v);
}
}
if(w[u]+d[u]<=n) ans[u]+=t1[w[u]+d[u]];
ans[u]+=t2[w[u]-d[u]+n];
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<n;i++) {
int u,v; scanf("%d%d",&u,&v);
V[u].push_back(v),V[v].push_back(u);
}
lg[0]=-1;
for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
dfs(0,1);
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
for(int i=1;i<=m;i++) {
int u,v; scanf("%d%d",&u,&v);
int l=lca(u,v),len=d[u]+d[v]-d[l]-d[l];
V1[u].push_back((A){d[u],1});
V1[f[l][0]].push_back((A){d[u],-1});
if(v!=l) {
V2[v].push_back((A){len-d[v],1});
V2[l].push_back((A){len-d[v],-1});
}
}
dgs(0,1);
for(int i=1;i<=n;i++) {
printf("%d%c",ans[i],i==n?'\n':' ');
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号