长链剖分

基槽：

优化转移时间复杂度只和深度有关的树形DP

思想：

定义重儿子为深度最大的儿子，每次巧妙地利用数组分配空间的方式(利用dfn序)继承来自重儿子的信息，然后暴力合并亲儿子，均摊时空复杂度\(O(n)\)。

Pf：定义长链为最长的全是由重儿子组成的链，则长链的顶点一定是一个轻儿子,对于每个点，只存在于一条长链上，每条长链只会合并一次，需要深度大小的时间，合并后根节点的深度不会发生变化。

所以可以大胆地把时间均摊到每个节点，均摊\(O(1)\).

Luogu P3565 [POI2014]HOT-Hotels

显然3个点不可能在一条链上，只可能是（先找两个点）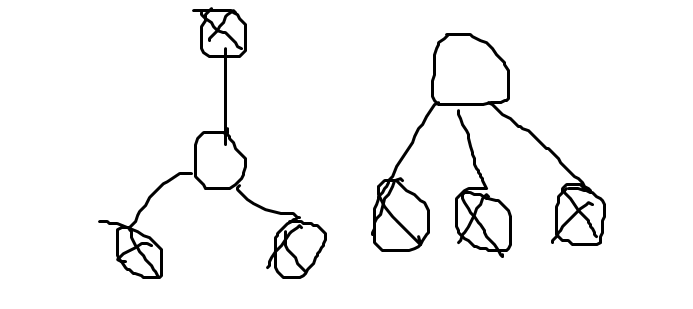

第二种情况好弄，第一种情况本能想到换根，但由于每次和深度有关，所以无法换根DP

\(f[u][i]\)表示\(u\)的子树中深度为\(i\)的节点个数

正难则反，之所以无法换根DP是因为无法维护fa的深度数组，所以考虑维护\(g[u][i]\)表示u的子树中还需要\(i\)的距离的点对数量即可

void dgs(int fa,int u) {
    f[u][1]=1;
    for(int e=he[u];e;e=nxt[e]) {
        int v=to[e];
        if(v!=fa) {
            dgs(u,v);
            for(int i=0;i<=dep[v];i++) {
                if(i) ans+=(ll)f[u][i-1]*g[v][i];
                ans+=(ll)g[u][i+1]*f[v][i];
            }
            for(int i=1;i<=dep[v]+1;i++) {
                g[u][i]+=g[v][i+1]+(ll)f[u][i]*f[v][i-1];
                f[u][i]+=f[v][i-1];
            }
        }
    }
    ans+=g[u][0];
}

长链剖分（此为无dfn序版本）

#include<bits/stdc++.h>
#define ll long long
using namespace std;

const int N=1e5+5;
int n,cnt,id,to[N],nxt[N],he[N],son[N],dep[N],sf[N],sg[N];
ll t[N],ans;


inline void add(int u,int v) {
    to[++cnt]=v,nxt[cnt]=he[u],he[u]=cnt;
}

void dfs(int fa,int u) {
    for(int e=he[u];e;e=nxt[e]) {
        int v=to[e];
        if(v!=fa) {
            dfs(u,v); 
            if(dep[v]>dep[son[u]]) son[u]=v;
        }
    }
    dep[u]=dep[son[u]]+1;
}

void dgs(int fa,int u) {
    if(son[u]) {
        sf[son[u]]=sf[u]+1,sg[son[u]]=sg[u]-1;
        dgs(u,son[u]);
        ans+=t[sg[u]];
    }
    t[sf[u]]=1;
    for(int e=he[u];e;e=nxt[e]) {
        int v=to[e];
        if(v!=fa&&v!=son[u]) {
            sf[v]=id,id+=(dep[v]<<1); sg[v]=id; id+=(dep[v]<<1);
            dgs(u,v);
            for(int i=0;i<=dep[v];i++) {
                if(i) ans+=(ll)t[sf[u]+i-1]*t[sg[v]+i];
                ans+=(ll)t[sg[u]+i+1]*t[sf[v]+i];
            }
            for(int i=0;i<dep[v];i++) {
                t[sg[u]+i]+=(ll)t[sg[v]+i+1];
            }
            for(int i=1;i<=dep[v]+1;i++) {
                t[sg[u]+i]+=(ll)t[sf[u]+i]*t[sf[v]+i-1];
                t[sf[u]+i]+=t[sf[v]+i-1];
            }
        }
    }
}

int main() {
    scanf("%d",&n);
    for(int i=1;i<n;i++) {
        int u,v; scanf("%d%d",&u,&v);
        add(u,v),add(v,u);
    }
    dfs(0,1);
    sf[1]=id; id+=(dep[1]<<1); sg[1]=id; id+=(dep[1]<<1);
    dgs(0,1);
    printf("%lld\n",ans);
    return 0;
} 

例题2

题链
显然，每个人独立，答案均为n个点中选x个点的答案

\[ S =\sum_{(u,v) \in E}[(u,v)\in M]\frac{C(x-2,n-2)}{C(x,n)}=\sum_{(u,v) \in E}[(u,v)\in M]\frac{x(x-1)}{n(n-1)}=\frac{x(x-1)}{n(n-1)}\sum_{(u,v) \in E}[(u,v)\in M] \]

#include<bits/stdc++.h>
#define ll long long
#define db long double
using namespace std;

const int N=5e4+5;
int to[N<<1],nxt[N<<1],he[N],cnt,n,m,a[N],d[N],son[N],mx[N],L[N];
ll ans;

inline void add(int u,int v) {
	to[++cnt]=v,nxt[cnt]=he[u],he[u]=cnt;
}

void dfs(int fa,int u) {
	son[u]=0; mx[u]=0;
	for(int e=he[u];e;e=nxt[e]) {
		int v=to[e];
		if(v!=fa) {
			dfs(u,v);
			if(mx[v]+1>mx[u]) {
				mx[u]=mx[v]+1;
				son[u]=v;
			}
		}
	}
}

void dgs(int fa,int u) {
	L[u]=++cnt; d[L[u]]=1;
	if(son[u]) dgs(u,son[u]);
	for(int i=1;i<=m;i++) {
		if(a[i]<=mx[u]) ans+=d[L[u]+a[i]];
	}
	for(int e=he[u];e;e=nxt[e]) {
		int v=to[e];
		if(v!=fa&&v!=son[u]) {
			dgs(u,v);
			for(int i=1;i<=m;i++) {
				for(int j=max(a[i]-mx[u]-1,0);j<=min(a[i]-1,mx[v]);j++) {
					ans+=(ll)d[L[v]+j]*d[L[u]+a[i]-j-1];
				}
			}
			for(int i=0;i<=mx[v];i++) d[L[u]+i+1]+=d[L[v]+i];
		}
	}
}
int main() {
	freopen("game.in","r",stdin);
	freopen("game.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++) scanf("%d",&a[i]);
	for(int i=1;i<n;i++) {
		int u,v; scanf("%d%d",&u,&v);
		add(u,v),add(v,u);
	}
	cnt=0;
	dfs(0,1),dgs(0,1);
	if(n%3==0) {
		db Ans=(db)ans/9/(n-1)*(n-3);
		printf("%.2Lf\n%.2Lf\n%.2Lf\n",Ans,Ans,Ans);
	}
	if(n%3==1) {
		db Ans1=(db)ans/n/(n-1)*(n/3+1)*(n/3),Ans2=(db)ans/n/(n-1)*(n/3-1)*(n/3);
		printf("%.2Lf\n%.2Lf\n%.2Lf\n",Ans1,Ans2,Ans2);
	}
	if(n%3==2) {
		db Ans1=(db)ans/n/(n-1)*(n/3+1)*(n/3),Ans2=(db)ans/n/(n-1)*(n/3-1)*(n/3);
		printf("%.2Lf\n%.2Lf\n%.2Lf\n",Ans1,Ans1,Ans2);
	}
	return 0;
}