虚树

分析

将树压缩成若干所需要的节点构成的树

卿，这边建议用namespace偶

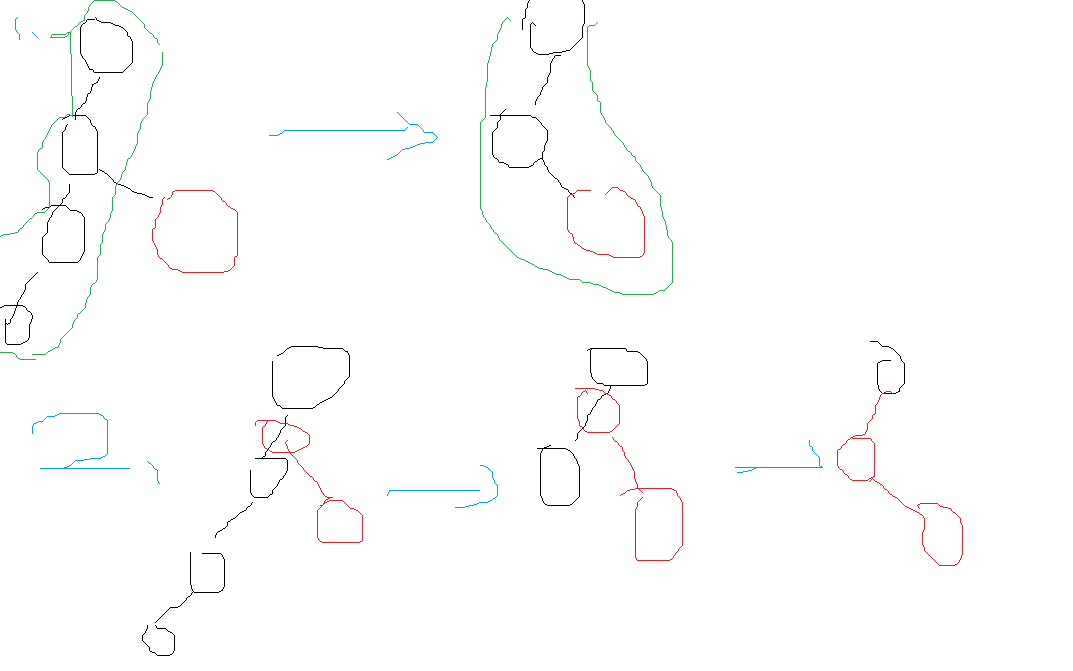
构造方法：每次取出需要的点，按dfs序排序，维护一条链，加入lca和点，每当有点出链时加边

一图流：（画了坨屎，请见谅）

sort(a+1,a+cnt+1,cmp);
st[++top]=a[1];	
for(int i=2;i<=cnt;i++) {
		int l=LCA::lca(a[i],st[top]); b[l]=1;
		for(;top>1&&dfn[st[top-1]]>=dfn[l];top--) {
			E[st[top-1]].pb(st[top]);
		}
		if(dfn[st[top]]>dfn[l]) {
 			E[l].pb(st[top]);
 			top--;
		}
		if(l!=st[top]) st[++top]=l;
		st[++top]=a[i];
	}
	for(;top>1;top--) {
		E[st[top-1]].pb(st[top]);
	}

秘诀

虚树上有5类点

第一类：节点
第二类：节点子树中的点（子树中不存在虚点）
第三类：链上的节点
第四类：链节点的子树中的点（子树中不存在虚点）
第五类：根上方的点

在计算是不要落下任何一类，否则打对拍吧

PS：不存在两个在虚树上的点之间LCA不在虚树上，也就是不存在交叉的链

例题1

Luogu P3233 [HNOI2014]世界树

首先：被一个点管辖的点呈现块状~~（屁话）~~

显然需要虚树

考虑如何快速求出一个点能管辖到的点，这有亿点难

所以思考如何快速求出虚树上某个点被哪个点管辖，也就是以这个点为根是哪个点距离最近（距离，因为在虚树上），换根DP

分成儿子和父亲上方两部分，儿子中一遍DFS，父亲上方再一遍DFS（不需要剔除自己，因为自己到父亲再到自己是劣于直接到自己的）

在虚树上，导致节点被压缩了，所以需要分配节点，考虑5类点：

第一类：节点——已经求出
第二类：节点子树中的点——显然归节点管
第三类：路径——如果两头都归某个节点管，则整条路径都在上面，否则必然是在某条边上截断（列个方程求出点的位置）
第四类：路径子树上的节点：倍增计算
第五类：根上方的节点——显然归根管

就莫得了

#include<bits/stdc++.h>
const int INF=1e8;
using namespace std;

inline int rd() {
	int ret=0; char ch=getchar();
	while(!isdigit(ch)) ch=getchar();
	for(;isdigit(ch);ch=getchar()) ret=(ret<<1)+(ret<<3)+ch-'0';
	return ret;
}

const int N=3e5+5;
int n,m,dfn[N],a[N],top,st[N],ans[N],sz[N],fid[N],SZ[N];
vector<int>V[N];
bool b[N];
 
struct A{
	int v,w;
}f[N];
bool operator >(A i,A j) {
	return i.w>j.w||i.w==j.w&&i.v>j.v;
}
vector<A>E[N];

namespace LCA{
int sgn,dep[N],f[N][20],lg[N],g[N][20];	
void dfs(int fa,int u) {
	dfn[u]=++sgn; sz[u]=1;
	dep[u]=!fa?0:dep[fa]+1,f[u][0]=fa;
	for(int i=1;i<=lg[dep[u]];i++) {
		f[u][i]=f[f[u][i-1]][i-1];
	}
	for(int v:V[u]) {
		if(v!=fa) {
			dfs(u,v);
			sz[u]+=sz[v];
		}
	}
}
void dgs(int fa,int u) {
	g[u][0]=sz[fa]-sz[u];
	for(int i=1;i<=lg[dep[u]];i++) {
		g[u][i]=g[u][i-1]+g[f[u][i-1]][i-1];
	}
	for(int v:V[u]) {
		if(v!=fa) dgs(u,v);
	}
}

inline int asksz(int u,int v) {
	for(;f[u][0]!=v;u=f[u][lg[dep[u]-dep[v]-1]]);
//	printf("%d %d\n",u,v);
	return sz[u];
}

inline int sumsz(int u,int v) {
	int ret=0;
	for(;v;u=f[u][lg[v&-v]],v-=v&-v) {
		ret+=g[u][lg[v&-v]];
	}
	return ret;
}
inline int lca(int u,int v) {
	if(dep[u]>dep[v]) swap(u,v);
	for(;dep[u]<dep[v];v=f[v][lg[dep[v]-dep[u]]]);
	if(u==v) return u;
	for(int i=lg[dep[u]];i>=0;i--) {
		if(f[u][i]!=f[v][i]) {
			u=f[u][i],v=f[v][i];
		} 
	}
	return f[u][0];
}
inline int len(int u,int v) {
	return dep[v]-dep[u];
}
inline void init() {
	lg[0]=-1;
	for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
	dfs(0,1);
	dgs(0,1);
}
}

bool cmp(int i,int j) {
	return dfn[i]<dfn[j];
}
void clear(int u) {
	for(A v:E[u]) {
		clear(v.v);
	}
	E[u].clear();
}
void dfs(int u) {
	if(b[u]) f[u]=(A){u,0};
		else f[u]=(A){0,INF};
	for(A v:E[u]){
		dfs(v.v);
		if(f[u]>(A){f[v.v].v,f[v.v].w+v.w}) {
			f[u]=(A){f[v.v].v,f[v.v].w+v.w};
		}
	}
}
void dgs(int u) {
	ans[f[u].v]+=SZ[u];
	int ret=0;
	for(A v:E[u]) {
		if(f[v.v]>(A){f[u].v,f[u].w+v.w}) {
			f[v.v]=(A){f[u].v,f[u].w+v.w};
		}
		if(f[v.v].v==f[u].v) {
			ans[f[u].v]+=LCA::sumsz(v.v,v.w-1);
		} else {
			int y=0;
			if(f[u].v<f[v.v].v) {
				if((v.w+f[u].w-f[v.v].w-1)%2==0) {
					y=(v.w+f[u].w-f[v.v].w-1)>>1;
				} else {
					y=(v.w+f[u].w-f[v.v].w-2)>>1;
				}
			//	x+y=v.w-1
			//	f[u].w+x-f[v.v].w-y=1
			//	y-x=f[u].w-f[v.v].w-1
			} else {
				if((v.w+f[u].w-f[v.v].w-1)%2==0) {
					y=(v.w+f[u].w-f[v.v].w-1)>>1;
				} else {
					y=(v.w+f[u].w-f[v.v].w)>>1;
			//	x+y=v.w-1
			//	f[u].w+x-f[v.v].w-y=-1
			//	y-x=f[u].w-f[v.v].w+1
				}
			}
			y=LCA::sumsz(v.v,y);
			ans[f[v.v].v]+=y; ans[f[u].v]+=LCA::asksz(v.v,u)-y-sz[v.v];
		}
		dgs(v.v);
	}
}

int main(){
	n=rd();
	for(int i=1;i<n;i++) {
		int u=rd(),v=rd();
		V[u].push_back(v),V[v].push_back(u); 
	}
	LCA::init();
	int T=rd();
	while(T--) {
		m=rd(); 
		for(int i=1;i<=m;i++) a[i]=rd(),b[a[i]]=1,fid[i]=a[i];
		sort(a+1,a+m+1,cmp);
		top=1,st[1]=a[1]; SZ[a[1]]=sz[a[1]];
		for(int i=2;i<=m;i++) {
			int l=LCA::lca(a[i],st[top]);
				for(;top>1&&dfn[l]<=dfn[st[top-1]];top--) {
					E[st[top-1]].push_back((A){st[top],LCA::len(st[top-1],st[top])});
					SZ[st[top-1]]-=LCA::asksz(st[top],st[top-1]);
				}
				if(dfn[l]<dfn[st[top]]) {
					SZ[l]=sz[l];
					E[l].push_back((A){st[top],LCA::len(l,st[top])});
					SZ[l]-=LCA::asksz(st[top],l); 
					top--;
				}
				if(!top||st[top]!=l) st[++top]=l;
				st[++top]=a[i]; SZ[a[i]]=sz[a[i]];
		}
		for(;top>1;top--) {
			E[st[top-1]].push_back((A){st[top],LCA::len(st[top-1],st[top])});
			SZ[st[top-1]]-=LCA::asksz(st[top],st[top-1]);
		}
		dfs(st[1]),dgs(st[1]);
		ans[f[st[1]].v]+=n-sz[st[1]];
		for(int i=1;i<=m;i++) {
			printf("%d%c",ans[fid[i]],i==m?'\n':' ');
		}
		for(int i=1;i<=m;i++) ans[a[i]]=0,b[a[i]]=0;
		clear(st[1]);
	}
	return 0;
}

例题2

Luogu P4103 [HEOI2014]大工程

建虚树

第一问：考虑虚树上的每条边\((fa,u)\)，经过边的数量为\((n-sz[u])*sz[u]\)

第二问，第三问：类似求树的直径，处理出最小值，次小值，最大值，次大值

#include<bits/stdc++.h>
#define pb push_back
#define ll long long
const int INF=1e9;
using namespace std;

inline int rd() {
	int ret=0; char ch=getchar();
	while(ch<'0'||ch>'9') {
		ch=getchar();
	}	
	while(ch>='0'&&ch<='9') {
		ret=(ret<<1)+(ret<<3)+ch-'0';
		ch=getchar();
	}
	return ret;
}

const int N=1e6+5;
struct A{ 
	int cnt,he[N],nxt[N<<1],to[N<<1],w[N<<1];
	inline void add(int u,int v,int k) {
		to[++cnt]=v,nxt[cnt]=he[u],he[u]=cnt;
		w[cnt]=k;
	}
}E1,E2;

int lg[N],d[N],dfn[N],sgn,f[N][20],s[N];
void dfs(int fa,int u) {
	dfn[u]=++sgn,d[u]=!fa?0:d[fa]+1,f[u][0]=fa;
	for(int i=1;i<=lg[d[u]];i++) {
		f[u][i]=f[f[u][i-1]][i-1];
	}
	for(int e=E1.he[u];e;e=E1.nxt[e]) {
		int v=E1.to[e];
		if(v!=fa) s[v]=s[u]+1,dfs(u,v);
	}
}
inline int lca(int u,int v) {
	if(d[u]>d[v]) swap(u,v);
	while(d[u]<d[v]) v=f[v][lg[d[v]-d[u]]];
	if(u==v) return u;
	for(int i=lg[d[u]];i>=0;i--) {
		if(f[u][i]!=f[v][i]) {
			u=f[u][i],v=f[v][i];
		}
	}	
	return f[u][0];
}

bool cmp(int i,int j) {
	return dfn[i]<dfn[j];
}

int n,m,st[N],top,siz[N],g1[N],g2[N],h1[N],h2[N]; 
vector<int>V;
bool fl[N];

void clean(int u) {
	fl[u]=siz[u]=g1[u]=g2[u]=h1[u]=h2[u]=0;
	for(int e=E2.he[u];e;e=E2.nxt[e]) {
		int v=E2.to[e]; clean(v);
	}
	E2.he[u]=0;
}

ll ans1; int ans2,ans3;
void dgs(int u) {
	if(fl[u]) siz[u]=1;
	g1[u]=g2[u]=INF,h1[u]=h2[u]=-INF;
	if(fl[u]) g1[u]=0,h1[u]=0;
	for(int e=E2.he[u];e;e=E2.nxt[e]) {
		int v=E2.to[e]; dgs(v);
		siz[u]+=siz[v];
		ans1+=(ll)siz[v]*(m-siz[v])*E2.w[e];
		if(g1[u]>g1[v]+E2.w[e]) {
			g2[u]=g1[u],g1[u]=g1[v]+E2.w[e];
		} else g2[u]=min(g2[u],g1[v]+E2.w[e]);
		if(h1[u]<h1[v]+E2.w[e]) {
			h2[u]=h1[u],h1[u]=h1[v]+E2.w[e];
		} else h2[u]=max(h2[u],h1[v]+E2.w[e]);
	}
	ans2=min(ans2,g1[u]+g2[u]);
	ans3=max(ans3,h1[u]+h2[u]);
}

int main() {
	n=rd();
	for(int i=1;i<n;i++) {
		int u=rd(),v=rd();
		E1.add(u,v,1),E1.add(v,u,1);
	}
	lg[0]=-1;
	for(int i=1;i<=n;i++) {
		lg[i]=lg[i>>1]+1;
	}
	dfs(0,1);
	int q=rd();
	while(q--) {
		m=rd();
		for(int i=1;i<=m;i++) {
			int t=rd(); V.pb(t);
			fl[t]=1;
		}
		if(fl[1]==0) V.pb(1),++m;
		sort(V.begin(),V.end(),cmp);
		st[top=1]=V[0];
		for(int i=1;i<m;i++) {
			int u=lca(st[top],V[i]);
			if(u==st[top]) st[++top]=V[i];
				else {
					while(dfn[st[top-1]]>=dfn[u]) {
						E2.add(st[top-1],st[top],s[st[top]]-s[st[top-1]]);
						top--;
					}
					if(st[top]!=u) {
						E2.add(u,st[top],s[st[top]]-s[u]);
						st[top]=u;
					}
					st[++top]=V[i];
				}
		}
		while(top>1) {
			E2.add(st[top-1],st[top],s[st[top]]-s[st[top-1]]);
			top--;
		}
		if(fl[1]==0) m--;
		ans2=INF; dgs(1);
		printf("%lld %d %d\n",ans1,ans2,ans3);
		V.clear(),E2.cnt=ans1=ans2=ans3=0;
		clean(1);
	}
	return 0;
}

例题3

CF613D Kingdom and its Cities

考虑树形DP（贪心）

对于\(u\),显然每棵子树中至多只有一个点没被封杀（否则联通）；

如果将其在子树内封杀，需要1的代价，但如果在\(u\)点封杀，同样需要1的代价但很明显更加优秀，\(u\)的父亲同理

虚树上DP即可

#include<bits/stdc++.h>
const int INF=1e8;
using namespace std;

const int N=1e5+5;
int n,m,sgn,dfn[N],dad[N],lg[N],f[N],a[N],top,st[N];
bool g[N],b[N];
vector<int>V[N],E[N];
 
namespace LCA{
int dep[N],f[N][20];	
void dfs(int fa,int u) {
	dfn[u]=++sgn; dad[u]=fa;
	dep[u]=!fa?0:dep[fa]+1,f[u][0]=fa;
	for(int i=1;i<=lg[dep[u]];i++) {
		f[u][i]=f[f[u][i-1]][i-1];
	}
	for(int v:V[u]) {
		if(v!=fa) {
			dfs(u,v);
		}
	}

}
inline int lca(int u,int v) {
	if(dep[u]>dep[v]) swap(u,v);
	while(dep[u]<dep[v]) v=f[v][lg[dep[v]-dep[u]]];
	if(u==v) return u;
	for(int i=lg[dep[u]];i>=0;i--) {
		if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
	}
	return f[u][0];
}
}

bool cmp(int i,int j) {
	return dfn[i]<dfn[j];
}
void dgs(int u) {
	f[u]=0,g[u]=0;
	if(b[u]) g[u]=1;
	int sum=0;
	for(int v:E[u]) {
		dgs(v);
		if(b[u]) {
			f[u]+=g[v]+f[v];
		} else {
			sum+=g[v];
			f[u]+=f[v];
		}
	}
	if(!b[u]) {
		if(sum>1) f[u]++;
			else if(sum==1) g[u]=1;
	}
}
void clear(int u) {
	for(int v:E[u]) {
		clear(v);
	}
	E[u].clear();
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<n;i++) {
		int u,v; scanf("%d%d",&u,&v);
		V[u].push_back(v),V[v].push_back(u); 
	}
	lg[0]=-1;
	for(int i=1;i<=n;i++) lg[i]=lg[i>>1]+1;
	LCA::dfs(0,1);
	int T; scanf("%d",&T);
	while(T--) {
		scanf("%d",&m);
		for(int i=1;i<=m;i++) {
			scanf("%d",&a[i]);
			b[a[i]]=1;
		}
		bool fl=0;
		for(int i=1;i<=m;i++) {
			if(b[dad[a[i]]]) {
				for(int j=1;j<=m;j++) b[a[j]]=0;
				puts("-1"); fl=1;
				break;
			}
		}
		if(fl) continue;
		sort(a+1,a+m+1,cmp);
		top=1,st[1]=a[1];
		for(int i=2;i<=m;i++) {
		 		{
				while(top>1&&dfn[l]<=dfn[st[top-1]]) {
					E[st[top-1]].push_back(st[top]);
					top--;
				}
				if(dfn[l]<dfn[st[top]]) {
					E[l].push_back(st[top]);
					top--;
				}
				if(!top||st[top]!=l) st[++top]=l;
				st[++top]=a[i];
		}
		for(;top>1;top--) {
			E[st[top-1]].push_back(st[top]);
		}
		dgs(st[1]);
		printf("%d\n",f[st[1]]); 
		for(int i=1;i<=m;i++) b[a[i]]=0;
		clear(st[1]);
	}
	return 0;
}

例题4

Luogu P4426 [HNOI/AHOI2018]毒瘤

求独立集数目被说的如此花里胡哨

\[f[u][0]=\prod (f[v][0]+f[v][1])\\f[u][1]=\prod f[v][0] \]

显然需要枚举\(m-n+1\)条边的状态，然后树形DP

考虑如何枚举，每条边\((u,v)\) 只有两种限制情况

\(u\)被占据，\(v\)不被占
\(u\)不被占，\(v\)随意

考虑如何提速，根据动态DP的思想，将虚树建出来，由于不存在交叉的路径，未知量之间只有加法(乘法是根本不可能做的)，可以通过预处理系数加速

即：

\[f[u][0]=\prod (w.A0\times f[v][0]+w.B0\times f[v][1])\\ f[u][1]=\prod (w.A1\times f[v][0]+w.B1\times f[v][1]) \]

为方便操作，可以把根节点放到虚树中，就不用考虑第五类点了

第二类点，可以将预处理DP的结果放入节点中

第四类点，可以在预处理路径结果时将预处理DP的结果乘入

第三类点，列式子带入求解

\[f[y][0]=(f[x][0]+f[x][1])\prod C=(\prod C(w.A0+w.A1))f[v][0]+(\prod C(w.B0+w.B1))f[v][1] \\f[y][1]=f[x][0]\prod C=(w.A0\prod C)f[v][0]+(w.B0\prod C)f[v][1] \]

#include<bits/stdc++.h>
#define ll long long 
#define pb push_back
const int p=998244353;
using namespace std;

const int N=1e5+20;
int n,m,cnt,a[N],dfn[N],f[N][2],op[N],top,st[N];
bool b[N];
vector<int>V[N],E[N];
struct A{int u,v; };
vector<A>Q;
struct B{int A0,B0,A1,B1; }W[N];
inline int mo(int x) {
	return x>=p?x-p:x;
}
namespace BCJ {
	int f[N];
	int find(int x) {
		return x==f[x]?x:f[x]=find(f[x]);
	}
	void init() {
		for(int i=1;i<=n;i++) f[i]=i;
	}
}
namespace LCA {
	int sgn,dep[N],lg[N],f[N][20];
	void dfs(int fa,int u) {
		dfn[u]=++sgn; f[u][0]=fa;
		dep[u]=!fa?0:dep[fa]+1;
		for(int i=1;i<=lg[dep[u]];i++) {
			f[u][i]=f[f[u][i-1]][i-1]; 
		} 
		for(int v:V[u]) {
			if(v!=fa) {
				dfs(u,v);
			}
		}
	}
	inline int lca(int u,int v) {
		if(dep[u]>dep[v]) swap(u,v);
		while(dep[u]<dep[v]) v=f[v][lg[dep[v]-dep[u]]];
		if(u==v) return u;
		for(int i=lg[dep[u]];i>=0;i--) {
			if(f[u][i]!=f[v][i]) {
				u=f[u][i],v=f[v][i];
			}
		}
		return f[u][0];
	}
	void init() {
		lg[0]=-1;
		for(int i=1;i<=n;i++) {
			lg[i]=lg[i>>1]+1;
		}
		dfs(0,1);
	}
}
inline bool cmp(int i,int j) {
	return dfn[i]<dfn[j];
}

void dfs(int u) {
	if(!b[u]) {
		f[u][0]=f[u][1]=1;
	}
	for(int v:V[u]) {
		if(v!=LCA::f[u][0]) {
			dfs(v);
			f[u][0]=(ll)f[u][0]*(f[v][0]+f[v][1])%p;
			f[u][1]=(ll)f[u][1]*f[v][0]%p;
		}
	}
}

struct C{int u,v; }g[N];
void dgs(int u) {
	g[u]=(C){1,1};
	for(int v:V[u]) {
		if(f[v][0]||f[v][1]) {
			g[u].u=(ll)g[u].u*(f[v][0]+f[v][1])%p;
			g[u].v=(ll)g[u].v*f[v][0]%p;
		}
    }
	for(int v:E[u]) {
		dgs(v);
		B ret=(B){1,1,1,0},t;
		for(int vv=LCA::f[v][0];vv!=u;vv=LCA::f[vv][0]) {
			for(int k:V[vv]) {
				if(f[k][0]||f[k][1]) {
					ret.A0=(ll)ret.A0*(f[k][0]+f[k][1])%p;
					ret.B0=(ll)ret.B0*(f[k][0]+f[k][1])%p;
					ret.A1=(ll)ret.A1*f[k][0]%p;
					ret.B1=(ll)ret.B1*f[k][0]%p; 
				}	
			}
			t=ret;
			ret.A0=mo(t.A0+t.A1),ret.B0=mo(t.B0+t.B1);
			ret.A1=t.A0,ret.B1=t.B0;
		}
		W[v]=ret;
	}
}
C dhs(int u) {
	C ret=g[u],tmp;
	for(int v:E[u]) {
		tmp=dhs(v);
		ret.u=((ll)tmp.u*W[v].A0+(ll)tmp.v*W[v].B0)%p*ret.u%p;
		ret.v=((ll)tmp.u*W[v].A1+(ll)tmp.v*W[v].B1)%p*ret.v%p;
	}
	if(op[u]==-1) ret.v=0;
		else if(op[u]==1) ret.u=0;
	return ret;
}
int main(){
	scanf("%d%d",&n,&m);
	BCJ::init();
	for(int i=1;i<=m;i++) {
		int u,v; scanf("%d%d",&u,&v);
		int t1=BCJ::find(u),t2=BCJ::find(v);
		if(t1!=t2) {
			V[u].pb(v),V[v].pb(u);
			BCJ::f[t1]=BCJ::f[t2];
		} else {
			Q.pb((A){u,v});
			if(!b[u]) {
				a[++cnt]=u,b[u]=1;
			}
			if(!b[v]) {
				a[++cnt]=v,b[v]=1;
			}
		}
	}
	LCA::init();
	sort(a+1,a+cnt+1,cmp);
	if(a[1]!=1) st[++top]=1;
	if(a[1]) st[++top]=a[1];
	for(int i=2;i<=cnt;i++) {
		int l=LCA::lca(a[i],st[top]); b[l]=1;
		for(;top>1&&dfn[st[top-1]]>=dfn[l];top--) {
			E[st[top-1]].pb(st[top]);
		}
		if(dfn[st[top]]>dfn[l]) {
 			E[l].pb(st[top]);
 			top--;
		}
		if(l!=st[top]) st[++top]=l;
		st[++top]=a[i];
	}
	for(;top>1;top--) {
		E[st[top-1]].pb(st[top]);
	}
	dfs(1);
	dgs(1);
	int ans=0;
	for(int i=0;i<(1<<m-n+1);i++) {
		bool fl=0;
		for(int j=0;j<m-n+1;j++) {
			int u=Q[j].u,v=Q[j].v;
			if((1<<j)&i) {
				if(op[u]==-1||op[v]==1) {
					fl=1; break;
				}
				op[u]=1,op[v]=-1;	
			} else {
				if(op[u]==1) {
					fl=1; break;
				}
				op[u]=-1;
			}
		}
		if(fl) {
			for(int i=1;i<=cnt;i++) op[a[i]]=0;
			continue;
		}
		C ret=dhs(1);
		ans=((ll)ans+ret.u+ret.v)%p;
		for(int i=1;i<=cnt;i++) op[a[i]]=0;
	}
	printf("%d\n",ans);
	return 0;
}

posted @ 2021-03-25 10:12 wwwsfff 阅读(57) 评论(0) 收藏举报

刷新页面返回顶部

wwwsfff

追求主角光环的wsf

虚树

分析

秘诀

例题1

例题2

例题3

例题4

公告