网络流之最大流最小割

简介

没什么好介绍的，作为一个只靠背代码会的dinic，本蒟蒻没什么发言权（毕竟建图才是精华（脸红））
最小割比最大流有趣(恶心)多了
通常网络流的题目数据范围别出心裁，在[50,10000]间，除了DFS想不出别的方法
其中，构造的时候不能出现负边

Dinic模板

Luogu P3376 【模板】网络最大流
有向边需要马上连反边，边权为0
无向边不需要连边权为0的反边

inline int id(int x,int y) {
	return (x-1)*m+y;
}
inline void add(int u,int v,int k) {
	to[++cnt]=v,nxt[cnt]=he[u],he[u]=cnt;
	w[cnt]=k;
}

inline bool bfs() {
	memset(d,0,sizeof(d));
	q[l=r=1]=S; d[S]=1;
	while(l<=r) {
		int u=q[l++];
		for(int e=he[u];e;e=nxt[e]) {
			int v=to[e];
			if(!d[v]&&w[e]) {
				d[v]=d[u]+1; q[++r]=v;
			}
		}
	}
	return d[T]!=0;
}
inline adde(int u,int v,int k) {
        add(u,v,k),add(v,u,0);
}
ll dfs(int u,ll s) {
	if(u==T||s==0) return s;
	ll ret=0;
	for(int e=he[u];e;e=nxt[e]) {
		int v=to[e];
		if(w[e]&&d[v]==d[u]+1) {
			ll t=dfs(v,min(s,w[e]));
			if(!t) d[v]=0;
				else{
					w[e]-=t,w[e^1]+=t;
					s-=t,ret+=t;
				}
		}
	}
	return ret;
}

最大流=最小割

证明：

流\(\leq\)割:显然，对于每一种割，割后的图流为0，即使将割去的边加上，也撑死等于
构造流=割:当流为最大流时，残余网络中不存在\(s\)->\(t\)的通路，将\(s\)能到达的集合设为\(S\)，将剩下的点集设为\(T\),将\(S\)与\(T\)之间的边割掉，显然为一个割，而\(S\)与\(T\)之间的边的权值和显然是最大流（不存在先后关系）

最小割方案构造：

可有边
对残余网络（包括回溯边）求出\(SCC\)，对于满流边\((u,v)\)，如果\(SCC[u]\)!=\(SCC[v]\)，说明此边可在最小割上
可有边一定满足满流且\(SCC[u]\)!=\(SCC[v]\)
证明：缩点后变成DAG的新图的最小割仍然为原图的最小割，所以可为最小割
如果\(SCC[u]\)=\(SCC[v]\)，则可以通过绕一圈减少流量，使其不满流
必须边
对于满流边\((u,v)\)，如果\(SCC[u]\)=\(SCC[S]\),\(SCC[v]\)=\(SCC[T]\) ，说明此边必须在最小割上
必在最小割的边，在残余网络中两端必须和\(S\),\(T\)相连且满流
证明：若满流但在残余网络(此时不包括回溯边)中\(S\)不能到\(u\)或\(v\)不能到T，
那么在每条单独路径上一定都存在一条阻断边，割掉这些阻断边和断掉该边是等价的。其中阻断边一定是可有边
唯一性判定
只存在必须边，不存在可有边，也就是满流边都满足\(SCC[u]\)=\(SCC[S]\),\(SCC[v]\)=\(SCC[T]\)
也就是不存在点，在残余网络中（不包括回溯边）既不与\(S\)连通，也不与连通到\(T\)

例题1

唯一切边

inline void bgs() {
	memset(vis,0,sizeof(vis));
	int l=1,r=1;
	q[1]=T; vis[T]=1;
	while(l<=r) {
		int u=q[l++];
		for(int e=he[u];e;e=nxt[e]) {
			int v=to[e];
			if(!vis[v]&&w[e^1]) {
				vis[v]=1; q[++r]=v;
			}
		}
	}
}
int main(){
scanf("%d%d%d%d",&n,&m,&S,&T);
while(n||m||S||T) {
	cnt=1;
	for(int i=1;i<=n;i++) he[i]=0;
	for(int i=1;i<=m;i++) {
		int u,v,k; scanf("%d%d%d",&u,&v,&k);
		add(u,v,k),add(v,u,k);
	}
	while(bfs()) dfs(S,INF);
	bgs(); bool fl=0;
	for(int i=1;i<=n;i++) {
		if(!vis[i]&&!d[i]) {
			puts("AMBIGUOUS");
			fl=1;
			break;
		}
	}
	if(!fl) puts("UNIQUE");
scanf("%d%d%d%d",&n,&m,&S,&T);
}
	return 0;
}

最大流构图

例题1

卖猪问题
猪笼无限制，故可以用连边表示猪的流动
可以直接从一个人连向下一个有相同猪笼的一个人，连边为INF
\(S\)连向首个打开猪笼的人，连边为猪笼中猪的数量，每个人连向\(T\),边权为需要的猪

int main(){
	scanf("%d%d",&m,&n); S=n+1,T=n+2;
	cnt=1;
	for(int i=1;i<=m;i++) {
		scanf("%d",&a[i]);
	}
	for(int i=1;i<=n;i++) {
		int num; scanf("%d",&num);
		for(int j=1;j<=num;j++) {
			int t; scanf("%d",&t);
			f[i][t]=1;
		}
		int t; scanf("%d",&t);
		add(i,T,t),add(T,i,0);
	}
	for(int k=1;k<=m;k++) {
		bool fl=0;
		for(int i=1;i<=n;i++) {
			if(f[i][k]) {
				if(!fl) {
					add(S,i,a[k]),add(i,S,0);
					fl=1;
				}
				for(int j=i+1;j<=n;j++) {
					if(f[j][k]) {
						add(i,j,INF),add(j,i,0);
						break;
					}
				}
			}
		}
	}
	int ans=0; 
	while(bfs()) {
		ans+=dfs(S,INF);
	}
	printf("%d\n",ans);
	return 0;
}

例题2

Luogu P2891 [USACO07OPEN]Dining G
先考虑只有一种吃的，很简单，略
每头牛只能吃一次，所以裂点，裂成食物点和饮料点，连边权为1的边
每种吃的只能吃一次，所以和原点连边，边权为1，再将吃的和食物点连边，边权为1
喝的同理

int main(){
	scanf("%d%d%d",&n,&m,&K); S=n+n+m+K+1,T=S+1;
	cnt=1;
	for(int i=1;i<=n;i++) {
		int t1,t2; scanf("%d%d",&t1,&t2);
		for(int j=1;j<=t1;j++) {
			int t; scanf("%d",&t);
			add(n+n+t,i,1),add(i,n+n+t,0);
		}
		for(int j=1;j<=t2;j++) {
			int t; scanf("%d",&t);
			add(i+n,n+n+m+t,1),add(n+n+m+t,i+n,0);
		}
	}
	for(int i=1;i<=n;i++) {
		add(i,n+i,1),add(i+n,i,0);
	}
	for(int i=1;i<=m;i++) {
		add(S,n+n+i,1),add(n+n+i,S,0);
	}
	for(int i=1;i<=K;i++) {
		add(n+n+m+i,T,1),add(T,n+n+m+i,0);
	}
	int ans=0; 
	while(bfs()) {
		ans+=dfs(S,INF);
	}
	printf("%d\n",ans);
	return 0;
}

例题3

Luogu P5038 [SCOI2012]奇怪的游戏
黑白点染色，每次一个黑点，一个白点同时加1
设黑点个数为\(a\),白点个数为\(b\),黑点权值和为\(A\),白点权值和\(B\),答案为\(Ans\)
则\(Ans\times a-A\)=\(Ans\times b-B\)
\(\therefore Ans\times (b-a)\)=\(B-A\)

如果\(a\)!=\(b\),则\(Ans\)=\(\frac{B-A}{b-a}\),需要check一下
否则\(A\)=\(B\),因为黑点和白点一样，可以无重叠地覆盖一层，图存在二分性，二分答案，继续check一下

考虑如何check
\(S\)连向所有黑点，边权为\(Ans-\)点权，
黑点和白点连边，边权为INF
白点和\(T\)连边，边权同样为\(Ans-\)点权
判断是否满流

bool check(ll x) {
	cnt=1; S=n*m+1,T=S+1;
	for(int i=1;i<=T;i++) he[i]=0;
	 ll ret=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			if(i+j&1) {
				add(S,id(i,j),x-c[i][j]);
				add(id(i,j),S,0);
				ret+=x-c[i][j]; 
				if(i>1) {
					add(id(i,j),id(i-1,j),INF);
					add(id(i-1,j),id(i,j),0);
				} 
				if(j>1) {
					add(id(i,j),id(i,j-1),INF);
					add(id(i,j-1),id(i,j),0);
				}
				if(i<n) {
					add(id(i,j),id(i+1,j),INF);
					add(id(i+1,j),id(i,j),0);
				}
				if(j<m) {
					add(id(i,j),id(i,j+1),INF);
					add(id(i,j+1),id(i,j),0);
				}
			} else {
				add(id(i,j),T,x-c[i][j]);
				add(T,id(i,j),0);
				ret+=x-c[i][j];
			}
		}
	}
	while(bfs()) {
		ret-=dfs(S,INF)<<1;
	}
	return ret==0;
}

int main(){
int T; scanf("%d",&T);
while(T--) {
	scanf("%d%d",&n,&m); 
	ll A=0,B=0,a=0,b=0,l=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			scanf("%d",&c[i][j]); 
			l=max(l,(ll)c[i][j]);
			if(i+j&1) {
				A+=c[i][j],a++;
			} else {
				B+=c[i][j],b++;
			}
		}
	}
	if(a!=b) {
		if(a>b) swap(A,B),swap(a,b); 
		if((B-A)%(b-a)) {
			puts("-1"); continue;
		} 
		ll t=(B-A)/(b-a);
		if(t>=l&&check(t)) {
			printf("%lld\n",t*(a+b)-A-B>>1); continue;
		}
		puts("-1"); continue;
	} 
	if(A!=B) {
		puts("-1"); continue;
	}
	ll r=1e15,ans=-1,mid;
	while(l<=r) {
		mid=l+r>>1;
		if(check(mid)) ans=mid,r=mid-1;
			else l=mid+1;
	}
	if(ans==-1) puts("-1");
		else printf("%lld\n",ans*(a+b)-A-B>>1);
}
	return 0;
}

例题4

Luogu P3163 [CQOI2014]危桥
由于无向边，所以一次\(S->T,T->S\)可以看作\(S->T\)两遍
将\(S\)连向\(a1\),\(b1\),边权分别为\(an\),\(bn\);\(a2,b2\)连向\(T\)，边权也分别为\(an\),\(bn\)，跑一遍最大流
为了防止\(a1->b2\),\(a2->b1\)这种事情发生，需要将\(S\)连向\(a1,b2\),\(a2,b1\)连向\(T\)，再跑一遍，看是否满流
来自Luogu题解的证明以及分析

int main(){
	while(scanf("%d%d%d%d%d%d%d",&n,&a1,&a2,&an,&b1,&b2,&bn)!=EOF) {
		a1++,a2++,b1++,b2++;  S=n+1,T=n+2;
		for(int i=1;i<=n+2;i++) {
			he[i]=0;
		}
		cnt=1;
		for(int i=1;i<=n;i++) {
			scanf("%s",s[i]+1);
			for(int j=i+1;j<=n;j++) {
				if(s[i][j]=='O') {
					add(i,j,2),add(j,i,2);
				} else if(s[i][j]=='N') {
					add(i,j,INF),add(j,i,INF);
				}
			}
		}	
		add(S,a1,an<<1),add(a1,S,0),add(a2,T,an<<1),add(T,a2,0);
		add(S,b1,bn<<1),add(b1,S,0),add(b2,T,bn<<1),add(T,b2,0);
		int ans=0;
		while(bfs()) {
			ans+=dfs(S,INF);
		}
		if(ans==an+bn<<1) {
			for(int i=1;i<=n+2;i++) {
				he[i]=0;
			}
			cnt=1;
			for(int i=1;i<=n;i++) {
				for(int j=1+i;j<=n;j++) {
					if(s[i][j]=='O') {
						add(i,j,2),add(j,i,2);
					} else if(s[i][j]=='N') {
						add(i,j,INF),add(j,i,INF);
					}
				}
			}
			add(S,a1,an<<1),add(a1,S,0),add(a2,T,an<<1),add(T,a2,0);
			add(S,b2,bn<<1),add(b2,S,0),add(b1,T,bn<<1),add(T,b1,0); 
			ans=0;
			while(bfs()) {
				ans+=dfs(S,INF);
			}
			if(ans==an+bn<<1) {
				puts("Yes");
				continue;
			}
		}
		puts("No");
	}
	return 0;
}

最小割构图之二选一之额外代价

若干件物品，每件物品必须选择\(A\)或者\(B\)，都有对应的权值，其中第\(x\)件和第\(y\)件会产生神奇的化学反应——额外权值

例题1

任务分配
如果两者不相同，增加\(v\)的费用，费用最小，故最小割

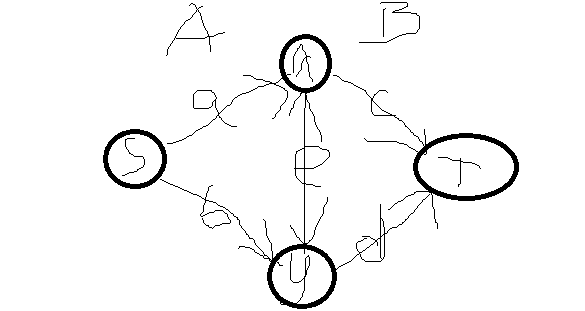
连\(A\)处的边表示\(x\)选择\(A\)
我们只考虑附加权值（点权直接放边上）
两个不同，只能

\[a+e+d=v\\c+e+b=v\\a+b=0\\c+d=0 \]

观察发现：令\(e=v,a=b=c=d=0\)即可，注意加上原来的点权

int main(){
	scanf("%d%d",&n,&m); S=n+1,T=S+1;
	cnt=1;
	for(int i=1;i<=n;i++) {
		int a,b; scanf("%d%d",&a,&b);
		adde(S,i,b),adde(i,T,a);
	}
	for(int i=1;i<=m;i++) {
		int u,v,k; scanf("%d%d%d",&u,&v,&k);
		add(u,v,k),add(v,u,k);
	}
	ll ans=0;
	while(bfs()) {
		ans+=dfs(S,INF);
	}
	printf("%lld\n",ans);
	return 0;
}

例题2（概念上）

关押犯人
理论上无解（可能是我菜）
图同上，只是此时要满足:

\[ c+d=w_1\\a+b=w_2\\b+c+e=w_3\\a+d+e=w_4 \]

发现:

\[e=\frac{w_3+w_4-w_1-w_2}{2} \]

\(e\)为小数没关系，可以同乘2，但\(e\)为负数就是不可以的了，因为最小割必须割掉这条边
所以需要修改

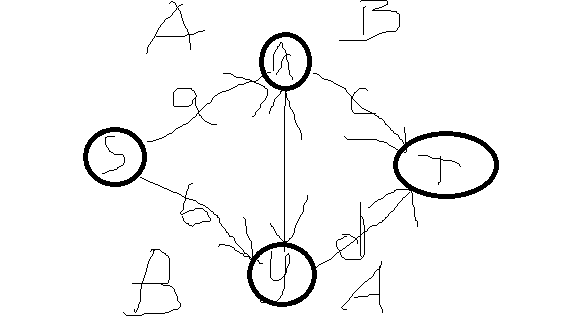
此时：

\[c+b+e=w_1\\a+d+e=w_2\\a+b=w_3\\c+d=w_4 \]

发现：

\[e=\frac{w_1+w_2-w_3-w_4}{2} \]

完美解决了上面的问题
但这存在一个限制条件：新类型的边必须能黑白染色，必须是二分图，所以这是理论上的答案

例题3

幸福值
求最大，所以考虑容斥，变成全部-最小
只考虑附加价值

\[a+b=v1\\c+d=v2\\a+d+e=v1+v2\\c+b+e=v1+v2 \]

发现

\[e=\frac{v1+v2}{2},a=\frac{v1}{2},b=\frac{v1}{2},c=\frac{v2}{2},d=\frac{v2}{2} \]

所有边同乘2，答案也乘2，最后输出是除以2

int main(){
	scanf("%d%d",&n,&m); S=n*m+1,T=S+1;
	cnt=1; int ans=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int t; scanf("%d",&t); ans+=t<<1;
			ss[id(i,j)]+=t<<1;
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int t; scanf("%d",&t); ans+=t<<1;
			tt[id(i,j)]+=t<<1;
		}
	}
	for(int i=1;i<n;i++) {
		for(int j=1;j<=m;j++) {
			scanf("%d",&a[i][j]),ans+=a[i][j]<<1;
		}
	}
	for(int i=1;i<n;i++) {
		for(int j=1;j<=m;j++) {
			scanf("%d",&b[i][j]),ans+=b[i][j]<<1;
		}
	}
	for(int i=1;i<n;i++) {
		for(int j=1;j<=m;j++) {
			add(id(i,j),id(i+1,j),a[i][j]+b[i][j]);
			add(id(i+1,j),id(i,j),a[i][j]+b[i][j]);
			ss[id(i,j)]+=a[i][j];
			ss[id(i+1,j)]+=a[i][j];
			tt[id(i,j)]+=b[i][j];
			tt[id(i+1,j)]+=b[i][j];
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<m;j++) {
			scanf("%d",&a[i][j]),ans+=a[i][j]<<1;
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<m;j++) {
			scanf("%d",&b[i][j]),ans+=b[i][j]<<1;
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<m;j++) {
			add(id(i,j),id(i,j+1),a[i][j]+b[i][j]);
			add(id(i,j+1),id(i,j),a[i][j]+b[i][j]);
			ss[id(i,j)]+=a[i][j];
			ss[id(i,j+1)]+=a[i][j];
			tt[id(i,j)]+=b[i][j];
			tt[id(i,j+1)]+=b[i][j];
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			adde(S,id(i,j),ss[id(i,j)]);
			adde(id(i,j),T,tt[id(i,j)]);
		}
	}
	while(bfs()) {
		ans-=dfs(S,INF);
	}
	printf("%d\n",ans>>1);
	return 0;
}

例题4

炮塔攻击

将其攻击看作覆盖，发现每个位子最多会被覆盖两次，横着一遍，竖着一遍，要求至多被覆盖一次

所以联想到最小割（裂点，与\(S\)连边的点表示横着的，与\(T\)连边的点表示竖着）

横点和竖点连边为INF（无法割掉）

求最大值，经典容斥，变成全部-最小割

这里的全部含义不同了，指的每门炮最大的收益

以炮往上轰为例，某个点往上方相邻的点连边的边权设为最大收益-该点收益，这条边没了表示选轰离\(S\)较近的点

int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};

int main(){
	scanf("%d%d",&n,&m); S=n*m*2+1,T=S+1;
	cnt=1;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			scanf("%d",&a[i][j]); 
		}	
	}
	int ans=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			if(a[i][j]<0) {
				int fx=-a[i][j]-1;
				int ii=i,jj=j,mx=0;
				while(0<ii+dx[fx]&&ii+dx[fx]<=n&&0<jj+dy[fx]&&jj+dy[fx]<=m) {
					ii+=dx[fx],jj+=dy[fx];
					mx=max(mx,a[ii][jj]); 
				}
				ans+=mx;
				if(fx<=1) {
					vis1[j]=1;
					adde(S,id(i,j),INF);
					ii=i,jj=j;
					while(0<ii+dx[fx]&&ii+dx[fx]<=n&&0<jj+dy[fx]&&jj+dy[fx]<=m) {
						adde(id(ii,jj),id(ii+dx[fx],jj+dy[fx]),mx-max(a[ii][jj],0));
						ii+=dx[fx],jj+=dy[fx];
					}
				} else {
					vis2[i]=1;
					adde(id(i,j)+n*m,T,INF);
					ii=i,jj=j;
					while(0<ii+dx[fx]&&ii+dx[fx]<=n&&0<jj+dy[fx]&&jj+dy[fx]<=m) {
						adde(id(ii+dx[fx],jj+dy[fx])+n*m,id(ii,jj)+n*m,mx-max(a[ii][jj],0));
						ii+=dx[fx],jj+=dy[fx];
					}
				}
			}
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			if(vis1[j]&&vis2[i]) adde(id(i,j),id(i,j)+n*m,INF);
		}
	}
	while(bfs()) ans-=dfs(S,INF);
	printf("%d\n",ans); 
	return 0;
}

例题5

Luogu P3973 [TJOI2015]线性代数

看见线代别慌，直接写代数含义

\[\begin{split} D&=(A\times B-C)\times A^T \\&=\sum_{i=1}^{n}a_{i}\times\sum_{j=1}^{n}(b[j][i]\times a_j-c[j]) \\&=\sum_{i=j}^{n}\sum_{j=1}^{n}a_ia_jb[j][i]-\sum_{i=1}^{n}a_ic[j] \end{split} \]

观察到\(a\)只有01，可以与\(S\)连边表示选0，与\(T\)连边表示选1

法1：最大权闭合图选边一定能到达点，理论上TLE

法2：全部正值-最小割，点权b[i][i],c[i],直接加上，考虑附加价值

\[a+b=0\\c+d=b[i][j]+b[j][i]\\a+e+d=b[i][j]+b[j][i]\\c+b+e=b[i][j]+b[j][i] \]

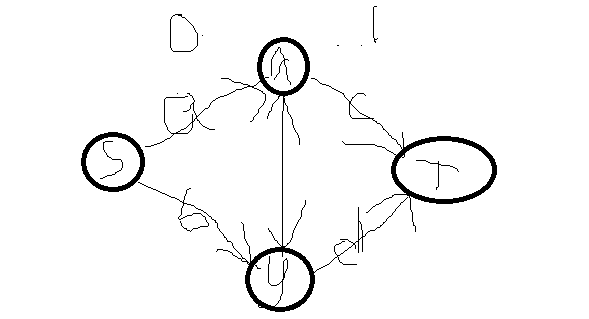
则

\[c=d=e=\frac{b[i][j]+b[j][i]}{2}\\a=b=0 \]

都乘以2

int main(){
	scanf("%d",&n); S=n+1,T=S+1;
	cnt=1; ll ans=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=n;j++) {
			scanf("%d",&b[i][j]); 
			ans+=b[i][j]<<1;
		}	
	}
	for(int i=1;i<=n;i++) {
		int t; scanf("%d",&t);
		adde(i,T,t<<1); 
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=n;j++) {
			if(i!=j) adde(i,j,b[i][j]+b[j][i]);
		}
	}
	for(int i=1;i<=n;i++) {
		int sum=0;
		for(int j=1;j<=n;j++) {
			sum+=b[i][j]+b[j][i];
		}
		adde(S,i,sum);
	}
	while(bfs()) ans-=dfs(S,INF);
	printf("%lld\n",ans>>1); 
	return 0;
}

最小割构图之最大权闭合图

选择该种方式通常劣于前者，但思维难度低
选\(A\)必须选\(A\)能到达的所有点
从\(S\)连向所有点权为正的点，连边为点权
从所有点权为负的点连向\(T\),连边为-点权
图中的边连起来，点权为INF
答案为正点权和-最小割

例题1

Luogu P4313 文理分科
求最大值，即为所有值-最小割
令额外费用为额外点，而选额外点，必须选构成额外条件的点，所以为最大权闭合图
但不能像上面一样连边，\(S\)连出表示选文科，连到\(T\)表示选理科

int main(){
	scanf("%d%d",&n,&m); S=n*m*3+1,T=S+1;
	cnt=1;int ans=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int t; scanf("%d",&t);
			adde(id(i,j),T,t); ans+=t;
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int t; scanf("%d",&t);
			adde(S,id(i,j),t); ans+=t;
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int t; scanf("%d",&t);
			int now=id(i,j)+n*m;
			adde(now,T,t),ans+=t;
			adde(id(i,j),now,INF);
			if(i>1) adde(id(i-1,j),now,INF);
			if(j>1) adde(id(i,j-1),now,INF);
			if(i<n) adde(id(i+1,j),now,INF);
			if(j<m) adde(id(i,j+1),now,INF); 
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int t; scanf("%d",&t);
			int now=id(i,j)+n*m*2;
			adde(S,now,t),ans+=t;
			adde(now,id(i,j),INF);
			if(i>1) adde(now,id(i-1,j),INF);
			if(j>1) adde(now,id(i,j-1),INF);
			if(i<n) adde(now,id(i+1,j),INF);
			if(j<m) adde(now,id(i,j+1),INF); 
		}
	}
	while(bfs()) ans-=dfs(S,INF);
	printf("%d\n",ans); 
	return 0;
}

例题2

Luogu P2805 [NOI2009] 植物大战僵尸
必须按拓扑序删，选\(i\)必须删\(i\)之前的点，所以又是最大闭合图
但由于其中会有环，环上以及环后的节点无敌，所以拓扑排序DFS，标记能到达的所有节点加入图中

int main(){
	scanf("%d%d",&n,&m); S=n*m+1,T=S+1;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			scanf("%d",&c[i][j]);
			int num; scanf("%d",&num);
			for(int k=1;k<=num;k++) {
				int u,v; scanf("%d%d",&u,&v);
				u++,v++;
				V[id(i,j)].push_back(id(u,v)); 
				deg[id(u,v)]++;
			}
			if(j<m) {
				V[id(i,j+1)].push_back(id(i,j));
				deg[id(i,j)]++;
			}
		}	
	}
	int l=1,r=0;
	for(int i=1;i<=n*m;i++) {
		if(!deg[i]) q[++r]=i;
 	}
	while(l<=r) {
		int u=q[l++];
		for(auto v:V[u]) {
			deg[v]--;
			if(!deg[v]) q[++r]=v;
		}
	}
	cnt=1; int ans=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			if(!deg[id(i,j)]) {
				if(c[i][j]>0) {
					adde(S,id(i,j),c[i][j]);
					ans+=c[i][j];
				} else {
					adde(id(i,j),T,-c[i][j]);
				}
				for(auto v:V[id(i,j)]){
					if(!deg[v]) {
						adde(v,id(i,j),INF);
					}
				}
			}
		}
	}
	while(bfs()) ans-=dfs(S,INF);
	printf("%d\n",ans); 
	return 0;
}

最小割之最小密度图构图

选若干点，求最小的密度

例题1

矛盾指数
分数规划，所以二分答案\(\eta\)

\[\eta\leq \frac{y}{x}\Leftrightarrow \eta x-y\leq 0 \]

法1：

\[\eta x-y\leq 0\Leftrightarrow0\leq y-\eta x \]

所以求\(y-\eta x\) 的最大值

有观察到对于每条边，选了边以后必须选点，所以最大权闭合图

bool check(db mid) {
    cnt = 1;
    db ret = 0;
    for (int i = 1; i <= T; i++) he[i] = 0;
    for (int i = 1; i <= m; i++) {
        adde(S, i, 1);
        ret++;
        int u = E1[i], v = E2[i];
        adde(i, u + m, INF), adde(i, v + m, INF);
    }
    for (int i = 1; i <= n; i++) {
        adde(i + m, T, mid);
    }
    while (bfs()) {
        ret -= dfs(S, INF);
    }
    return ret >= eps;
}

int main() {
    scanf("%d%d", &n, &m);
    S = n + m + 1, T = S + 1;
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &E1[i], &E2[i]);
    }
    db l = 0, r = 200, mid, ans = 0;
    while (l <= r) {
        mid = (l + r) / 2;
        if (check(mid)) {
            ans = mid;
            l = mid + eps;
        } else
            r = mid - eps;
    }
    check(ans);
    int num = 0;
    for (int i = 1; i <= n; i++) {
        if (d[i + m]) {
            num++;
        }
    }
    printf("%d\n", num);
    for (int i = 1; i <= n; i++) {
        if (d[i + m]) {
            printf("%d\n", i);
        }
    }
    return 0;
}

法2：

将上式求\(\eta x-y\)的最小值写成\(\sum\)的形式,其中选出的人是\(V\)

\[=\eta\sum_{v\in V}1-\sum_{(u,v)\in E,u,v\in V}1 \]

对后一个\(\sum\)以进行容斥

\[=\sum_{v\in V}\eta-\frac{\sum_{(u,v)\in E,v\in V}1-\sum_{(u,v)\in C[V,G-V]}1}{2}\\=\sum_{v\in V}(\eta-\frac{deg[v]}{2})+\frac{\sum_{(u,v)\in C[V,G-V]}1}{2} \]

将所有值同乘2(对判断正负无影响)

\[=\sum_{v\in V}(2\eta-deg[v])+\sum_{(u,v)\in C[V,G-V]}1 \]

可以发现后一个\(\sum\)是割，且一定是最小割（考虑选完节点后，最小分开点集的边一定是两两连边和）

所以连边，连向\(T\)的边表示选该点，\(S\)流出的边表示不选，边权和点权一样，

考虑到点权可以为负数，故同时加上\(m\)，其他边正常连

bool check(db mid) {
    cnt = 1;
    for (int i = 1; i <= T; i++) he[i] = 0;
    for (int i = 1; i <= m; i++) {
        int u = E1[i], v = E2[i];
        add(u, v, 1), add(v, u, 1);
    }
    for (int i = 1; i <= n; i++) {
        adde(i, T, (db)m - deg[i] + 2 * mid);
        adde(S, i, (db)m);
    }
    db ret = n * m;
    while (bfs()) {
        ret -= dfs(S, INF);
    }
    return ret >= eps;
}

int main() {
    scanf("%d%d", &n, &m);
    S = n + 1, T = S + 1;
    for (int i = 1; i <= m; i++) {
        scanf("%d%d", &E1[i], &E2[i]);
        deg[E1[i]]++, deg[E2[i]]++;
    }
    db l = 0, r = 200, mid, ans = 0;
    while (l <= r) {
        mid = (l + r) / 2;
        if (check(mid)) {
            ans = mid;
            l = mid + eps;
        } else
            r = mid - eps;
    }
    check(ans);
    int num = 0;
    for (int i = 1; i <= n; i++) {
        if (d[i]) {
            num++;
        }
    }
    printf("%d\n", num);
    for (int i = 1; i <= n; i++) {
        if (d[i]) {
            printf("%d\n", i);
        }
    }
    return 0;
}

posted @ 2021-03-11 13:20 wwwsfff 阅读(185) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

wwwsfff

追求主角光环的wsf