DirectX RayTracing (4) RayTracingInOneWeekend
DirectX RayTracing (4) RayTracingInOneWeekend
目前为止 DXR 的基本功能都已经讲述完毕,这次我要使用先前讲述的功能复刻 RayTracing In One Weekend 的部分章节,主要是光追框架的搭建、材质的实现以及重要性采样的实现,重要性采样的部分目前还有点问题,最后收敛的结果有点不正确,后续再找找问题出在哪里。
光追的原理已经在第一篇文章中简要描述过了,这里就不赘述了,在先前的框架中,每个像素都只会发射一根光线,也就是1 SPP,光线击中物体后也没有考虑物体的表面属性,只沿着反射方向跟踪光线,最后渲染的结果是有偏的。而在实际的物理模型中,光线会在物体的表面发生吸收、反射和折射,在介质中还会发生散射,因此当光线击中物体后,不能只是简单的沿着反射方向追踪光线,而是要根据表面的微观结构(即材质),沿着光线可能发散的方向追踪光线,这个过程其实就是在整个球面上求解渲染方程。但是在计算机中无法处理连续积分,因此通常使用随机数及概率论来进行近似,通常会使用蒙特卡洛积分来将连续的积分离散化,然后根据光线的概率分布发射光线。
蒙特卡洛积分
渲染方程描述了光线与物体表面的相互作用,它是一个在半球面上的积分:
在计算机中,我们无法求解这个连续积分。蒙特卡洛积分提供了一种离散的近似方法:随机采样,及通过随机选取**样本点并进行采样计算的方式来通过有限的离散计算近似积分。上述公式的积分部分可以重写为以下形式 :
可以看到近似的结果与概率论中的期望值求法十分类似,实际上蒙特卡洛积分的核心思想就来自期望值,上述公式实际上是再求函数 \(g(x) = \frac{f(x)}{p(x)}\) 的期望值,其中 \(p(x)\) 为任意一种分布的概率分布函数(PDF)。当 N 越大,及采样数越大,离散求和的形式与积分结果越接近,当 N 趋于无穷的时候,两端严格相等。
上述公式的推到过程如下,为了求解一个复杂的积分 \(I = \int_a^b f(x) dx\) ,我们可以将其重写为以下形式 \(I = \int_a^b \frac{f(x)}{p(x)} \cdot p(x) dx\) ,而某一函数的期望值的积分形式为 \(E[f(X)] = \int_a^bf(x) \cdot p(x)dx\) ,通过比较可以发现积分 \(I\) 可以通过计算函数 \(\frac{f(x)}{p(x)}\) 的期望求得,及 \(I = E[\frac{f(X)}{p(x)}]\) 。这里需要注意的是所选择的概率分布函数需要是归一化的,及在积分域中积分的值为 1。
随机数生成
上面提到求解渲染方程可以通过将积分转换为离散求和的形式进行求解,这就要面临采样点选择的问题,所选择的采样点需要符合 PDF 的分布,直接生成符合分布的随机数一般较为麻烦。因此通常使用两种方法来生成某种分布的随机数,一种方法是拒绝法,及生成一个均匀分布的随机数,若该数在分布函数的范围内,则接受该数成为采样点;若是不在范围内,则拒绝该数,重新生成随机数直到符合 PDF 为止。一个比较形象的例子是若是想要生成一个位于单位圆内的随机点,则在 [-1, 1] 内随机生成两个随机数作为采样点,若该采样点到圆心的距离小于半径,则接受该采样点,否则重新生成。第二种方法为反演法,该方法可以将一个均匀分布的随机变量转换为服从任意目标分布的随机变量,该过程使用的转化函数为目标分布的累计分布函数(CDF)的逆函数,CDF 表示给定随机变量 X,其取值小于 x 的概率, CDF 的定义如下:
其中 \(p(x)\) 为先前提到过的概率分布函数 PDF。因此反演法的步骤可分为以下三步:
- 计算目标概率分布函数 \(p(x)\) 的累计分布函数 \(P(x)\)。
- 计算 CDF 的逆函数。
- 生成一个均匀分布的随机变量并使用 \(P^{-1}(x)\) 将其变换到目标分布。
上面讲述的两种任意分布的随机数的生成方法都需要使用均匀分布的随机数,因此在实现光追之前还需要在 HLSL 内实现随机数的生成。常用的 GPU 内随机数生成有两种,一种是在 CPU 端生成随机数并保存到 Texture 中,在 GPU 中通过对纹理进行采样来获得随机数;第二种是直接在 HLSL 中实现随机数算法。前者省去了随机数生成的开销,但是需要占用大量的显存,同时纹理采样也有一定的开销;后者则是所有计算都需要在 GPU 中进行,若随机数生成开销过大,效率会不够理想。这里我是用了第二种方法,直接在 GPU 中计算随机数,我对随机数的生成没有过多了解,因此我直接使用了 AI 帮我实现的置换同余生成器。生成随机数的过程如下:
struct PCGState
{
uint state;
};
uint Hash(uint x)
{
x = (x ^ 61u) ^ (x >> 16);
x *= 9u;
x ^= (x >> 4);
x *= 0x27d4eb2du;
x ^= (x >> 15);
return x | 1u;
}
// 初始化PCG状态
PCGState PCG_Init(uint2 pixel, uint frameIndex)
{
PCGState rng;
rng.state = Hash(pixel.x * 1973u ^ pixel.y * 9277u ^ frameIndex * 26699u);
// warm up
[unroll]
for (int i = 0; i < 3; ++i) {
rng.state = rng.state * 747796405u + 2891336453u;
}
return rng;
}
// 生成32位随机整数(会更新 state)
uint RandomUint(inout PCGState rng)
{
rng.state = rng.state * 747796405u + 2891336453u;
uint word = ((rng.state >> ((rng.state >> 28u) + 4u)) ^ rng.state) * 277803737u;
return (word >> 22u) ^ word;
}
注意这里每次生成随机数需要传入随机数状态,而且必须要使用inout关键字,这个关键字类似 C++ 中的引用,对该值的修改会保存下来。这里的随机数状态后续需要保存在光追负载中,不能作为全局的静态变量,因为在不同 Shader ,例如 Ray Generation Shader 和 Closest Hit Shader 的全局静态变量并不共享,若是作为静态变量则同一像素内的不同 Shader 所对应的随机数状态是相同的,会造成统一像素内的生成的随机数是不均匀的,导致收敛错误。这里还实现了基于上述随机数的常用函数,具体实现如下:
uint RandomUint(inout PCGState rng, uint min, uint max)
{
if (min >= max)
return min;
uint range = max - min + 1u;
return min + (RandomUint(rng) % range);
}
float RandomFloat(inout PCGState rng)
{
return float(RandomUint(rng)) * (1.0 / 4294967296.0);
}
float RandomFloat(inout PCGState rng, float min, float max)
{
return lerp(min, max, RandomFloat(rng));
}
int RandomInt(inout PCGState rng, int min, int max)
{
if (min >= max)
return min;
uint range = uint(max - min) + 1u;
uint scale = RandomUint(rng) % range;
return min + int(scale);
}
float2 RandomFloat2(inout PCGState rng)
{
return float2(RandomFloat(rng), RandomFloat(rng));
}
float2 RandomFloat2(inout PCGState rng, float2 min, float2 max)
{
return lerp(min, max, RandomFloat2(rng));
}
float3 RandomFloat3(inout PCGState rng)
{
return float3(RandomFloat(rng), RandomFloat(rng), RandomFloat(rng));
}
float3 RandomFloat3(inout PCGState rng, float3 min, float3 max)
{
return lerp(min, max, RandomFloat3(rng));
}
float4 RandomFloat4(inout PCGState rng)
{
return float4(RandomFloat(rng), RandomFloat(rng), RandomFloat(rng), RandomFloat(rng));
}
float4 RandomFloat4(inout PCGState rng, float4 min, float4 max)
{
return lerp(min, max, RandomFloat4(rng));
}
// 生成均匀分布的随机向量(单位球面)
float3 RandomUnitVector(inout PCGState rng)
{
float r1 = RandomFloat(rng);
float r2 = RandomFloat(rng);
float sinPhi = sqrt((1.0 - r2) * r2);
float theta = 2.0 * sPI * r1;
float x = cos(theta) * sinPhi;
float y = sin(theta) * sinPhi;
float z = 1 - 2 * r2;
return float3(x, y, z);
}
// 在半球体上生成均匀随机方向
float3 RandomOnHemiSphere(inout PCGState rng, float3 normal)
{
float3 dir = RandomUnitVector(rng);
dir = dot(dir, normal) < 0 ? -dir : dir;
return dir;
}
// 单位圆盘上的均匀随机点
float2 RandomInUnitDisk(inout PCGState rng)
{
float radius = sqrt(max(0.0, RandomFloat(rng)));
float angle = RandomFloat(rng, 0, 2 * sPI);
return float2(cos(angle), sin(angle)) * radius;
}
// 生成余弦加权的向量
float3 RandomCosineDirection(inout PCGState rng)
{
float r1 = RandomFloat(rng);
// 随机极角
float phi = 2 * sPI * r1;
// 随机半径
float r2 = sqrt(RandomFloat(rng));
float x = cos(phi) * r2;
float y = sin(phi) * r2;
float z = sqrt(1 - r2 * r2);
return float3(x, y, z);
}
其中最后四个函数就是使用了上述两种方法的随机数生成,由于拒绝法生成随机数通常涉及 for 循环,不适合在 GPU 上使用,因此这里都使用了反演法,具体的推到过程可以看 RayTracing In One Weekend 原篇。
光追框架
Ray Generation Shader
本次示例代码沿用之前的框架,后续只会列出主要的区别,根据文章开头的框架更改描述,在 Ray Generation Shader 中需要调用多次 TraceRay,同时在同一个像素内也需要进行随机偏移,因此 Ray Generation Shader 的实现如下:
[shader("raygeneration")]
void RaygenShader()
{
// Generate GenerateCameraRayParams
......
// 初始化随机数状态
PCGState pcgState = PCG_Init(index, asuint(frameIndex * totalTime));
float4 color = float4(0,0,0,1);
uint spp = uint(samplesPerPixel);
for(uint sampleIndex = 0; sampleIndex < spp; ++sampleIndex){
RayTracing::Ray ray = GenerateCameraRay(index, cameraPos, viewportStart, pixelDeltaU, pixelDeltaV, pcgState);
color += TraceRadianceRay(ray, 0, pcgState);
}
color /= spp;
// Write Texture
......
}
每个像素对应的 Ray Generation Shader 都会往场景中发射多根光线,最后计算所有光线的平均值。此步骤对应蒙特卡洛积分的求和步骤。每次生成光线的时候都会对光线的起点进行随机偏移来抗锯齿:
RayTracing::Ray GenerateCameraRay(GenerateCameraRayParams params, inout PCGState rng)
{
// 在像素内随机取样
float2 offset = RandomFloat2(rng);
offset -= 0.5f; // [-0.5, 0.5]
float2 pixelOffset = float2(params.index) + offset; // 进行随机偏移
float3 pixelSample = params.viewportStart + pixelOffset.x * params.pixelDeltaU + pixelOffset.y * params.pixelDeltaV;
float3 center = params.cameraPos
RayTracing::Ray ray;
ray.origin = center;
ray.direction = normalize(pixelSample - ray.origin);
return ray;
}
Closest Hit Shader
调用TraceRay之后,若是光线击中物体,就会调用 Closest Hit Shader,在该 Shader 中我们需要完成对表面材质的模拟,根据材质的特性生成光线并调用TraceRay,具体的实现如下:
struct Surface
{
float3 position;
float3 normal;
bool frontFace;
float2 uv;
float3 color;
};
[shader("closesthit")]
void ClosestHitShader_Triangle(inout RayTracing::RayPayload payload, in BuiltInTriangleIntersectionAttributes attrs)
{
// Get GeometryData
......
if(GetMaterialScatter(lMaterialCB, surface, scatterRecord, payload.rng)){
Ray ray;
ray.origin = surface.position;
ray.direction = normalize(rayDir);
float4 scatterCol = TraceRadianceRay(ray, payload.depth, rng);
payload.color = float4(scatterRecord.attenuation, 1) * scatterCol;
}
else{
payload.color = float4(0,0,0,1);
}
}
在函数GetMaterialScatter中会进行表面材质的计算,前两个参数为传入的材质属性和表面属性,第三个参数为输出的散射信息,包含材质的表面颜色和散射方向,其具体实现如下:
struct ScatterRecord
{
Ray scatterRay;
float3 attenuation;
};
bool GetMaterialScatter(
MaterialConstants materialCB,
Surface surface,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
switch(materialCB.type) {
case RayTracing::MaterialType::Lambertian: {
return ScatterLambertian(surface, materialCB.matDataOffset, scatterRecord, rng);
}
case RayTracing::MaterialType::Metal: {
return ScatterMetal(surface, materialCB.matDataOffset, scatterRecord, rng);
}
case RayTracing::MaterialType::Dielectric: {
return ScatterDielectric(surface, materialCB.matDataOffset, scatterRecord, rng);
}
case RayTracing::MaterialType::DiffuseLight: {
return ScatterDiffuseLight(surface, materialCB.matDataOffset, scatterRecord, rng);
}
default:
return false;
}
return false;
}
根据常量缓冲区中的材质类型,该函数会调用对应材质的计算,具体计算过程后续详细讲述。
除了这些变化外,其他基本与上一篇文章的示例相同,加速结构的构建与先前完全一致,若是不熟悉的可看看上一篇,ShaderTable 的构建只更改了材质常量缓冲区的写入。根签名的部分只为新绑定的资源添加了对应的根参数。Intersection Shader 和 Miss Shader 也与之前相同。
材质的实现
此部分的实现完全与 Ray Tracing In One Weekend 相同,材质函数的输入为物体的几何属性,例如位置、法线、纹理坐标等,还有对应材质的种类及数据;函数的输出为发生吸收后表面的颜色和下一次TraceRay的方向。输入的材质数据会从两个地方获得,一是物体对应的常量缓冲区,才 CPU 端会将一个局部根签名绑定到 Hit Group 中,材质相关的数据会从 Shader Table 中写入,若是对这一块不熟悉可以看上一篇文章,常量缓冲区中保存了材质的类型及对应数据在 Buffer 中的偏移,其定义如下:
namespace MaterialType{
enum Type{
Lambertian = 0,
Metal,
Dielectric,
DiffuseLight,
Count
};
}
struct MaterialConstants
{
MaterialType::Type type;
uint matDataOffset;
};
第二个材质的数据是各个材质需要使用的数据,由于不同材质使用的数据的大小不同,因此不适合使用StructuredBuffer,这里使用了ByteAddressBuffer来进行储存,对应的偏移量保存在上面提到的 CBV 中,为了方便获取各个材质的数据,我增加了一些辅助函数:
namespace MaterialType{
struct LambertianMatData{
float3 albedo;
};
struct MetalMatData{
float3 albedo;
float fuzz;
};
struct DielectricMatData{
float refractiveIndex;
};
struct DiffuseLightMatData{
float3 emitColor;
};
static const uint MaterialDataSize[MaterialType::Count] = {
12, // Lambertian
16, // Metal
4, // Dielectric
12 // Light
};
}
// 材质数据缓冲区
ByteAddressBuffer gMaterialBuffer : register(t0, space1);
RayTracing::MaterialType::LambertianMatData GetLambertianMaterialData(uint matDataOffset)
{
RayTracing::MaterialType::LambertianMatData matData;
uint3 data = gMaterialBuffer.Load3(matDataOffset);
matData.albedo = asfloat(data);
return matData;
}
RayTracing::MaterialType::MetalMatData GetMetalMaterialData(uint matDataOffset)
{
RayTracing::MaterialType::MetalMatData matData;
uint4 data = gMaterialBuffer.Load4(matDataOffset);
matData.albedo = asfloat(data.xyz);
matData.fuzz = asfloat(data.w);
return matData;
}
RayTracing::MaterialType::DielectricMatData GetDielectricMaterialData(uint matDataOffset)
{
RayTracing::MaterialType::DielectricMatData matData;
uint data = gMaterialBuffer.Load(matDataOffset);
matData.refractiveIndex = asfloat(data);
return matData;
}
RayTracing::MaterialType::DiffuseLightMatData GetDiffuseLightMaterialData(uint matDataOffset)
{
RayTracing::MaterialType::DiffuseLightMatData matData;
uint3 data = gMaterialBuffer.Load3(matDataOffset);
matData.emitColor = asfloat(data);
return matData;
}
各个函数做的工作其实就是从 Buffer 中获取数据并返回,不过这里有一点需要注意一下,由于ByteAddressBuffer::Load方法只能返回 uint 类型,所以需要手动将数据转化为原来的类型。注意加载得到的数据的二进制数据都为原来类型的二进制数据,并没有强制转换为 uint 类型,因此不能直接强转位对应的类型,类似(float)data,这会发生类型转换而发生的位转换,导致数据错误,需要使用内置函数asfloat来在不进行位转换的同时转换为 float 类型。
漫反射材质
漫反射材质没有透射,只有反射和吸收,吸收用物体表面的颜色来描述,而反射通常使用 Lambertian 分布来进行描述,及物体表面接收到的 radiance 与入射光线和法线的夹角 θ 的余弦值,及 \(cosθ\) 成正比,因此可以通过在法线半球方向上以 \(cosθ\) 的概率反射光线来实现,在计算机中通常使用随机变量来描述概率分布,因此可以通过如下方式实现:
bool ScatterLambertian(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
RayTracing::MaterialType::LambertianMatData matData = GetLambertianMaterialData(matDataOffset);
float3 scatterDir = surface.normal + RandomUnitVector(surface.seed);
if(NearZero(scatterDir)){
scatterDir = surface.normal;
}
scatterRecord.scatterRay = { surface.position, scatterDir };
attenuation = surface.color * matData.albedo;
return true;
}
金属材质
对于完全抛光过的金属,不会随机反射光线,而是会沿着反射方向反射光线,因此只需要使用入射光线及法线计算出光线的反射方向并调用TraceRay即可,具体的实现如下:
bool ScatterMetal(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
RayTracing::MaterialType::MetalMatData matData = GetMetalMaterialData(matDataOffset);
// 反射光线
float3 reflected = reflect(WorldRayDirection(), surface.normal);
scatterRecord.scatterRay = { surface.position, reflected };
scatterRecord.attenuation = surface.color * matData.albedo;
return true;
}
对于表面粗糙的金属,其反射后会沿着以反射方向为轴的一个圆锥进行前进,因此需要引入一个额外的参数来描述金属的粗糙程度,然后根据粗糙程度对反射光线进行圆锥上的随机偏移,大致过程可用下图进行描述:
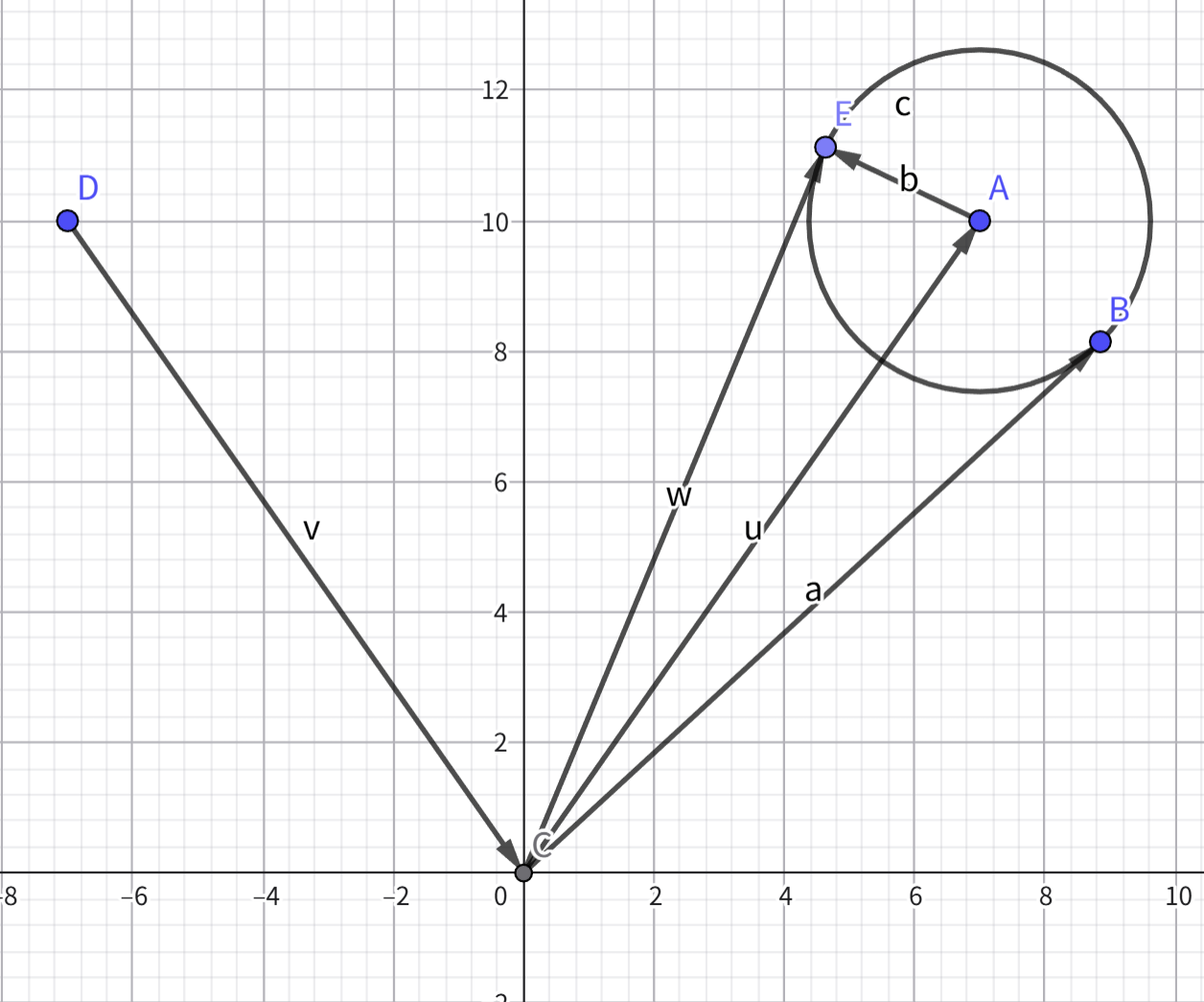
光线 v 经过表面反射后,会生成一根在向量 a 与 w 之间的光线,该光线可通过向量 u 与向量 b 相加得到,而描述粗糙程度的参数会作为向量 b 的长度来控制最后反射光线的偏移量,当粗糙度位 0 是则会只沿着一个方向反射。具体的实现如下:
bool ScatterMetal(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
RayTracing::MaterialType::MetalMatData matData = GetMetalMaterialData(matDataOffset);
// 反射光线
float3 reflected = reflect(WorldRayDirection(), surface.normal);
// 在光锥内进行随机偏移
scatterDir = reflected + matData.fuzz * RandomUnitVector(rng);
scatterRecord.scatterRay = { surface.position, scatterDir }
scatterRecord.attenuation = surface.color * matData.albedo;
return (dot(scatterDir, surface.normal) > 0);
}
由于最后偏移后的向量可能会不在半球方向内,因此进行额外的检测,若是不在半球内则返回 false ,不发射光线。
电介质材质
光线折射
电介质是现实中常遇见的一类材质,玻璃、水等物质都属于电介质,相比前两种材质,电介质材质最大的区别就是其透射率较大,也就是折射现象十分明显。
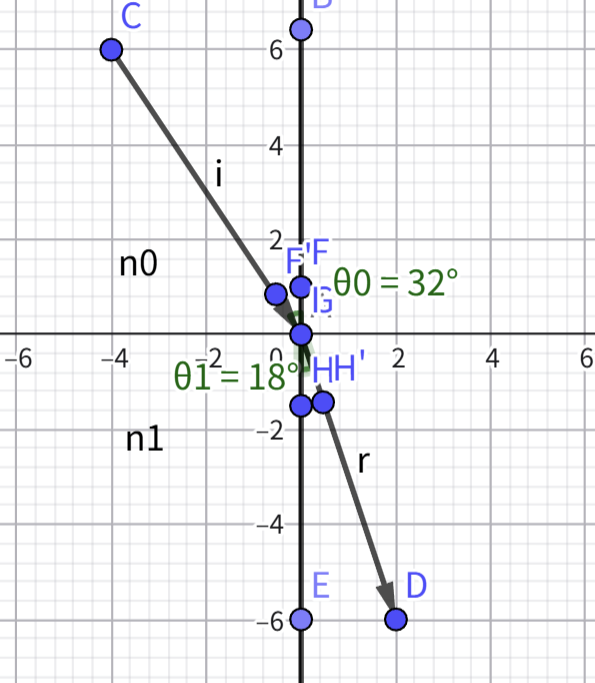
折射通常使用折射率 n 来进行描述,折射率又分为绝对折射率与相对折射率,绝对折射率是当前物质相对与真空的折射率,也就是光线从真空中射向物体会发生的折射强度;而相对折射率描述的是光线从一种介质 0 入射到介质 1 时的折射率,若是用 \(n_0\) 和 \(n_1\) 来分别描述当前介质和另一种介质的绝对折射率,则当前物质的相对折射率为 \(\frac{n_1}{n_0}\) ,这个结论在多层电介质的时候十分有用。
折射现象通常用菲涅尔定律来进行描述,其定义如下:
也可以写成如下形式:
其中 \(θ_0\) 和 \(θ_1\) 分别表示光线在介质 0 和 在介质 1 时与界面法线之间的夹角。根据菲涅尔定律,我们就可以根据入射光线的方向和法线方向计算出折射方向。折射的实现如下:
bool ScatterDielectric(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
RayTracing::MaterialType::DielectricMatData matData = GetDielectricMaterialData(matDataOffset);
scatterRecord.attenuation = surface.color;
// 根据表面方向决定折射率
float refractionRatio = surface.frontFace ? (1.0f / matData.refractiveIndex) : matData.refractiveIndex;
float3 unitDirection = WorldRayDirection();
float cosTheta = min(dot(-unitDirection, surface.normal), 1.0f);
scatterRecord.scatterRay.direction = refract(unitDirection, surface.normal, refractionRatio);
scatterRecord.scatterRay.origin = surface.position;
return true;
}
全反射
当光线从光密介质(折射率较大的一端介质)入射到光疏介质中,且角度满足一定条件(全反射角)时就可以发生全反射现象,该现象具体表现为光线全都反射回光密介质中,没有折射分量。其实光线实际是进入了光疏介质的,并在内部发生了多次反射,最后才回到光密介质中,不过这属于物理光学的内容,暂且不讨论。全反射角可以从菲涅尔定律中推到而出,由于折射光线最大的角度为 90 度,因此将 \(θ_1 = 90\) 带入方程中,可得到:
经过数学变换后可以得到:
其中 \(\frac{n_1}{n_0}\) 就是相对折射率,因此实际计算中只需要计算入射角的 sin 值后和折射率比较即可。通过添加如下代码即可实现全反射:
bool ScatterDielectric(...)
{
scatterRecord.emission = float3(0,0,0);
RayTracing::MaterialType::DielectricMatData matData = GetDielectricMaterialData(matDataOffset);
scatterRecord.attenuation = surface.color;
// 根据表面方向决定折射率
float refractionRatio = surface.frontFace ? (1.0f / matData.refractiveIndex) : matData.refractiveIndex;
float3 unitDirection = WorldRayDirection();
float cosTheta = min(dot(-unitDirection, surface.normal), 1.0f);
float sinTheta = sqrt(1.0f - cosTheta * cosTheta);
// 发生全反射
bool cannotRefract = refractionRatio * sinTheta > 1.0f;
// 根据蒙特卡洛方法决定反射或折射
if(cannotRefract){
scatterRecord.scatterRay.direction = reflect(unitDirection, surface.normal);
} else {
scatterRecord.scatterRay.direction = refract(unitDirection, surface.normal, refractionRatio);
}
scatterRecord.scatterRay.origin = surface.position;
return true;
}
反射率及折射率
真实的物理世界中入射光线部分能量被折射,使用折射率描述,同时部分能量被反射,使用反射率描述,其中两者的和应当为一,两者各自的占比通常使用菲涅尔反射进行描述,而完整的菲涅尔反射过于复杂,因此通常使用 Schlick 近似来进行计算:
float Reflectance(float cosine, float refractionIndex) {
// Use Schlick's approximation for reflectance.
float r0 = (1 - refractionIndex) / (1 + refractionIndex);
r0 = r0 * r0;
return r0 + (1 - r0) * pow((1 - cosine), 5);
}
该函数的返回值为物体的反射率,其中 r0 为反射系数,折射率可通过1 - Reflectance(...)进行计算。具体实现时应该 Trace 两根光线,分别获取反射分量和折射分量,然后乘上对应的反射率或折射率,但这样性能消耗过大,因此使用蒙特卡洛方法进行近似,根据概率分布来判断是需要折射还是反射,随后的实现如下:
bool ScatterDielectric(...)
{
RayTracing::MaterialType::DielectricMatData matData = GetDielectricMaterialData(matDataOffset);
scatterRecord.attenuation = surface.color;
// 根据表面方向决定折射率
float refractionRatio = surface.frontFace ? (1.0f / matData.refractiveIndex) : matData.refractiveIndex;
float3 unitDirection = WorldRayDirection();
float cosTheta = min(dot(-unitDirection, surface.normal), 1.0f);
float sinTheta = sqrt(1.0f - cosTheta * cosTheta);
// 发生全反射
bool cannotRefract = refractionRatio * sinTheta > 1.0f;
// 计算基于菲涅尔反射的反射率
// 反射系数
float r0 = (1.0 - refractionRatio) / (1.0 + refractionRatio); // 近似计算
// 反射率
r0 = r0 * r0;
float condition = r0 + (1.0 - r0) * pow(1.0 - cosTheta, 5.0);
// 根据蒙特卡洛方法决定反射或折射
if(cannotRefract || condition > RandomFloat(rng)){
scatterRecord.scatterRay.direction = reflect(unitDirection, surface.normal);
} else {
scatterRecord.scatterRay.direction = refract(unitDirection, surface.normal, refractionRatio);
}
scatterRecord.scatterRay.origin = surface.position;
return true;
}
实现玩所有的材质后即可实现如下效果:

三个大球就分别用了三种材质。
景深
现实中的相机由多个透镜组组合而成,各个透镜组合之后会有其自身的焦距,通过更改镜头或是进行调焦可以更改其焦距。若物体处在交点处,相机就会清晰成像;否则就会模糊成像。可用下图来辅助理解:

相机的透镜前方的物经过透镜后会在相机处形成对应的像,假设物到透镜的距离为 \(s\) ,在透镜后形成的像到透镜的距离为 \(s_1\) ,透镜的焦距为 f ,则三者满足以下公式,该公式也称为薄透镜成像公式:
当物距离透镜的位置保持一定距离时,物反射或发出的光线经过在相机处清晰成像,此时经过物与透镜平行的平面就是焦平面,若是物在此平面上移动,光线经过透镜后都会在相机处形成一个焦点,从而清晰成像:
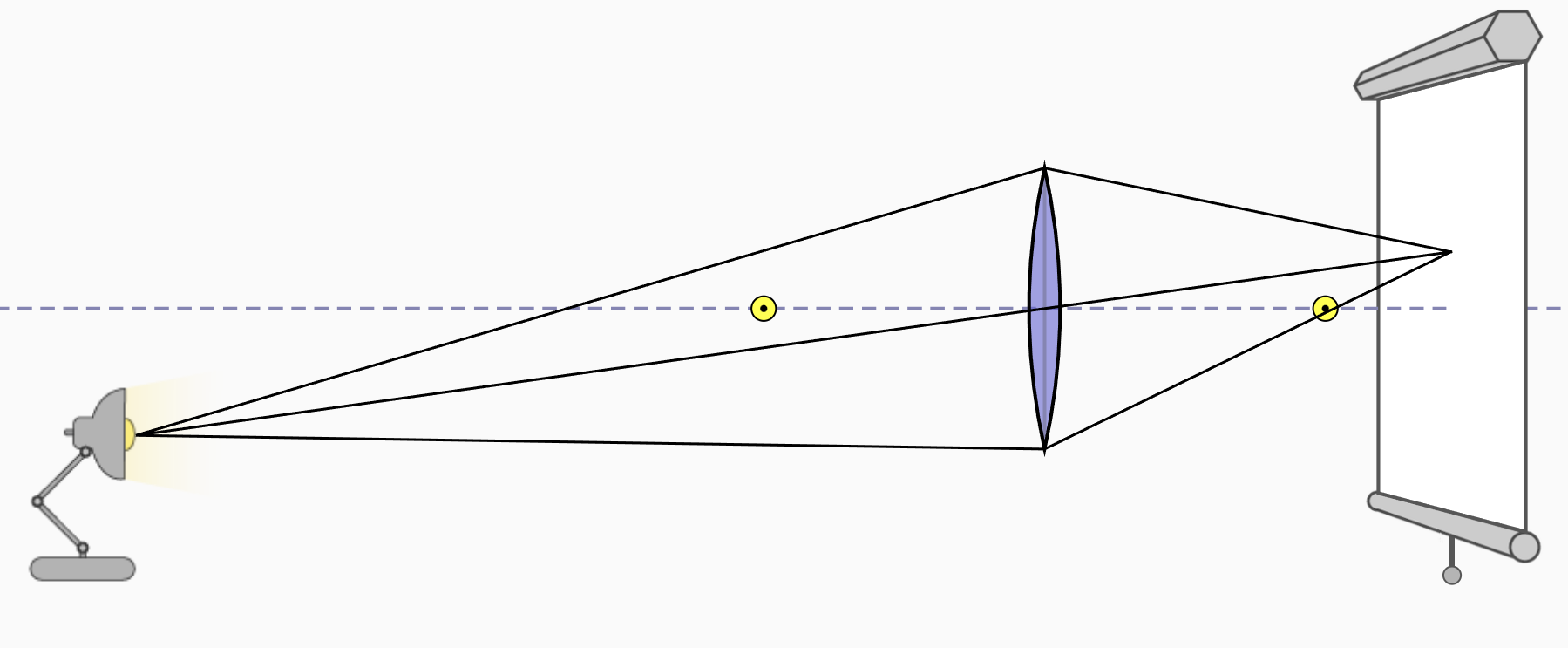
当物远离焦平面时,都无法在相机处形成交点,而是形成一个弥散圆,从而发生失焦,导致画面模糊、背景虚化。

而所谓的景深就是借由该原理形成,当物体在焦平面处,物在相机底片处清晰成像。距离焦面越远,弥散圆越大,在相机底片处形成的画面越模糊。在光栅化管线中,通常使用屏幕后处理的方法进行景深的实现,实现方法有很多种,这里简要举两个实现方案:
- 在后处理阶段中对整个纹理进行模糊处理,通常使用高斯模糊,每个像素使用深度图中的深度计算对应的模糊半径,然后使用该半径进行模糊处理。
- 使用预先设定的较大模糊半径对整个纹理进行模糊处理,来作为完全失焦的图像,每个像素使用深度图中的深度计算模糊权重,使用该权重在原图像与模糊图像之间进行插值。
这两种方法实现起来都较为简单,且性能开销较低,还有很多更复杂、画面更好的景深实现方法,这里就不过多介绍了
而在光追管线中,没有深度图可以使用,因此无法使用屏幕后处理的方法。这里使用的方法与 Ray Tracing In One Weekend 相同,及以相机为中心生成一个散焦圆盘,来模拟弥散圆,同时将视口放在焦面处,随机在散焦圆盘中生成一个采样点作为射线的中心,沿着视口中对应的像素发射光线。
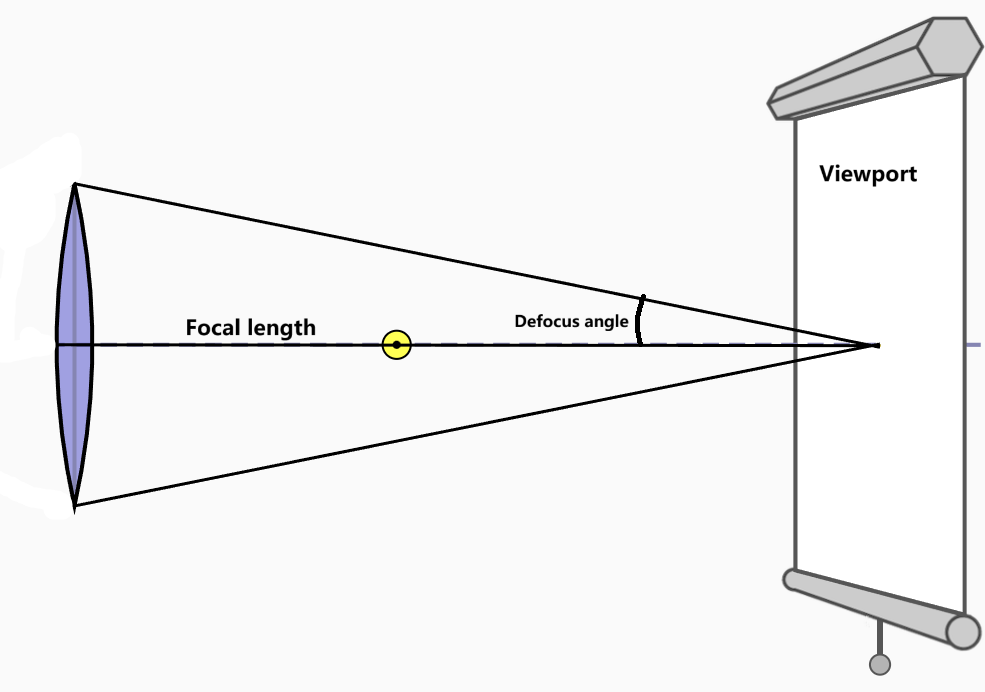
由于视口处在焦面处,因此若是物体处在焦平面处,光线只会采样到焦点处的物体,离焦平面越远,对应的散焦圆盘越大,采样到其他物体的可能性越大,就会形成模糊的效果。通过调节相机的焦距和对应的散焦角度,就可以调节散焦圆盘的大小,也可以调节模糊程度。
具体的实现也较为简单,首先需要将相机的焦距和散焦角度通过常量缓冲区传到 Shader 中,这里更改了全局根签名中对应的常量缓冲区:
// 场景的常量缓冲区
struct SceneConstantBuffer
{
// 生成光线使用的数据
float4 cameraPos;
float4 viewportUAndFrameIndex;
float4 viewportVAndSamplePerPixel;
float4 backgroundColorAndTotalTime;
float2 focusDistAndDefocusAngle; // 焦距和散焦角度
float numImportanceSamplingObjects;
float pad;
};
void RayTracer::TraceRays(ComputeCommandList &cmdList)
{
...
static uint32_t frameIndex = 0;
float focusDist = imgui.focusDist;
auto h = std::tan(m_Camera->GetFovY() * .5f);
auto viewportHeight = 2 * h * focusDist;
float viewportWidth = viewportHeight * (float(width) / height);
RayTracing::SceneConstantBuffer sceneCB{};
sceneCB.cameraPos = Math::Vector4{m_Camera->GetPosition()};
sceneCB.viewportUAndFrameIndex = Math::Vector4{m_Camera->GetRightAxis() * viewportWidth, float(frameIndex++)};
sceneCB.viewportVAndSamplePerPixel = Math::Vector4{-m_Camera->GetUpAxis() * viewportHeight, float(imgui.samplesPerPixel)};
sceneCB.backgroundColorAndTotalTime = Math::Vector4{imgui.backgroundColor, GameCore::g_Timer.TotalTime()};
sceneCB.focusDistAndDefocusAngle = std::pair{focusDist, imgui.defocusAngle * float(std::numbers::pi) / 180.0f};
sceneCB.numImportanceSamplingObjects = static_cast<float>(m_ProceduralGeometryManager->GetAllImportanceSamplingObjects().size());
...
}
随后在 Ray Generation Shader 中计算散焦圆的半径,并使用该半径在圆中随机生成一个采样点作为光线的中心:
RayTracing::Ray GenerateCameraRay(GenerateCameraRayParams params, inout PCGState rng)
{
// 在像素内随机取样
float2 offset = RandomFloat2(rng) + params.subPixelIndex;
offset *= params.invSPP;
offset -= 0.5f;
float2 pixelOffset = float2(params.index) + offset;
float3 pixelSample = params.viewportStart + pixelOffset.x * params.pixelDeltaU + pixelOffset.y * params.pixelDeltaV;
// 进行散焦模糊的随机偏移
float2 defocusDisk = RandomInUnitDisk(rng);
float3 center = params.cameraPos + defocusDisk.x * params.defocusU + defocusDisk.y * params.defocusV;
RayTracing::Ray ray;
ray.origin = center;
ray.direction = normalize(pixelSample - ray.origin);
return ray;
}
[shader("raygeneration")]
void RaygenShader()
{
...
// 计算散焦模糊参数
float defocusRadius = focusDist * tan(defocusAngle * 0.5f);
float3 defocusU = normalize(viewportU) * defocusRadius;
float3 defocusV = normalize(viewportV) * defocusRadius;
GenerateCameraRayParams genParams;
genParams.defocusU = defocusU;
genParams.defocusV = defocusV;
...
}
由此就可以实现景深的效果,我将相机焦距和散焦角度作为参数设置在 Imgui 中进行调节,最后的效果如下:
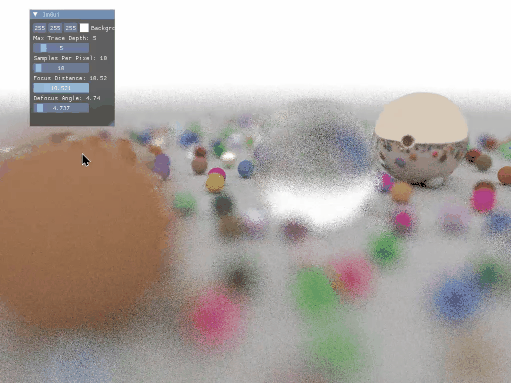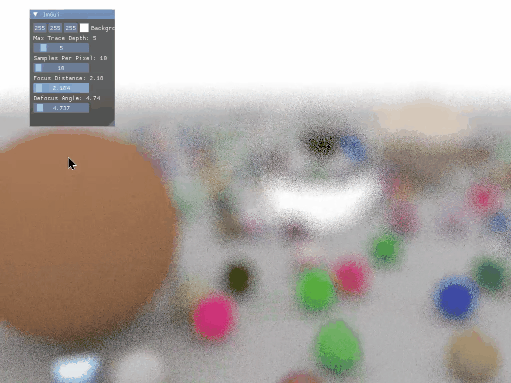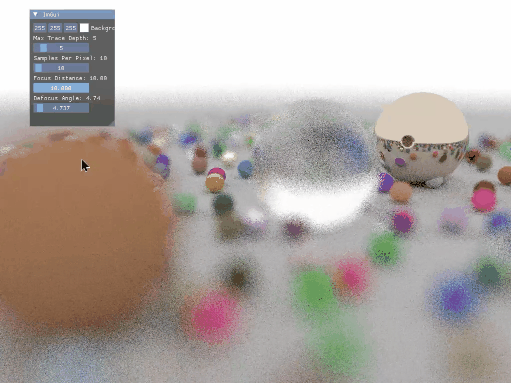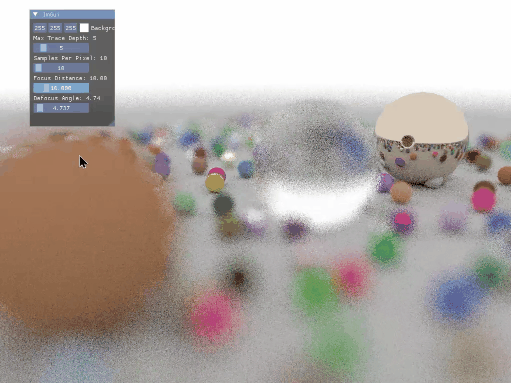
光源的实现
光源的实现也较为简单,当光线击中光源材质的时候,返回光源的颜色并终止 TraceRay 。实现如下:
struct ScatterRecord
{
Ray scatterRay;
float3 attenuation;
float3 emission;
};
float4 GetColor(inout RayTracing::RayPayload payload, Surface surface)
{
Ray incomingRay = {WorldRayOrigin(), WorldRayDirection()};
ScatterRecord scatterRecord;
float4 color = 0;
[branch]
if(!GetMaterialScatter(lMaterialCB, surface, scatterRecord, payload.rng)){
return float4(scatterRecord.emission, 1);
}
color = TraceRadianceRay(scatterRecord.scatterRay, payload.depth, payload.rng);
color *= float4(scatterRecord.attenuation, 1);
color.rgb += scatterRecord.emission;
return color;
}
光源材质的实现如下:
namespace MaterialType{
enum Type{
Lambertian = 0,
Metal,
Dielectric,
DiffuseLight,
Count
};
struct DiffuseLightMatData{
float3 emitColor;
};
static const uint MaterialDataSize[MaterialType::Count] = {
12, // Lambertian
16, // Metal
4, // Dielectric
12 // Light
};
}
RayTracing::MaterialType::DiffuseLightMatData GetDiffuseLightMaterialData(uint matDataOffset)
{
RayTracing::MaterialType::DiffuseLightMatData matData;
uint3 data = gMaterialBuffer.Load3(matDataOffset);
matData.emitColor = asfloat(data);
return matData;
}
bool ScatterDiffuseLight(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
// 发光材质不散射光线
scatterRecord.attenuation = float3(0,0,0);
scatterRecord.scatterRay = (Ray)0;
if(surface.frontFace) { // 单面光源
RayTracing::MaterialType::DiffuseLightMatData matData = GetDiffuseLightMaterialData(matDataOffset);
scatterRecord.emission = matData.emitColor * surface.color;
}
return false; // 不继续 TraceRay
}
分层采样
蒙特卡洛积分虽然可以使用离散求和来近似连续积分,但其近似程度与采样数紧密相关,及近似所产生的噪声(标准差)与采样数的平方成反比,因此采样数提升到原来的四倍,噪声才会减少到原来的一半,这就会导致收敛的速度越来慢,通过使用分层采样可以减缓这种边际效应的递减。在原先的实现中,每个像素都会追踪多根光线,每根光线都会在其对应的像素中进行随机偏移,现在根据采样数将每个像素划分为一个网格,每个采样点平均分配到一个网格中,同时在网格中的子像素内进行随机偏移。


使用分层采样的方法可以避免由于随机数产生的样点聚集现象,从而减少噪声的产生。但是当问题的维度越大,分层采样所带来的收益也就会随之减小,而光追过程中多次反射的特点导致其维度会随着反射数的增加而增加,每反射一次,就会增加两个维度 \(α_0\) 和 \(θ_0\) 用以描述反射方向的立体角。这里暂时只对每个像素生成的光线进行分层处理,反射光线的分层采样暂不处理。
分层采样的实现也较为简单,这需要在 Ray Generation Shader 中稍加修改即可:
RayTracing::Ray GenerateCameraRay(GenerateCameraRayParams params, inout PCGState rng)
{
// 在像素内随机取样
float2 offset = RandomFloat2(rng) + params.subPixelIndex;
offset *= params.invSPP;
offset -= 0.5f;
...
}
[shader("raygeneration")]
void RaygenShader()
{
...
float4 color = float4(0,0,0,1);
uint sqrtSPP = uint(sqrt(samplesPerPixel));
uint spp = sqrtSPP * sqrtSPP;
if(spp == 0) {
gOutput[index] = float4(0, 0, 0, 1);
return;
}
genParams.invSPP = 1.0f / float(spp);
for(uint i = 0; i < sqrtSPP; ++i){
for(uint j = 0; j < sqrtSPP; ++j){
genParams.subPixelIndex = uint2(i, j);
RayTracing::Ray ray = GenerateCameraRay(genParams, pcgState);
float4 sampleColor = TraceRadianceRay(ray, 0, pcgState);
color += sampleColor;
}
}
color /= spp;
...
}
分层采样之前:

分层采样之后:

可以看到物体的边界处相比之前更清晰了,当画面更高频时效果更明显。但老实说其实看着没啥区别。
重要性采样
重要性采样的理论基础就是先前介绍过的蒙特卡洛积分,其主要的思想就是通过收集场景中需要重要性采样的位置,根据收集的位置确定概率分布函数 PDF 并应用到渲染过程中。
表面散射的PDF
在实现重要性采样之前,我们还需要构建渲染过程中需要使用的 PDF。首先是对渲染方程的等价变化,原先的渲染方程形式如下:
我们需要更改为使用概率密度函数进行描述,这里假设所有的 BRDF 都可以用以下形式进行表达:
其中 A 为入射光反射散射的百分比,也就是物体所呈现的颜色,pScatter 表示在单位立体角上光线发生散射的概率,也就是散射的概率密度函数。将该表达式带入渲染方程后可得到如下形式:
使用蒙特卡洛积分可将其表达为求和形式:
N 越大近似结果越接近原函数,当 N -> ∞ 时两者严格相等。当随机生成的 PDF \(p(\omega_o)\) 与散射 PDF 相等时,就可以得到如下表达式:
可以看到这个表达式的形式与我们现在实现的光追渲染相同:
float4 GetColor(inout RayTracing::RayPayload payload, Surface surface)
{
...
color = TraceRadianceRay(scatterRecord.scatterRay, payload.depth, payload.rng);
color *= float4(scatterRecord.attenuation, 1);
color.rgb += scatterRecord.emission;
return color;
}
要实现重要性采样,就不能简单的认为散射 PDF 与 我们选择的 PDF 相同,因此此处就需要修改为如下形式:
struct ScatterRecord
{
Ray scatterRay;
float3 attenuation;
float3 emission;
bool skipPDF;
PDFType pdfType;
};
float4 GetColor(inout RayTracing::RayPayload payload, Surface surface)
{
...
// 根据 pdf 进行采样
[branch]
if(scatterRecord.skipPDF) {
color = TraceRadianceRay(scatterRecord.scatterRay, payload.depth, payload.rng);
color *= float4(scatterRecord.attenuation, 1);
}
else{
float3 pdfSampleDir = SamplePDF(scatterRecord.pdfType, surface, payload.rng);
Ray scatterRay;
scatterRay.origin = surface.position;
scatterRay.direction = pdfSampleDir;
// 获取材质的 PDF
float pdfVal = GetPDFValue(scatterRecord.pdfType, incomingRay, scatterRay, surface);
// 材质在特定方向进行散射的概率
float scatterPDF = GetScatteringPDF(lMaterialCB.type, incomingRay, scatterRay, surface);
color = TraceRadianceRay(scatterRay, payload.depth, payload.rng);
color = (color * float4(scatterRecord.attenuation, 1) * scatterPDF) / pdfVal;
}
color.rgb += scatterRecord.emission;
return color;
}
其中这里有三个函数与 PDF 相关:SamplePDF根据传入的 PDF 类型生成一个随机的采样方向作为下一次TraceRay的方向;GetPDFValue根据传入的 PDF 类型计算采样点处的 PDF 值,也就是 \(p(\omega_o)\);GetScatteringPDF用于计算散射 PDF,也就是 \(pScatter(p, \omega_i, \omega_o, \lambda)\)。由于有些材质有明确的反射分布,例如电介质、金属等,不需要使用蒙特卡洛积分进行近似,直接沿着反射或折射方向TraceRay即可,因此这里引入了一个变量skipPDF来判断是否需要跳过近似计算,该参数会在计算材质的时候进行赋值。
由于电介质和金属都不需要使用 PDF ,因此只需要实现 \(Lambertian\) 材质的 PDF 即可。 \(Lambertian\) 材质的 PDF 与 \(cos(\theta_o)\) 成正比,因此可使用如下表达式 \(pScatter(p, \omega_i, \omega_o, \lambda) = C * cos(\theta_o)\) ,由于 PDF 在定义域内的和为 1,因此**下可表示为:
最后求解出 \(C = \frac{1}{\pi}\) ,因此 \(Lambertian\) 材质的 PDF 可表示为 \(pScatter(p, \omega_i, \omega_o, \lambda) = \frac{cos(\theta_o)}{\pi}\) ,具体实现如下:
float GetScatteringPDF(RayTracing::MaterialType::Type matType, Ray incomingRay, Ray scatterRay, Surface surface)
{
switch(matType){
case RayTracing::MaterialType::Lambertian: {
float3 normal = surface.normal;
float cosTheta = max(dot(normal, normalize(scatterRay.direction)), 0.0f);
return cosTheta / sPI;
}
default:
return 0.0f;
}
}
由于后续要使用混合 PDF,及同时考虑光源的 PDF 与物体表面的 PDF,因此在材质的实现代码中,不仅需要添加是否跳过 PDF,还需要添加 PDF 类型的赋值:
enum PDFType
{
SpherePDF,
CosinePDF,
ImportanceSamplingPDF,
Count
};
bool ScatterLambertian(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
...
scatterRecord.skipPDF = false;
scatterRecord.pdfType = PDFType::CosinePDF;
return true;
}
bool ScatterMetal(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
...
scatterRecord.skipPDF = true;
return (dot(scatterDir, surface.normal) > 0);
}
bool ScatterDielectric(
Surface surface,
uint matDataOffset,
out ScatterRecord scatterRecord,
inout PCGState rng)
{
...
scatterRecord.skipPDF = true;
return true;
}
在 Lambertian 材质中添加的 PDF 为余弦加权的 PDF,具体推导就不推导了,使用的也是反演法,实现如下:
// 生成余弦加权的向量
float3 RandomCosineDirection(inout uint state)
{
float r1 = RandomFloat(state);
// 随机极角
float phi = 2 * sPI * r1;
// 随机半径
float r2 = sqrt(RandomFloat(state));
float x = cos(phi) * r2;
float y = sin(phi) * r2;
float z = sqrt(1 - r2 * r2);
return float3(x, y, z);
}
// 正交基变换
float3 OrthonormalBasisTransform(float3 normal, float3 dir)
{
normal = normalize(normal);
float3 a = abs(normal.x) > 0.9 ? float3(0, 1, 0) : float3(1, 0, 0);
float3 tangent = normalize(cross(normal, a));
float3 bitangent = cross(normal, tangent);
float3x3 TBN = float3x3(bitangent, tangent, normal);
dir = dir[0] * TBN[0] + dir[1] * TBN[1] + dir[2] * TBN[2];
return dir;
}
// 余弦加权半球采样的PDF值
float GetCosinePDF(float3 normal, float3 dir)
{
float cosTheta = max(dot(normal, normalize(dir)), 0.0f);
return cosTheta / sPI;
}
float3 SampleCosinePDF(float3 normal, inout PCGState rng)
{
return OrthonormalBasisTransform(normal, RandomCosineDirection(rng));
}
几何体数据的传输
前面也提到过重要性采样就是将采样光线集中在光线更有可能来的位置,而在光追中所有的光照都来自光源,除了环境光,场景中的所有的光照都源自先前实现实现的光源材质,因此只需要对使用光源材质的几何体进行重要性采样即可,这时问题就转换为了对几何体进行重要性采样,接下来就是要实现光源的 PDF 以及对各种几何体的采样。
在实现光源的 PDF 之前,还需要将重要性采样使用的几何体上传到 GPU,这里使用了StructuredBuffer和ByteAddressBuffer来储存几何信息,StructuredBuffer中储存了几何体的类型和几何数据的偏移量,ByteAddressBuffer中储存了几何体的实际数据,由于重要性采样的几何体可能有多个,因此在全局的常量缓冲区中需要添加一个几何体的数量。
// 场景的常量缓冲区
struct SceneConstantBuffer
{
...
float numImportanceSamplingObjects;
float pad;
};
namespace ImportanceSampling {
enum ImportanceSamplingPrimitiveType
{
Sphere = 0,
Quad,
Count
};
// 重要性采样对象
struct ImportanceSamplingObject
{
ImportanceSamplingPrimitiveType type;
uint primitiveDataOffset;
};
static const uint ImportanceSamplingDataSize[ImportanceSamplingPrimitiveType::Count] = {
16, // Sphere
100 // Quad
};
struct SphereData
{
float3 center;
float radius;
};
struct QuadData
{
float4x4 worldToObj;
float3 q;
float3 u;
float3 v;
};
}
这里还添加了几个辅助获取数据的函数:
StructuredBuffe r<RayTracing::ImportanceSampling::ImportanceSamplingObject> gImportanceSamplingObjects : register(t0, space2);
ByteAddressBuffer gImportanceSamplingObjectDataBuffer : register(t1, space2);
// Importance Sampling Data Getters
RayTracing::ImportanceSampling::SphereData GetSphereData(uint offset)
{
RayTracing::ImportanceSampling::SphereData sphere;
// 获取球心和半径
uint3 data = gImportanceSamplingObjectDataBuffer.Load3(offset);
offset += 12;
sphere.center = asfloat(data);
data.x = gImportanceSamplingObjectDataBuffer.Load(offset);
sphere.radius = asfloat(data.x);
return sphere;
}
RayTracing::ImportanceSampling::QuadData GetQuadData(uint offset)
{
RayTracing::ImportanceSampling::QuadData quad;
// 变换矩阵
for(int i = 0; i < 4; i++)
{
uint4 data = gImportanceSamplingObjectDataBuffer.Load4(offset);
offset += 16;
quad.worldToObj[i] = asfloat(data);
}
// 获取四边形的顶点和边向量
uint3 data = gImportanceSamplingObjectDataBuffer.Load3(offset);
offset += 12;
quad.q = asfloat(data);
data = gImportanceSamplingObjectDataBuffer.Load3(offset);
offset += 12;
quad.u = asfloat(data);
data = gImportanceSamplingObjectDataBuffer.Load3(offset);
quad.v = asfloat(data);
return quad;
}
在 CPU 端还需要添加对应的根签名并创建对应的缓冲区,这里将重要性采样的几何体的添加实现在程序图元中:
// 统一管理所有的程序图元
class ProceduralGeometryManager
{
public:
struct ImportanceSamplingObject
{
RayTracing::ImportanceSampling::ImportanceSamplingPrimitiveType type = RayTracing::ImportanceSampling::Sphere;
Math::Matrix4 objToWorld{};
};
void AddImportanceSamplingObject(std::span<ImportanceSamplingObject> objs)
{
if(!objs.empty()) {
m_ImportanceSamplingObjects.insert(m_ImportanceSamplingObjects.end(), objs.begin(), objs.end());
}
}
void AddImportanceSamplingObject(ImportanceSamplingObject obj)
{
m_ImportanceSamplingObjects.push_back(std::move(obj));
}
private:
std::vector<ImportanceSamplingObject> m_ImportanceSamplingObjects{};
};
在 RayTracer 中添加对应的资源缓冲区:
class RayTracer
{
public:
...
void AddImportanceSamplingObject(std::span<ProceduralGeometryManager::ImportanceSamplingObject> objs)
{
if(objs.empty())
return;
m_ProceduralGeometryManager->AddImportanceSamplingObject(std::move(objs));
auto& objects = m_ProceduralGeometryManager->GetAllImportanceSamplingObjects();
std::vector<RayTracing::ImportanceSampling::ImportanceSamplingObject> importanceSamplingObjects{};
importanceSamplingObjects.reserve(objects.size());
std::vector<uint8_t> importanceSamplingObjectData{};
for (const auto& [type, objToWorld] : objects) {
auto offset = importanceSamplingObjectData.size();
auto dataSize = RayTracing::ImportanceSampling::ImportanceSamplingDataSize[type];
importanceSamplingObjectData.resize(offset + dataSize);
auto& object = importanceSamplingObjects.emplace_back();
object.type = type;
object.primitiveDataOffset = offset;
switch(type){
case RayTracing::ImportanceSampling::ImportanceSamplingPrimitiveType::Sphere:{
Math::Vector4 center = Math::Vector4{0,0,0,1} * objToWorld;
std::memcpy(importanceSamplingObjectData.data() + offset, ¢er, sizeof(float) * 3);
offset += sizeof(float) * 3;
float radius = objToWorld.GetX().GetX();
radius = (std::max)(radius, (float)objToWorld.GetY().GetY());
radius = (std::max)(radius, (float)objToWorld.GetZ().GetZ());
std::memcpy(importanceSamplingObjectData.data() + offset, &radius, sizeof(radius));
offset += sizeof(radius);
break;
}
case RayTracing::ImportanceSampling::ImportanceSamplingPrimitiveType::Quad:{
auto worldToObj = Math::Matrix4::Inverse(objToWorld);
std::memcpy(importanceSamplingObjectData.data() + offset, &worldToObj, sizeof(worldToObj));
offset += sizeof(worldToObj);
std::array<Math::Vector3, 3> quadData{
Math::Vector3{-1, -1, 0},
Math::Vector3{ 2, 0, 0},
Math::Vector3{ 0, 2, 0}
};
quadData[0] = Math::Vector3{Math::Vector4{quadData[0]} * objToWorld};
quadData[1] = quadData[1] * Math::Matrix3{objToWorld};
quadData[2] = quadData[2] * Math::Matrix3{objToWorld};
for(int i = 0; i < quadData.size(); ++i){
std::memcpy(importanceSamplingObjectData.data() + offset, &quadData[i], sizeof(float) * 3);
offset += sizeof(float) * 3;
}
break;
}
default:
assert(!"Unknown importance sampling primitive type");
break;
}
}
m_ImportanceSamplingObjectBuffer.Create(L"ImportanceSamplingObjectBuffer",
GpuBufferDesc{
.m_Size = sizeof(RayTracing::ImportanceSampling::ImportanceSamplingObject) * importanceSamplingObjects.size(),
.m_Stride = sizeof(RayTracing::ImportanceSampling::ImportanceSamplingObject),
.m_HeapType = D3D12_HEAP_TYPE_DEFAULT
},
importanceSamplingObjects.data());
m_ImportanceSamplingObjectDataBuffer.Create(L"ImportanceSamplingObjectDataBuffer",
GpuBufferDesc{
.m_Size = importanceSamplingObjectData.size(),
.m_Stride = 1,
.m_HeapType = D3D12_HEAP_TYPE_DEFAULT
},
importanceSamplingObjectData.data());
}
void AddImportanceSamplingObject(ProceduralGeometryManager::ImportanceSamplingObject objs)
{
AddImportanceSamplingObject({&objs, 1});
}
private:
...
GpuBuffer m_ImportanceSamplingObjectBuffer{}; // 重要性采样对象
GpuBuffer m_ImportanceSamplingObjectDataBuffer{}; // 重要性采样对象的数据
};
面光源的 PDF
首先是面光源,在渲染过程中我们对半球上的立体角进行积分计算光照贡献,因此我们需要将微分面源投影到单位半球上,可用下图进行表示:
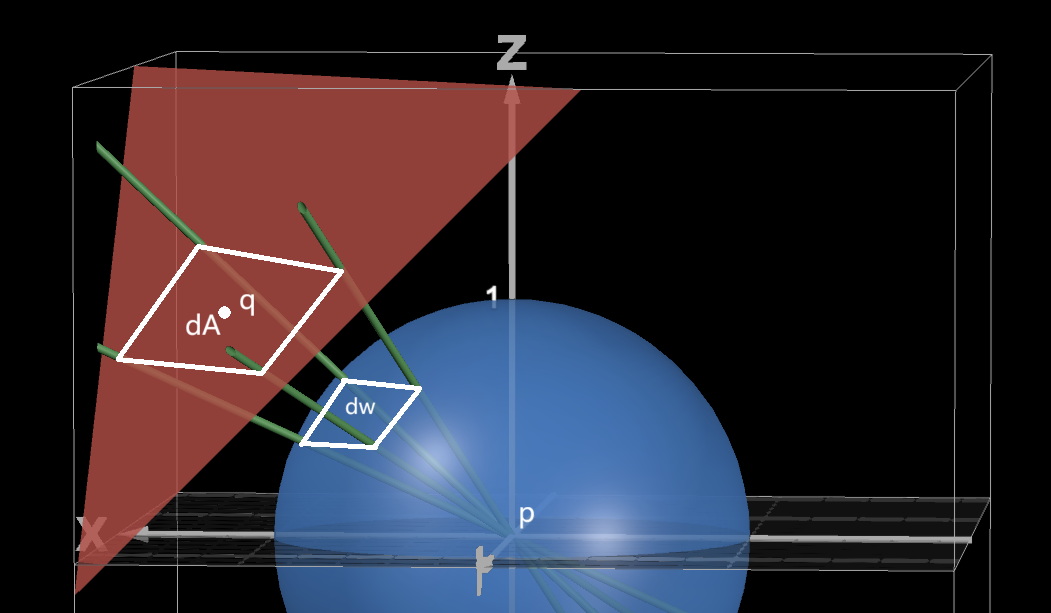
其中 \(dA\) 为面光源的面积,\(d\omega\) 为面光源投影到单位球面上的面积,由于对两者进行采样的概率相同,因此两者应满足以下关系:
其中 \(p(\omega)\) 为我们需要求的光源的 PDF,而 \(p_q(q)\) 为微分面源的 PDF,由于我们对光源进行均匀采样,因此微分面源的 PDF 为常数 \(\frac{1}{A}\) ,而 \(dA\) 和 \(d\omega\) 满足以下关系:
其中 \(\theta\) 为微分面源的法线与向量 pq 之间的夹角,\(distance^2(p, q)\) 为 p、q 两点的距离,该关系其实就是将空间中任意平面投影到单位球面的公式。将上式带入等式即可得到:
整理一下后得到以下关系:
根据该公式即可得到光源的 PDF,在代码中的具体实现如下:
float GetQuadImportanceSamplingPDF(float3 origin, float3 dir, uint primitiveDataOffset)
{
RayTracing::ImportanceSampling::QuadData quad = GetQuadData(primitiveDataOffset);
// 获取着色点到四边形的距离
Ray ray = { origin, dir };
RayTracing::ProceduralPrimitiveAttributes attributes;
float time = 0.0f;
if(!RayQuadIntersectionTest(ray, float2(MIN_RAY_LENGTH, MAX_RAY_LENGTH), quad.q, quad.u, quad.v, attributes, time)) {
return 0.0f;
}
// 从四边形上的面积投影到立体角转换到
// dw = (dA * cosθ) / (r^2)
// dA = dw * (r^2) / cosθ
float distanceSquared = time * time * dot(dir, dir);
float cosine = abs(dot(dir, attributes.normal) / length(dir));
float area = length(cross(quad.u, quad.v));
return distanceSquared / (cosine * area);
}
float GetImportanceSamplingPDF(float3 origin, float3 dir)
{
float pdfVal = 0;
const float numObjects = gSceneCB.numImportanceSamplingObjects;
if(numObjects <= 0)
return pdfVal;
float weight = 1.0f / numObjects;
for(uint i = 0; i < (uint)numObjects; i++)
{
float val = 0;
RayTracing::ImportanceSampling::ImportanceSamplingObject obj = gImportanceSamplingObjects[i];
switch(obj.type){
case RayTracing::ImportanceSampling::ImportanceSamplingPrimitiveType::Sphere: {
val = GetSphereImportanceSamplingPDF(origin, dir, obj.primitiveDataOffset);
break;
}
case RayTracing::ImportanceSampling::ImportanceSamplingPrimitiveType::Quad: {
val = GetQuadImportanceSamplingPDF(origin, dir, obj.primitiveDataOffset);
break;
}
default:
val = 0.0f;
break;
}
pdfVal += val * weight;
}
return pdfVal;
}
这里的GetImportanceSamplingPDF遍历了所有重要性采样几何体,计算其 PDF 并取其均值。在获取 PDF 的函数GetPDFValue中将其添加进去:
float GetPDFValue(PDFType pdfType, Ray incomingRay, Ray scatterRay, Surface surface)
{
switch(pdfType) {
case PDFType::ImportanceSamplingPDF: {
return GetImportanceSamplingPDF(scatterRay.origin, scatterRay.direction);
}
...
default:
return 0.0f;
}
}
实现面光源的 PDF 还没完,还需要实现符合该 PDF 分布的采样,由于面光源投影到半球上后都是均匀的,因此采样较为简单,只需要在面光源上随机选择一个点,物体表面和随机点的连线即为符合面光源的 PDF 的采样点。具体实现如下:
float3 SampleQuadImportanceSamplingPDF(float3 origin, uint primitiveDataOffset, inout PCGState rng)
{
RayTracing::ImportanceSampling::QuadData quad = GetQuadData(primitiveDataOffset);
// 在四边形上随机取一个点
float3 p = quad.q + (RandomFloat(rng) * quad.u) + (RandomFloat(rng) * quad.v);
return p - origin;
}
float3 SampleImportanceSamplingPDF(float3 origin, inout PCGState rng)
{
uint size = gSceneCB.numImportanceSamplingObjects;
if(size <= 0)
return 0;
uint index = RandomUint(rng, 0, size - 1);
RayTracing::ImportanceSampling::ImportanceSamplingObject obj = gImportanceSamplingObjects[index];
switch(obj.type){
case RayTracing::ImportanceSampling::ImportanceSamplingPrimitiveType::Quad: {
return SampleQuadImportanceSamplingPDF(origin, obj.primitiveDataOffset, rng);
}
...
default:
return 0;
}
}
float3 SamplePDF(PDFType pdfType, Surface surface, inout PCGState rng)
{
switch(pdfType) {
case PDFType::ImportanceSamplingPDF: {
return SampleImportanceSamplingPDF(surface.position, rng);
}
...
default:
return 0;
}
}
将函数GetColor中的scatterRecord.pdfType更改为PDFType::ImportanceSamplingPDF,最后得到的结果如下:
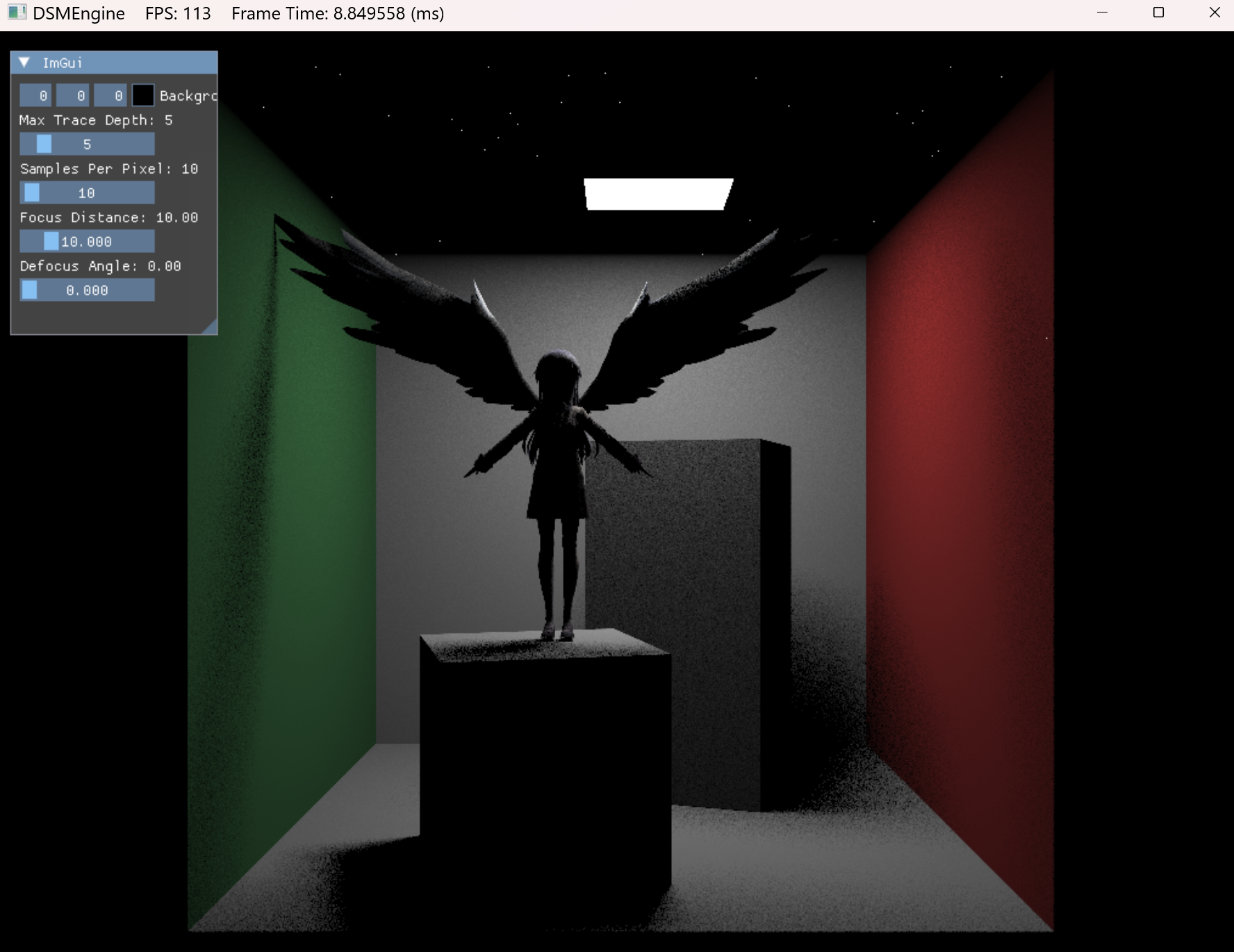
可以看到使用了重要性采样后仅仅10 spp 就可以得到噪声这么低的画面,但是不足之处也含明显,光照无法直接照到的位置都为全黑,因此通常使用多种 PDF 的混合。现在实现的对光源的重要性采样其实和上一篇文章的 ShadowRay 思想其实很类似,上一篇的 ShadowRay 是沿着方向光的方向追踪光线并判断是否遮挡,而重要性采样则是沿着各种光源的方向追踪光线并获取颜色,所以对于光源无法直接照射的位置无法获得间接光照,只能获取来自光源的直接光照。
球光源的 PDF
对于球形的光源,选取采样点的时候就不能简单的在球面上选取一个点,因为将球投影到单位球面上是不均匀的,为了均匀的在可见范围内采样球体,需要将其等效为在球对应的立体角上的均匀采样,具体的推导过程可阅读 RayTracingInOneWeekend,实现如下:
// 正交基变换
float3 OrthonormalBasisTransform(float3 normal, float3 dir)
{
normal = normalize(normal);
float3 a = abs(normal.x) > 0.9 ? float3(0, 1, 0) : float3(1, 0, 0);
float3 tangent = normalize(cross(normal, a));
float3 bitangent = cross(normal, tangent);
float3x3 TBN = float3x3(bitangent, tangent, normal);
dir = dir[0] * TBN[0] + dir[1] * TBN[1] + dir[2] * TBN[2];
return dir;
}
// 球体的重要性采样
float GetSphereImportanceSamplingPDF(float3 origin, float3 dir, uint primitiveDataOffset)
{
RayTracing::ImportanceSampling::SphereData sphere = GetSphereData(primitiveDataOffset);
// 需要变换到对象空间进行相交检测
Ray ray = {origin, dir};
float time = 0.0f;
float3 oc = sphere.center - ray.origin;
float a = dot(ray.direction, ray.direction);
float h = dot(ray.direction, oc);
float c = dot(oc, oc) - sphere.radius * sphere.radius;
float discriminant = h * h - a * c;
if (discriminant < 0) { // 没有根则不相交
return false;
}
float sqrtD = sqrt(discriminant);
time = (h - sqrtD) / a; // 计算方程的根
if (time <= MIN_RAY_LENGTH || time >= MAX_RAY_LENGTH) { //不再范围内
// 由于生成随机向量时只考虑了球外的情况,因此不需要检测是否球内相交
return false;
}
// 计算立体角
float3 rayToCenter = sphere.center - origin;
float distSquared = dot(rayToCenter, rayToCenter);
float cosThetaMax = sqrt(1 - sphere.radius * sphere.radius / distSquared);
float solidAngle = 2 * s_PI * (1 - cosThetaMax);
return 1.0f / solidAngle;
}
// 球体的重要性采样
float3 SampleSphereImportanceSamplingPDF(float3 origin, uint primitiveDataOffset, inout PCGState rng)
{
RayTracing::ImportanceSampling::SphereData sphere = GetSphereData(primitiveDataOffset);
float3 direction = sphere.center - origin;
float distanceSquared = dot(direction, direction);
float r1 = RandomFloat(rng);
float r2 = RandomFloat(rng);
float cosThetaMax = sqrt(1 - sphere.radius * sphere.radius / distanceSquared);
float z = 1 + r2 * (cosThetaMax - 1);
float sinTheta = sqrt(1 - z * z);
float phi = 2 * s_PI * r1;
float x = cos(phi) * sinTheta;
float y = sin(phi) * sinTheta;
float3 sampleDir = float3(x, y, z);
return OrthonormalBasisTransform(direction, sampleDir);
}
混合 PDF
由于只对光源进行重要性采样无法获得间接光照,因此最终使用的 PDF 除了重要性采样的 PDF 还有物体表面本身的 PDF,最后结果为两者的线性混合,而样本点则是随机从两者中选择一个,具体实现如下:
// Mixture PDF
float GetMixturePDFValue(PDFType pdfTypes[2], Ray incomingRay, Ray scatterRay, Surface surface)
{
float pdf1 = GetPDFValue(pdfTypes[0], incomingRay, scatterRay, surface);
float pdf2 = GetPDFValue(pdfTypes[1], incomingRay, scatterRay, surface);
return 0.5f * (pdf1 + pdf2);
}
float3 SampleMixturePDF(PDFType pdfTypes[2], Surface surface, inout PCGState rng)
{
PDFType selectedPDF = RandomFloat(rng) < 0.5f ? pdfTypes[0] : pdfTypes[1];
return SamplePDF(selectedPDF, surface, rng);
}
在进行渲染的函数GetColor中要进行如下修改:
float4 GetColor(inout RayTracing::RayPayload payload, Surface surface)
{
...
if(scatterRecord.skipPDF) {
...
}
else{
// 使用混合 PDF 进行采样,一个是与物体表面 BRDF 相关的 PDF,一个是重要性采样 PDF
PDFType pdfTypes[2] = {scatterRecord.pdfType, scatterRecord.pdfType};
if(gSceneCB.numImportanceSamplingObjects > 0) {
pdfTypes[1] = PDFType::ImportanceSamplingPDF;
}
// 根据 pdf 进行采样
float3 pdfSampleDir = SampleMixturePDF(pdfTypes, surface, payload.rng);
Ray scatterRay;
scatterRay.origin = surface.position;
scatterRay.direction = pdfSampleDir;
// 获取材质的 PDF
float pdfVal = GetMixturePDFValue(pdfTypes, incomingRay, scatterRay, surface);
// 材质在特定方向进行散射的概率
float scatterPDF = GetScatteringPDF(lMaterialCB.type, incomingRay, scatterRay, surface);
color = TraceRadianceRay(scatterRay, payload.depth, payload.rng);
color = (color * float4(scatterRecord.attenuation, 1) * scatterPDF) / pdfVal;
}
color.rgb += scatterRecord.emission;
return color;
}
添加完混合 PDF 的结果如下:
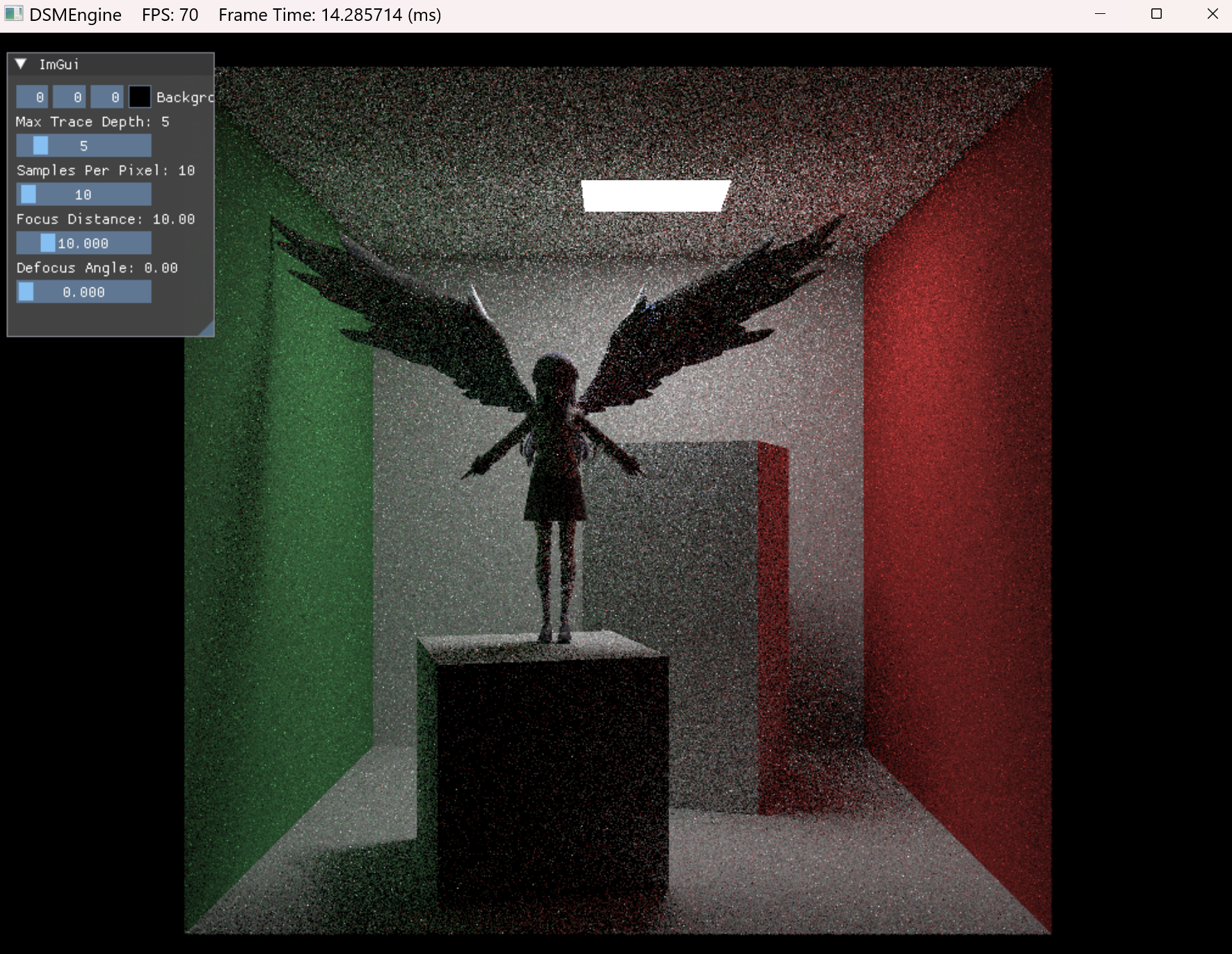
可以看到虽然噪声变多了,但是暗处有了间接光。至此使用 DXR 实现 RayTracingInOneWeekend 也算大致完成了,项目源码可从此处获取:LearnMiniEngine/Samples/RayTracingInOneWeekend



 浙公网安备 33010602011771号
浙公网安备 33010602011771号