归并排序(Merge sort)
归并排序(Merge sort)
基本概念
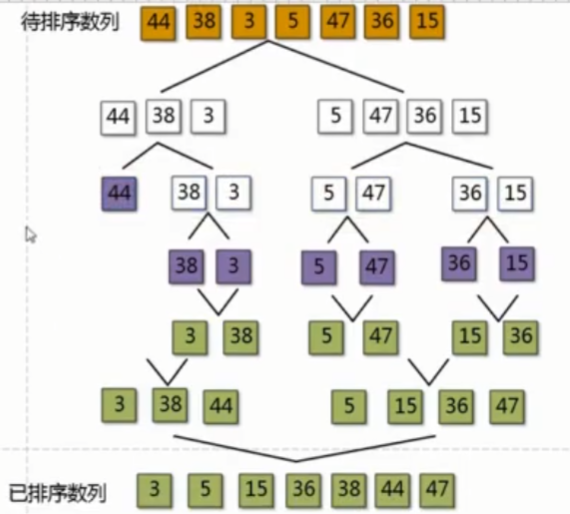
归并排序是一种高效且稳定的排序算法,其采用的方法是分治法(Divide and Conquer),即分而治之。归并排序的基本思想即分离后合并,每次分离将全部元素分为两个子序列,直到分离到一个序列只剩一个元素为止,分离完成后,按照原先分离的顺序合并已经有序的子序列,因为只有一个元素时必定是有序的,所以递归分离后所有子序列都是有序的。
实现步骤:
- 根据二分法分离数据,到一个序列只剩一个元素为止。
- 比较每个有序序列的元素,将其分配到辅助空间中。
- 将重复步骤二,最后所有有序序列合并为完整的有序序列
示例图:
性质
时间复杂度
每次归并都是将序列分为两部分,直到只剩一个元素,再合并,归并过程需要\(logN\)次,每次归并又需要进行最多\(N-1\)次比较,最少需要\(\frac{N}{2}\)次比较,因此归并排序的时间按复杂度为\(O(NlogN)\)。
空间复杂度
在归并排序的合并阶段,需要将已排序的子序列放置在临时的空间中,因此需要大小与原数据相等的额外空间,所有空间复杂度为\(O(N)\)。
稳定性
以正序排序为例,每次每次比较不仅要判断左子序列的元素是否小于右子序列的元素,还要判断是否相等,由此才不会改变相同元素的相对位置,归并排序才是稳定的。
实现
数组实现
template <typename T>
inline void SeparateAndMerge(T* const ptr, std::vector<T>& tmpData, size_t left, size_t right, bool cmp(const T*, const T*))
{
//分离到只剩一个后递归停止
if (left < right) {
//中间索引
size_t mid = (left + right) / 2;
//左侧分离
SeparateAndMerge(ptr, tmpData, left, mid, cmp);
//右侧分离
SeparateAndMerge(ptr, tmpData, mid + 1, right, cmp);
//分离后合并
size_t lpos = left, rpos = mid + 1;
//合并前后的下标
size_t pos = left;
for (; lpos <= mid && rpos <= right;) {
//若返回true取右侧,也就是左侧大于右侧
if (cmp(ptr + lpos, ptr + rpos)) {
tmpData[pos++] = *(ptr + rpos++);
}
else {
tmpData[pos++] = *(ptr + lpos++);
}
}
//左侧剩余
for (; lpos <= mid;) {
tmpData[pos++] = *(ptr + lpos++);
}
//右侧剩余
for (; rpos <= right;) {
tmpData[pos++] = *(ptr + rpos++);
}
std::memmove(ptr + left, tmpData.data() + left, (right - left + 1) * sizeof(T));
//使用std::mommove好像更快一点
//std::copy(tmpData.data() + left, tmpData.data() + right + 1, ptr + left);
}
}
template <typename T>
inline void MergeSort(T* const ptr, const size_t count, bool cmp(const T*, const T*) = DefaultCmp)
{
if (!count || !ptr) {
return;
}
//储存分离后合并的数据
std::vector<T> tmpData;
tmpData.reserve(count);
tmpData.resize(count, T(*ptr));
//递归分离
SeparateAndMerge(ptr, tmpData, 0, count - 1, cmp);
}
其中tmpData为需要的辅助空间,这里使用STL中的vector容器方便管理,使用reserve方法来避免扩容时的开销:
std::vector<T> tmpData;
tmpData.reserve(count);
tmpData.resize(count, T(*ptr));
SeparateAndMerge为递归分离与合并的主函数每次分别对左侧和右侧进行分离:
//中间索引
size_t mid = (left + right) / 2;
//左侧分离
SeparateAndMerge(ptr, tmpData, left, mid, cmp);
//右侧分离
SeparateAndMerge(ptr, tmpData, mid + 1, right, cmp);
使用循环来合并排序子序列,每次将其中一个子序列的元素放入辅助空间:
for (; lpos <= mid && rpos <= right;) {
//若返回true取右侧,也就是左侧大于右侧
if (cmp(ptr + lpos, ptr + rpos)) {
tmpData[pos++] = *(ptr + rpos++);
}
else {
tmpData[pos++] = *(ptr + lpos++);
}
}
//左侧剩余
for (; lpos <= mid;) {
tmpData[pos++] = *(ptr + lpos++);
}
//右侧剩余
for (; rpos <= right;) {
tmpData[pos++] = *(ptr + rpos++);
}
最后更新原始数据:
std::memmove(ptr + left, tmpData.data() + left, (right - left + 1) * sizeof(T));
单链表实现
单链表的实现核心思想与数组也是一样的,将所有元素拆分为左右两边,分别排序后合并,但是单链表的归并排序即使不使用复杂的优化也能做到\(O(1)\)的空间消耗。
排序的主体部分与数组相同,毕竟算法核心不变:
ListNode* MergeSort(ListNode* begin, ListNode* end)
{
assert(begin != nullptr && end != nullptr);
if (begin == end) { // 只有一个节点将后续置空方便合并
if (begin != nullptr) begin->next = nullptr;
return begin;
}
ListNode* mid = FindMid(begin, end);
auto midNext = mid->next;
begin = MergeSort(begin, mid);
mid = MergeSort(midNext, end);
// 此时begin和mid都为独立的链表
return Merge(begin, mid);
}
其中不同的是达到递归的终止条件时我把元素的下一个节点置空了,这是为了让其成为一个独立的链表,方便后续合并的终止判断。同时与数组的直接 (end - begin) / 2 不同,链表的中间节点需要额外查找,查找方法使用的快慢指针法,慢指针会成为指向中点的指针:
ListNode* FindMid(ListNode* begin, ListNode* end)
{
assert(begin != nullptr && end != nullptr);
ListNode* slow = begin;
for (ListNode* fast = begin; fast != end && fast->next != end; slow = slow->next, fast = fast->next->next);
return slow;
}
其中Merge函数也与普通实现不同,数组实现是将合并好的元素放在额外的数组中,而由于链表的特性,可直接在合并时将排序好的节点链接成新的链表,只需要创建一个额外的节点作为头节点即可,具体实现如下:
ListNode* Merge(ListNode* head0, ListNode* head1)
{
assert(head0 != nullptr && head1 != nullptr);
auto tmpHead = std::make_shared<ListNode>(0, nullptr);
ListNode* tmp = tmpHead.get();
ListNode* tmp0 = head0, * tmp1 = head1;
auto changeTmp = [](auto& tmp, auto& node) {
tmp->next = node;
tmp = node;
node = node->next;};
while (tmp0 != nullptr && tmp1 != nullptr) {
if (tmp0->val < tmp1->val) {
changeTmp(tmp, tmp0);
}
else {
changeTmp(tmp, tmp1);
}
}
for (auto node = tmp0 == nullptr ? tmp1 : tmp0; node != nullptr; ) {
changeTmp(tmp, node);
}
return tmpHead->next;
}
传入的参数为两个独立的链表,由于先前达到终止条件时让每个节点都成为独立的链表,因此合并后的链表依然是独立的链表,这样省去了复杂的条件判断。
完整代码如下:
class ForwardListMergeSort
{
public:
ListNode* SortList(ListNode* head)
{
if (head == nullptr || head->next == nullptr) return head;
// write code here
// 获取最后一个节点
auto tail = head;
for (; tail->next != nullptr; tail = tail->next);
return MergeSort(head, tail);
}
private:
ListNode* MergeSort(ListNode* begin, ListNode* end)
{
assert(begin != nullptr && end != nullptr);
if (begin == end) { // 只有一个节点将后续置空方便合并
if (begin != nullptr) begin->next = nullptr;
return begin;
}
ListNode* mid = FindMid(begin, end);
auto midNext = mid->next;
begin = MergeSort(begin, mid);
mid = MergeSort(midNext, end);
// 此时begin和mid都为独立的链表
return Merge(begin, mid);
}
ListNode* Merge(ListNode* head0, ListNode* head1)
{
assert(head0 != nullptr && head1 != nullptr);
auto tmpHead = std::make_shared<ListNode>(0, nullptr);
ListNode* tmp = tmpHead.get();
ListNode* tmp0 = head0, * tmp1 = head1;
auto changeTmp = [](auto& tmp, auto& node) {
tmp->next = node;
tmp = node;
node = node->next;};
while (tmp0 != nullptr && tmp1 != nullptr) {
if (tmp0->val < tmp1->val) {
changeTmp(tmp, tmp0);
}
else {
changeTmp(tmp, tmp1);
}
}
for (auto node = tmp0 == nullptr ? tmp1 : tmp0; node != nullptr; ) {
changeTmp(tmp, node);
}
return tmpHead->next;
}
ListNode* FindMid(ListNode* begin, ListNode* end)
{
assert(begin != nullptr && end != nullptr);
ListNode* slow = begin;
for (ListNode* fast = begin; fast != end && fast->next != end; slow = slow->next, fast = fast->next->next);
return slow;
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号