着色（Shading）

着色（Shading）

Blinn-Phong 反射模型（Blinn-Phong Reflectance Model）

Blinn-Phong 反射模型将光分为三种：

1. 反射高光（Specular Highlights）。
2. 漫反射（Diffuse Reflection）。
3. 环境光（Ambient Lighting）。

漫反射（Diffuse Reflection）

漫反射的定义：
一个光线打到物体的一个点时，光线被均匀的反射到各个方向。

朗伯余弦定律（Lambert's cosine law）：

假设平面接收的光照是固定的，

那么当平面倾斜是所接收到的光就会减少，

朗伯余弦定律定义了：接收的光强与光线方向I和法线n的夹角的余弦值成正比!

这就是物体接收光的模型。

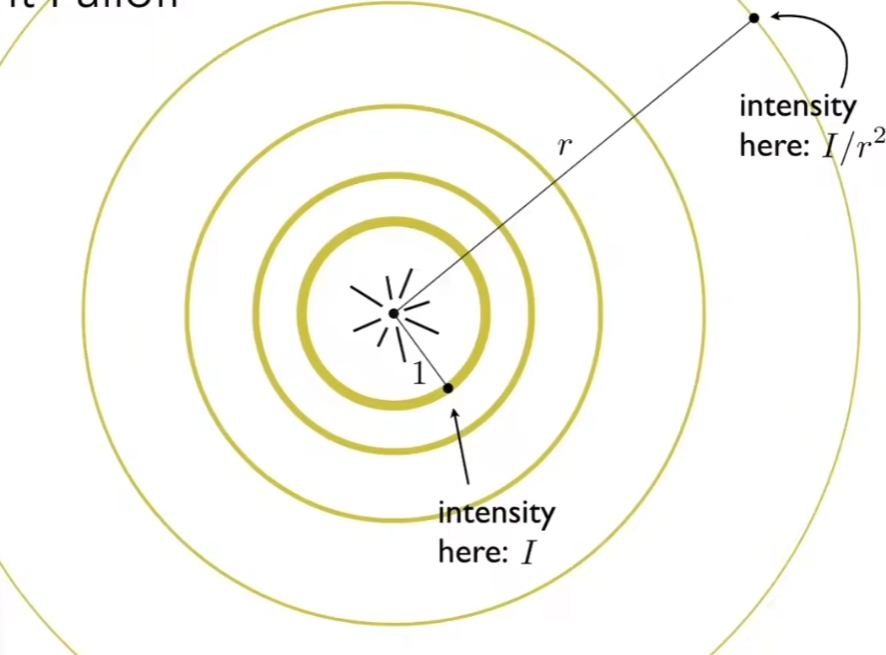
Light Fallof

可以把光源的传播看成一个球壳，沿着一个方向光的强度逐渐下降。

也就是物体能接收到的光的能量与距离成反比，这就是光发射传播的模型。

由此就可以得出漫反射的光照模型：

其中I为单位距离上光的强度，r为反射点到接收点的距离。
在HLSL中表面到光源的向量使用如下语句计算：

float3 lightVec = L.position - pos;	//光的位置减去顶点的位置

表面到光线的距离使用HLSL中的length函数计算：

float r = length(lightVec);

所以\(I/r^2\)就是光到达着色点的能量。\(max(0,n\cdot l)\),就是朗伯余弦定理，表示着色点接受的能量，其中max()是为了除去反方向的光，在HLSL中如下计算：

float diffuseFactor = dot(lightVec, normal);
if (diffuseFactor > 0.0f) {}

\(k_d\)表示漫反射系数，也就是该着色点反射出去的能量。最后把这几个因素相乘就可以得到漫反射的结果：

diffuse = diffuseFactor * mat.diffuse * L.diffuse;

镜面反射（Specular Term）

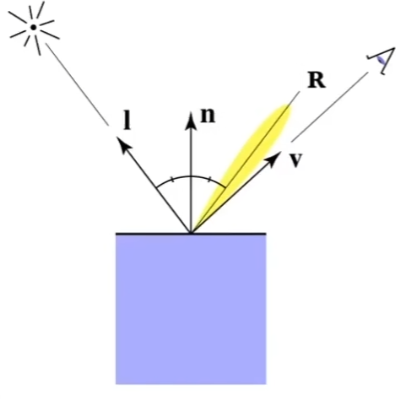
定义当观察方向与镜面反射方向接近时可以看到高光，也就是向量\(R\)与向量\(v\)之间的夹角较小时才能看到高光，当向量\(R\)与向量\(v\)接近时，法线方向\(n\)与半程向量\(h\)（向量\(l\)和向量\(v\)的角平分线上的单位向量）也接近，由此就可以通过这两者判断来判断镜面反射，使用半程向量是因为半程向量比反射方向要好计算。

其中Phong反射模型就使用了求出光线反射后再用反射向量点乘向量v，在HLSL中使用了如下代码：

//reflect返回反射向量，这里可以用Blinn-Phong模型，从而不需要使用reflect函数
float3 v = reflect(-lightVec, normal); 

其中\(I/r^2\)与漫反射相同，通过\(n \cdot h\)来判断是否能看到高光，\(k_s\)为镜面反射系数，通常表示白色。

其中\(max(0,n \cdot h)\)还要加上p这个系数是因为高光通常很小，而\(n \cdot h\)之后的cos值下降趋势比较小，会导致高光很大，加上指数p就可以增大下降趋势，减小高光大小，p通常在100至200之间。

漫反射加上高光的效果：

环境光（Ambient Term）

由于环境光过于复杂，因此模型将环境光表示为光照下的任何一个点收到的环境光相同，环境光不受光照方向和观察方向的影响，是一个常数，表示为：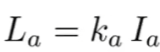

最后三种光照相叠加既是Blinn-Phong 反射模型：