李宏毅深度学习笔记-结构化线性模型

之前讲了三个问题，现在就要想办法解这三个问题。

假如第一个问题有某种特殊的形式（\(F(x,y)\)长某个样子），那第三个问题就不是个问题。

所以先来讲讲看special form应该长什么样子。这个special form必须是Linear的，给我一个\((x,y)\)的pair，首先我用一组特征来描述\((x,y)\)的pair，每个\(\phi_i\)代表一个value（一个标量，代表特征的强度值），具有特征1的强度是\(\phi_1(x,y)\)，具有特征2的强度是\(\phi_2(x,y)\)......。

\(F(x,y)\)长什么样子呢？

定义为\(F(x,y)=w_1 \cdot \phi_1(x,y)+w_2\cdot \phi_2(x,y)+w_3\cdot \phi_3(x,y)...\)，\(w_1,w_2,w_3\)是从训练数据中学习的，可以写成向量形式\(F(x,y)={\bf{x}^T}{\bf{\phi}}(x,y)\)。接下来要将的就是，假如\(F(x,y)\)写成这样，那问题3就不是一个问题。

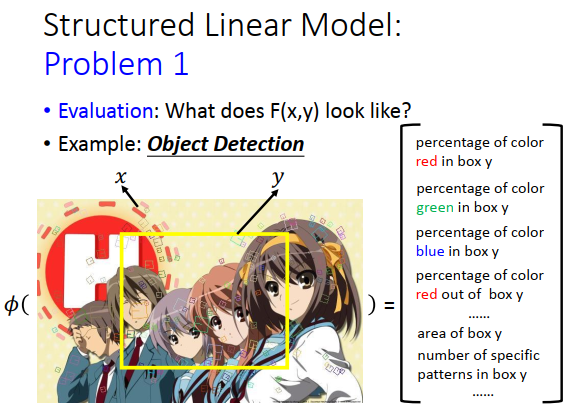
举例子讲一个\(F(x,y)\)长什么样子。

比如我们要做目标检测，\(x\)是图片，\(y\)是一个bounding box，我要定义一个特征的向量\(\phi\)，\(\phi\)把x（图片）和y（bounding box）代进\(\phi\)这个函数里面，我们要得到一个向量。

这个向量怎么定呢？

随便自己定义，比如红色pixel在黄色框框里出现的百分比是一个维度，绿色pixel在黄色框框里出现的百分比是一个维度，蓝色pixel在黄色框框里出现的百分比是一个维度，红色在框框外的百分比又是一个维度，框框大小是一个维度。但是这个特征很弱，可能没办法做凉宫春日的检测。现在在image中比较state-of-the-art 可能是用visual work，visual work就是图片上的小方框片，每一个方块都代表了某种pattern，不同颜色的方块代表不同的pattern，就像文章里的词汇一样，所以叫做visual work。你就可以说，在这个框框里面，编号是100号的visual work出现了几个，就是一个维度的特征。

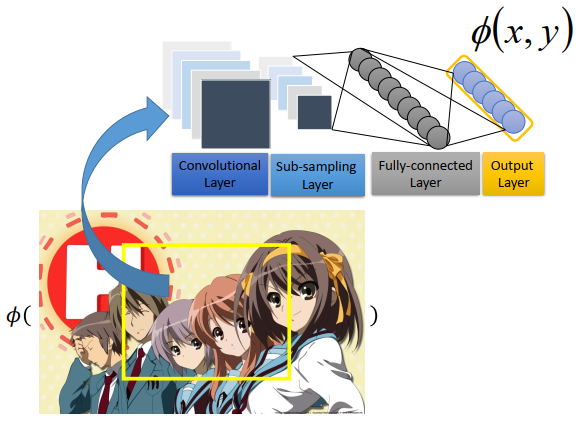
这些特征要由人找出来的吗？还是我们直接用一个model来抽呢？

我们现在定义的\(F(x,y)\)是一个线性函数，是两个向量的内积，那就没办法做太厉害的事情。如果要让

最后performer好的话，就需要抽出很好的特征。用人工抽取的方法，不见得能找出好的特征，所以是在目标检测这个task上面，state-of-the-art 方法是，例如去训练一个CNN。你可以把图片丢进CNN里面，会output出一个向量，这个向量可以很好的去代表这个bounding box里面的东西。 目标检测不能用一般的深度神经网络做，没办法告诉你框框在哪，其实是用深度神经网络+结构化学习的方法做的，所以抽特征可以用深度学习来做。

如果做摘要抽取的话，\(x\)是一个document，也是一个summary。你可以定一些特征，比如\(\phi_1\)（\(y\)里面有没有包含"important"，包含为1，反之为0），这个特征的权重可能比较大，因为包含“important”的话\(y\)可能是一个合理的summary。或者是\(\phi_2\)（\(y\)里面有没有包含"definition"），或者\(\phi_3\)（\(y\)的长度是多少），你可以定义各种各样的特征，或者你可以定义一个evaluation说\(y\)的精简程度是多少等等，也可以想办法用deep learning抽一些比较有用的特征。

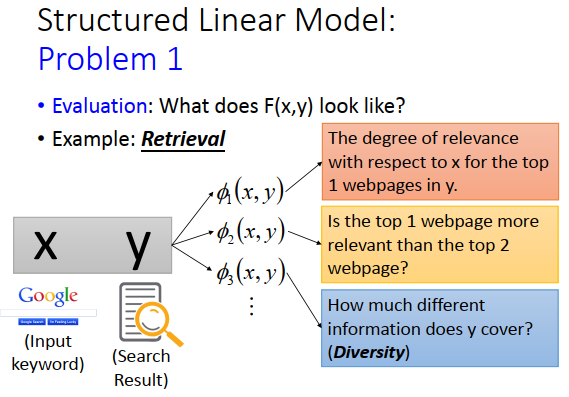
如果是搜索的话，也是一样的。\(x\)是keyword，y是搜寻的结果。比如你定义\(\phi_1\)（\(y\)的第一笔搜索结果和\(x\)的相关程度），或者\(\phi_2\)（\(y\)的第一笔搜索结果和\(x\)的相关程度有没有比第二笔搜索结果高），也可以定\(\phi_3\)（y的Diversity的程度是多少）。我们知道说每个人想找的东西都不一样，比如你输入java（想学一些和java有关的东西），那搜索引擎不知道你要找的到底是什么，那一个好的方法就是把各种信息都找出来，所以可以定义Diversity，看搜索结果是不是包含足够不同、丰富的信息。

这些就是第一个问题，就是想办法定义特征。

第一个问题定义好了以后，\(F(x,y)\)可以写成\(F(x,y)=w\cdot \phi(x,y)\)（两个向量的内积），一样的要去穷举所有的\(y\)，看哪一个\(y\)可以让\(F(x,y)\)最大。

这个怎么办呢？我们先假设这个问题已经被解决了。

假装第二个问题解决后，进入第三个问题。今天找了一大堆训练数据\(\{x,\hat y\}\)，我希望找到一个函数\(F\)（其实是希望找一个\(\bf{w}\)，\(F\)是由\(\bf{w}\)定义的），使得上图最下方的条件满足。对所有数据而言，正确的\(w\cdot \phi(x^r,\hat{y}^r)\)应该大过所有其他的\(w\cdot \phi(x^r,y)\)(\(\hat y\)以外的\(y\))。

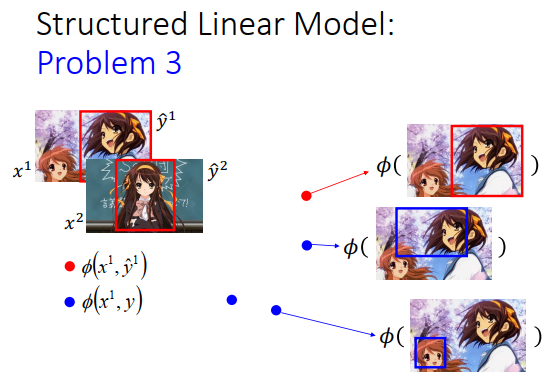
用具体的例子说明一下。

假设现在要做的是目标检测，收集了一张图片\(x^1\)，并知道对应的\(\hat y^1\)（上图左上方红色框框），又收集了另外一张图片\(x^2\)，也知道对应的\(\hat y^2\)。假设\(x^1,\hat y^1\)所形成的的特征是上图左边红色的点\(\phi(x^1,\hat y^1)\)，其他\(y\)和\(x^1\)所形成的的特征是蓝色的点\(\phi(x^1,y)\)，这里假设只有两个特征，实际上你可以抽千维万维。

我们把它画在图上（上图右边所示），如果框框在正确的地方，就是红色的点，在其他地方都是蓝色的点，所以红色的点就只有一个，蓝色的点有很多。

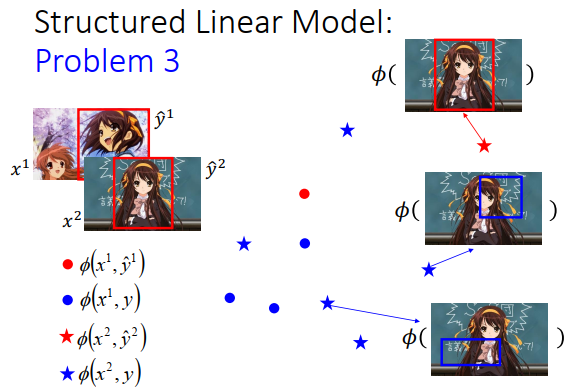
\(x^2,\hat y^2\)所形成的特征是红色的星星，\(x^2\)和其他\(y\)所形成的的特征是蓝色的星星，把红色星星和蓝色星星画在图上如上图右边所示。红色正确框框是正确的，蓝色框框是错误的。所以红色的星星只有一个，蓝色的星星有很多个。

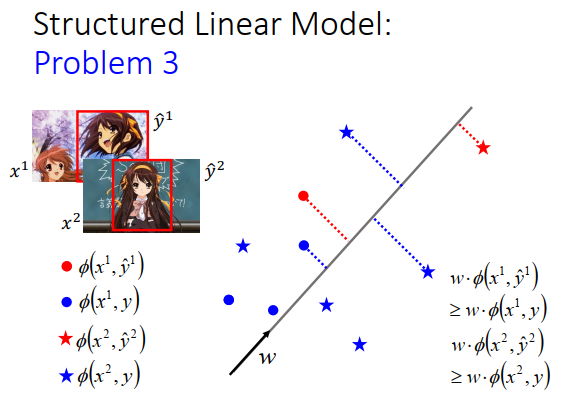
我们要达到的任务是，希望找到一个\(w\)，那这个\(w\)可以做到什么事呢？

我们把这上面的每个点，红色的星星，红色的圈圈，成千上万的蓝色圈圈和蓝色星星，统统拿去跟\(w\)做内积之后，红色星星得到的值大过所有蓝色星星得到的值，红色圈圈得到的值大过所有蓝色圈圈得到的值，当然不同形状间不比较（圈圈跟圈圈比，星星跟星星比）。也就是说我们希望正确答案所形成的的特征\(\phi(x^1,\hat y^1)\)跟\(w\)做内积后，大过其他\(\phi(x^1,y)\)跟\(w\)的内积。

我们有办法找到\(w\)吗？

这个问题并不难，以下就提供一个演算法。

假设我刚才说的那个要让红色的大于蓝色的vector，只要它存在，用上面这个演算法可以找到答案。

input：训练数据\(\{(x,\hat y)\}\)

output：一个权重向量\(w\)，要满足我们之前找到的特性

算法初始化：令\(w=0\)

​ do

​ 每次都取出一笔训练数据\((x^r,\hat y^r)\)

​ 找一个\(\hat y^r\)最大化\(w\cdot \phi(x^r,y)\)

​ \(\large \widetilde{y}^r=arg\max\limits_{y\in Y} w\cdot \phi(x^r,y)\)（这个问题其实就是问题2，我们之前假设已经解决）

​ 如果\(\large \widetilde{y}^r\)不是正确答案 \(\large \hat{y}^r\)（说明\(w\)不是我们要的，更新\(w\)）

​ \(\large w \to w+\phi(x^r,\hat y^r)-\phi(x^r,\widetilde y^r)\) （把\(\large x\)和\(\large \hat y\)的特征算出来，把\(\large x\)和\(\large \widetilde y\)的特征也算出来， 两个特征相减，再加到\(\large w\)里面）

​ 有新的\(\large w\)之后，重新计算\(\large \widetilde{y}^r\)

​ 直到\(\large w\)不再更新（如果要找的$ \large w$存在的话，最终会停止）

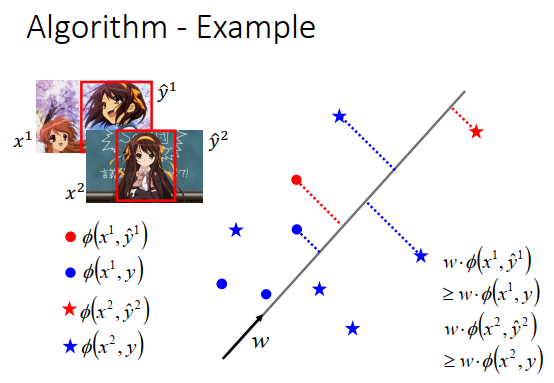
举个例子看看算法是怎么运作的。

我们的目标是要找到一个\(w\)，可以让红色星星大过蓝色星星，红色圈圈大过蓝色圈圈，假设这个\(w\)是存在的。

• 首先我们假设\(w=0\)，然后我们随便pick一个样本\(\large (x^1,\hat y^1)\)，点分布如上图红色点。
• 然后根据手上的数据和\(\large w\)，去看说哪一个\(\large y\)和\(\large x\)形成的特征跟\(\large w\)做内积后得到的值最大。现在因为\(w=0\)，不管哪个\(\large y\)算出来的值都是一样的，那我们就随机选一个\(\large y\)当做\(\large \widetilde{y}^1\)（选择的点如上图所示）。
• \(\large \widetilde{y}^1\)和\(\large \hat y^1\)不一样，所以调整一下\(\large w\) （\(\phi(x^1,\hat y^1)-\phi(x^1,\widetilde y^1)\)是上图黑色的向量）

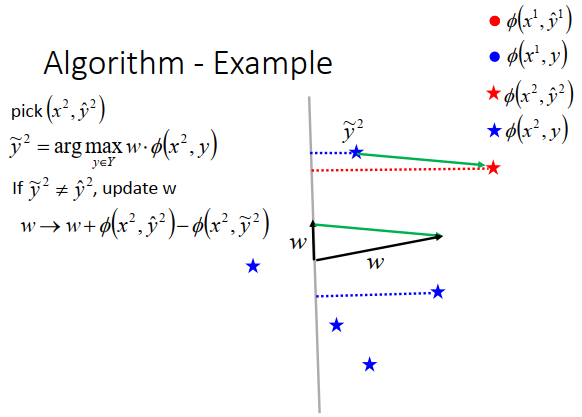
第二部再选一个样本\(\large (x^2,\hat y^2)\)

穷举所有\(\large y\) ，找出\(\large \widetilde{y}^2\)（如上图所示）

更新\(\large w\) （\(\phi(x^2,\hat y^2)-\phi(x^2,\widetilde y^2)\)就是上图绿色的向量，然后加上第一步黑色向量得到新的\(\large w\)）

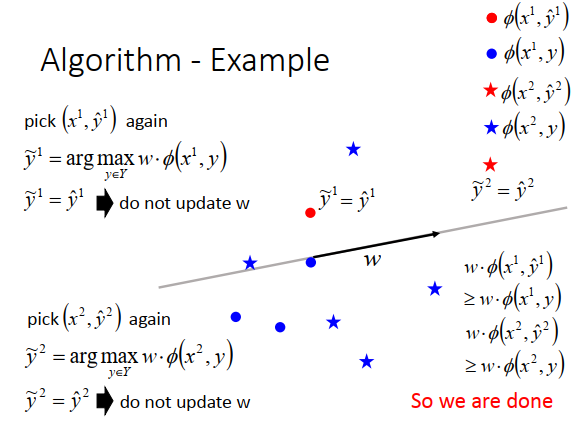
得到新的\(\large w\)以后，要再算一遍\(\large (x^1,\hat y^1)\)，跟所有的点算内积后，这时候\(\large \hat y^1=\widetilde{y}^1\) ，\(\large w\)对第一笔数据来说就是我们要对。

接下来再计算一遍\(\large (x^2,\hat y^2)\)，发现\(\large \hat y^2=\widetilde{y}^2\)，这个\(\large w\)也是我们要的。

看过所有数据之后，发现\(w\)不再更新，那么停止整个训练。