数据结构及算法(数据结构篇)



1.1.1 顺序表的实现

顺序表的代码实现: //顺序表代码 public class SequenceList<T> { //存储元素的数组 private T[] eles; //记录当前顺序表中的元素个数 private int N; //构造方法 public SequenceList(int capacity){ eles = (T[])new Object[capacity]; N=0; } //将一个线性表置为空表 public void clear(){ N=0; } //判断当前线性表是否为空表 public boolean isEmpty(){ return N==0; } //获取线性表的长度 public int length(){ return N; } //获取指定位置的元素 public T get(int i){ if (i<0 || i>=N){ throw new RuntimeException("当前元素不存在!"); } return eles[i]; } //向线型表中添加元素t public void insert(T t){ if (N==eles.length){ throw new RuntimeException("当前表已满"); } eles[N++] = t; } //在i元素处插入元素t public void insert(int i,T t){ if (i==eles.length){ throw new RuntimeException("当前表已满"); } if (i<0 || i>N){ throw new RuntimeException("插入的位置不合法"); } //把i位置空出来,i位置及其后面的元素依次向后移动一位 for (int index=N;index>i;index--){ eles[index]=eles[index-1]; } //把t放到i位置处 eles[i]=t; //元素数量+1 N++; } //删除指定位置i处的元素,并返回该元素 public T remove(int i){ if (i<0 || i>N-1){ throw new RuntimeException("当前要删除的元素不存在"); } //记录i位置处的元素 T result = eles[i]; //把i位置后面的元素都向前移动一位 1.1.2 顺序表的遍历 一般作为容器存储数据,都需要向外部提供遍历的方式,因此我们需要给顺序表提供遍历方式。 for (int index=i;index<N-1;index++){ eles[index]=eles[index+1]; } //当前元素数量-1 N--; return result; } //查找t元素第一次出现的位置 public int indexOf(T t){ if(t==null){ throw new RuntimeException("查找的元素不合法"); } for (int i = 0; i < N; i++) { if (eles[i].equals(t)){ return i; } } return -1; } } //测试代码 public class SequenceListTest { public static void main(String[] args) { //创建顺序表对象 SequenceList<String> sl = new SequenceList<>(10); //测试插入 sl.insert("姚明"); sl.insert("科比"); sl.insert("麦迪"); sl.insert(1,"詹姆斯"); //测试获取 String getResult = sl.get(1); System.out.println("获取索引1处的结果为:"+getResult); //测试删除 String removeResult = sl.remove(0); System.out.println("删除的元素是:"+removeResult); //测试清空 sl.clear(); System.out.println("清空后的线性表中的元素个数为:"+sl.length()); } }
1.1.2 顺序表的遍历
import java.util.Iterator; public class SequenceList<T> implements Iterable<T>{ //存储元素的数组 private T[] eles; //记录当前顺序表中的元素个数 private int N; //构造方法 public SequenceList(int capacity){ eles = (T[])new Object[capacity]; N=0; } //将一个线性表置为空表 public void clear(){ N=0; } //判断当前线性表是否为空表 public boolean isEmpty(){ return N==0; } //获取线性表的长度 public int length(){ return N; } //获取指定位置的元素 public T get(int i){ if (i<0 || i>=N){ throw new RuntimeException("当前元素不存在!"); } return eles[i]; } //向线型表中添加元素t public void insert(T t){ if (N==eles.length){ throw new RuntimeException("当前表已满"); } eles[N++] = t; } //在i元素处插入元素t public void insert(int i,T t){ if (i==eles.length){ throw new RuntimeException("当前表已满"); } if (i<0 || i>N){ throw new RuntimeException("插入的位置不合法"); } //把i位置空出来,i位置及其后面的元素依次向后移动一位 for (int index=N;index>i;index--){ eles[index]=eles[index-1]; } //把t放到i位置处 eles[i]=t; //元素数量+1 N++; } //删除指定位置i处的元素,并返回该元素 public T remove(int i){ if (i<0 || i>N-1){ throw new RuntimeException("当前要删除的元素不存在"); } //记录i位置处的元素 T result = eles[i]; //把i位置后面的元素都向前移动一位 for (int index=i;index<N-1;index++){ eles[index]=eles[index+1]; } //当前元素数量-1 N--; return result; } //查找t元素第一次出现的位置 public int indexOf(T t){ if(t==null){ throw new RuntimeException("查找的元素不合法"); } for (int i = 0; i < N; i++) { if (eles[i].equals(t)){ return i; } } return -1; } //打印当前线性表的元素 public void showEles(){ for (int i = 0; i < N; i++) { System.out.print(eles[i]+" "); } System.out.println(); } @Override public Iterator iterator() { return new SIterator(); } private class SIterator implements Iterator{ private int cur; public SIterator(){ this.cur=0; } @Override public boolean hasNext() { return cur<N; } @Override public T next() { return eles[cur++]; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { SequenceList<String> squence = new SequenceList<>(5); //测试遍历 squence.insert(0, "姚明"); squence.insert(1, "科比"); squence.insert(2, "麦迪"); squence.insert(3, "艾佛森"); squence.insert(4, "卡特"); for (String s : squence) { System.out.println(s); } } }
1.1.3 顺序表的容量可变
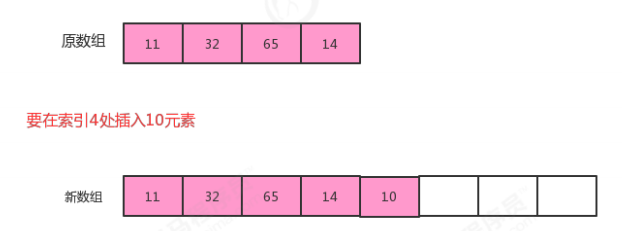

//顺序表代码 public class SequenceList<T> implements Iterable<T>{ //存储元素的数组 private T[] eles; //记录当前顺序表中的元素个数 private int N; //构造方法 public SequenceList(int capacity){ eles = (T[])new Object[capacity]; N=0; } //将一个线性表置为空表 public void clear(){ N=0; } //判断当前线性表是否为空表 public boolean isEmpty(){ return N==0; } //获取线性表的长度 public int length(){ return N; } //获取指定位置的元素 public T get(int i){ if (i<0 || i>=N){ throw new RuntimeException("当前元素不存在!"); } return eles[i]; } //向线型表中添加元素t public void insert(T t){ if (N==eles.length){ resize(eles.length*2); } eles[N++] = t; } //在i元素处插入元素t public void insert(int i,T t){ if (i<0 || i>N){ throw new RuntimeException("插入的位置不合法"); } //元素已经放满了数组,需要扩容 if (N==eles.length){ resize(eles.length*2); } //把i位置空出来,i位置及其后面的元素依次向后移动一位 for (int index=N-1;index>i;index--){ eles[index]=eles[index-1]; } //把t放到i位置处 eles[i]=t; //元素数量+1 N++; } //删除指定位置i处的元素,并返回该元素 public T remove(int i){ if (i<0 || i>N-1){ throw new RuntimeException("当前要删除的元素不存在"); } //记录i位置处的元素 T result = eles[i]; //把i位置后面的元素都向前移动一位 for (int index=i;index<N-1;index++){ eles[index]=eles[index+1]; } //当前元素数量-1 N--; //当元素已经不足数组大小的1/4,则重置数组的大小 if (N>0 && N<eles.length/4){ resize(eles.length/2); } return result; } //查找t元素第一次出现的位置 public int indexOf(T t){ if(t==null){ throw new RuntimeException("查找的元素不合法"); } for (int i = 0; i < N; i++) { if (eles[i].equals(t)){ return i; } } return -1; } //打印当前线性表的元素 public void showEles(){ for (int i = 0; i < N; i++) { System.out.print(eles[i]+" "); } System.out.println(); } @Override public Iterator iterator() { return new SIterator(); } private class SIterator implements Iterator{ private int cur; public SIterator(){ this.cur=0; } @Override public boolean hasNext() { return cur<N; } @Override public T next() { return eles[cur++]; } } //改变容量 private void resize(int newSize){ //记录旧数组 T[] temp = eles; //创建新数组 eles = (T[]) new Object[newSize]; //把旧数组中的元素拷贝到新数组 for (int i = 0; i < N; i++) { eles[i] = temp[i]; } } public int capacity(){ return eles.length; } } //测试代码 public class Test { public static void main(String[] args) throws Exception { SequenceList<String> squence = new SequenceList<>(5); //测试遍历 squence.insert(0, "姚明"); squence.insert(1, "科比"); squence.insert(2, "麦迪"); squence.insert(3, "艾佛森"); squence.insert(4, "卡特"); System.out.println(squence.capacity()); squence.insert(5,"aa"); System.out.println(squence.capacity()); squence.insert(5,"aa"); squence.insert(5,"aa"); squence.insert(5,"aa"); squence.insert(5,"aa"); squence.insert(5,"aa"); System.out.println(squence.capacity()); squence.remove(1); squence.remove(1); squence.remove(1); squence.remove(1); squence.remove(1); squence.remove(1); squence.remove(1); System.out.println(squence.capacity()); } }
1.1.4 顺序表的时间复杂度
1.1.5 java中ArrayList实现
1.2 链表

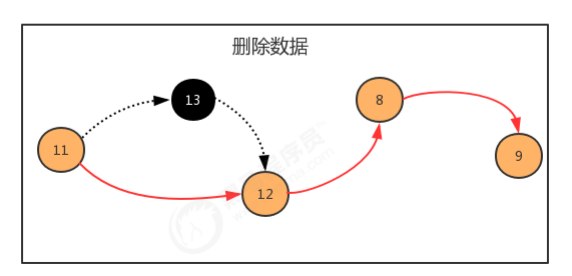

public class Node<T> { //存储元素 public T item; //指向下一个结点 public Node next; public Node(T item, Node next) { this.item = item; this.next = next; } }
public static void main(String[] args) throws Exception { //构建结点 Node<Integer> first = new Node<Integer>(11, null); Node<Integer> second = new Node<Integer>(13, null); Node<Integer> third = new Node<Integer>(12, null); Node<Integer> fourth = new Node<Integer>(8, null); Node<Integer> fifth = new Node<Integer>(9, null); //生成链表 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; }
1.2.1 单向链表

1.2.1.1 单向链表API设计

import java.util.Iterator; public class LinkList<T> implements Iterable<T> { //记录头结点 private Node head; //记录链表的长度 private int N; public LinkList(){ //初始化头结点 head = new Node(null,null); N=0; } //清空链表 public void clear(){ head.next=null; head.item=null; N=0; } //获取链表的长度 public int length(){ return N; } //判断链表是否为空 public boolean isEmpty(){ return N==0; } //获取指定位置i出的元素 public T get(int i){ if (i<0||i>=N){ throw new RuntimeException("位置不合法!"); } Node n = head.next; for (int index = 0; index < i; index++) { n = n.next; } return n.item; } //向链表中添加元素t public void insert(T t){ //找到最后一个节点 Node n = head; while(n.next!=null){ n = n.next; } Node newNode = new Node(t, null); n.next = newNode; //链表长度+1 N++; } //向指定位置i处,添加元素t public void insert(int i,T t){ if (i<0||i>=N){ throw new RuntimeException("位置不合法!"); } //寻找位置i之前的结点 Node pre = head; for (int index = 0; index <=i-1; index++) { pre = pre.next; } //位置i的结点 Node curr = pre.next; //构建新的结点,让新结点指向位置i的结点 Node newNode = new Node(t, curr); //让之前的结点指向新结点 pre.next = newNode; //长度+1 N++; } //删除指定位置i处的元素,并返回被删除的元素 public T remove(int i){ if (i<0 || i>=N){ throw new RuntimeException("位置不合法"); } //寻找i之前的元素 Node pre = head; for (int index = 0; index <=i-1; index++) { pre = pre.next; } //当前i位置的结点 Node curr = pre.next; //前一个结点指向下一个结点,删除当前结点 pre.next = curr.next; //长度-1 N--; return curr.item; } //查找元素t在链表中第一次出现的位置 public int indexOf(T t){ Node n = head; for (int i = 0;n.next!=null;i++){ n = n.next; if (n.item.equals(t)){ return i; } } return -1; } //结点类 private class Node{ //存储数据 T item; //下一个结点 Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } @Override public Iterator iterator() { return new LIterator(); } private class LIterator implements Iterator<T>{ private Node n; public LIterator() { this.n = head; } @Override public boolean hasNext() { return n.next!=null; } @Override public T next() { n = n.next; return n.item; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { LinkList<String> list = new LinkList<>(); list.insert(0,"张三"); list.insert(1,"李四"); list.insert(2,"王五"); list.insert(3,"赵六"); //测试length方法 for (String s : list) { System.out.println(s); } System.out.println(list.length()); System.out.println("-------------------"); //测试get方法 System.out.println(list.get(2)); System.out.println("------------------------"); //测试remove方法 String remove = list.remove(1); System.out.println(remove); System.out.println(list.length()); System.out.println("----------------");; for (String s : list) { System.out.println(s); } } }
1.2.2 双向链表

1.2.2.1 结点API设计

1.2.2.2 双向链表API设计

1.2.2.3 双向链表代码实现
import java.util.Iterator; public class TowWayLinkList<T> implements Iterable<T>{ //首结点 private Node head; //最后一个结点 private Node last; //链表的长度 private int N; public TowWayLinkList() { last = null; head = new Node(null,null,null); N=0; } //清空链表 public void clear(){ last=null; head.next=last; head.pre=null; head.item=null; N=0; } //获取链表长度 public int length(){ return N; } //判断链表是否为空 public boolean isEmpty(){ return N==0; } //插入元素t public void insert(T t){ if (last==null){ last = new Node(t,head,null); head.next = last; }else{ Node oldLast = last; Node node = new Node(t, oldLast, null); oldLast.next = node; last = node; } //长度+1 N++; } //向指定位置i处插入元素t public void insert(int i,T t){ if (i<0 || i>=N){ throw new RuntimeException("位置不合法"); } //找到位置i的前一个结点 Node pre = head; for (int index = 0; index < i; index++) { pre = pre.next; } //当前结点 Node curr = pre.next; //构建新结点 Node newNode = new Node(t, pre, curr); curr.pre= newNode; pre.next = newNode; //长度+1 N++; } //获取指定位置i处的元素 public T get(int i){ if (i<0||i>=N){ throw new RuntimeException("位置不合法"); } //寻找当前结点 Node curr = head.next; for (int index = 0; index <i; index++) { curr = curr.next; } return curr.item; } //找到元素t在链表中第一次出现的位置 public int indexOf(T t){ Node n= head; for (int i=0;n.next!=null;i++){ n = n.next; if (n.next.equals(t)){ return i; } } return -1; } //删除位置i处的元素,并返回该元素 public T remove(int i){ if (i<0 || i>=N){ throw new RuntimeException("位置不合法"); } //寻找i位置的前一个元素 Node pre = head; for (int index = 0; index <i ; index++) { pre = pre.next; } //i位置的元素 Node curr = pre.next; //i位置的下一个元素 Node curr_next = curr.next; pre.next = curr_next; curr_next.pre = pre; //长度-1; N--; return curr.item; } //获取第一个元素 public T getFirst(){ if (isEmpty()){ return null; } return head.next.item; } //获取最后一个元素 public T getLast(){ if (isEmpty()){ return null; } return last.item; } @Override public Iterator<T> iterator() { return new TIterator(); } private class TIterator implements Iterator{ private Node n = head; @Override public boolean hasNext() { return n.next!=null; } @Override public Object next() { n = n.next; return n.item; } } //结点类 private class Node{ public Node(T item, Node pre, Node next) { this.item = item; this.pre = pre; this.next = next; } //存储数据 public T item; //指向上一个结点 public Node pre; //指向下一个结点 public Node next; } } //测试代码 public class Test { public static void main(String[] args) throws Exception { TowWayLinkList<String> list = new TowWayLinkList<>(); list.insert("乔峰"); list.insert("虚竹"); list.insert("段誉"); list.insert(1,"鸠摩智"); list.insert(3,"叶二娘"); for (String str : list) { System.out.println(str); } System.out.println("----------------------"); String tow = list.get(2); System.out.println(tow); System.out.println("-------------------------"); String remove = list.remove(3); System.out.println(remove); System.out.println(list.length()); System.out.println("--------------------"); System.out.println(list.getFirst()); System.out.println(list.getLast()); } }
1.2.2.4 java中LinkedList实现
1.2.3 链表的复杂度分析
1.2.4 链表反转
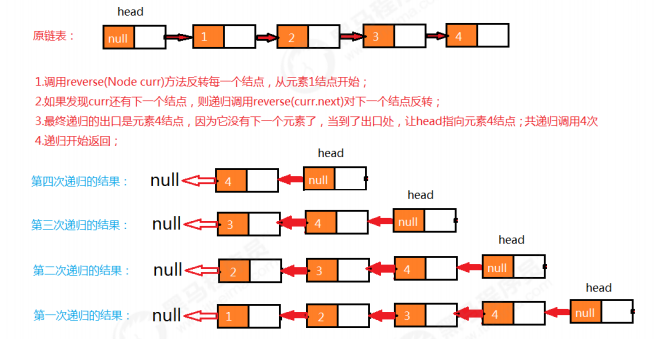
public void reverse(){ if (N==0){ //当前是空链表,不需要反转 return; } reverse(head.next); } /** * * @param curr 当前遍历的结点 * @return 反转后当前结点上一个结点 */ public Node reverse(Node curr){ //已经到了最后一个元素 if (curr.next==null){ //反转后,头结点应该指向原链表中的最后一个元素 head.next=curr; return curr; } //当前结点的上一个结点 Node pre = reverse(curr.next); pre.next = curr; //当前结点的下一个结点设为null curr.next=null; //返回当前结点 return curr; } //测试代码 public class Test { public static void main(String[] args) throws Exception { LinkList<Integer> list = new LinkList<>(); list.insert(1); list.insert(2); list.insert(3); list.insert(4); for (Integer i : list) { System.out.print(i+" "); } System.out.println(); System.out.println("--------------------"); list.reverse(); for (Integer i : list) { System.out.print(i+" "); } } }
public class Test { public static void main(String[] args) throws Exception { Node<String> first = new Node<String>("aa", null); Node<String> second = new Node<String>("bb", null); Node<String> third = new Node<String>("cc", null); Node<String> fourth = new Node<String>("dd", null); Node<String> fifth = new Node<String>("ee", null); Node<String> six = new Node<String>("ff", null); Node<String> seven = new Node<String>("gg", null); //完成结点之间的指向 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; fifth.next = six; six.next = seven; //查找中间值 String mid = getMid(first); System.out.println("中间值为:"+mid); } /** * @param first 链表的首结点 * @return 链表的中间结点的值 */ public static String getMid(Node<String> first) { return null; } //结点类 private static class Node<T> { //存储数据 T item; //下一个结点 Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } }

/** * @param first 链表的首结点 * @return 链表的中间结点的值 */ public static String getMid(Node<String> first) { Node<String> slow = first; Node<String> fast = first; while(fast!=null && fast.next!=null){ fast=fast.next.next; slow=slow.next; } return slow.item; }
1.2.5.2 单向链表是否有环问题
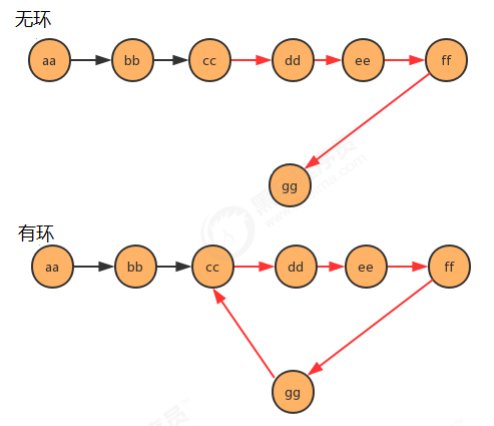
public class Test { public static void main(String[] args) throws Exception { Node<String> first = new Node<String>("aa", null); Node<String> second = new Node<String>("bb", null); Node<String> third = new Node<String>("cc", null); Node<String> fourth = new Node<String>("dd", null); Node<String> fifth = new Node<String>("ee", null); Node<String> six = new Node<String>("ff", null); Node<String> seven = new Node<String>("gg", null); //完成结点之间的指向 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; fifth.next = six; six.next = seven; //产生环 seven.next = third; //判断链表是否有环 boolean circle = isCircle(first); System.out.println("first链表中是否有环:"+circle); } /** * 判断链表中是否有环 * @param first 链表首结点 * @return ture为有环,false为无环 */ public static boolean isCircle(Node<String> first) { return false; } //结点类 private static class Node<T> { //存储数据 T item; //下一个结点 Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } }
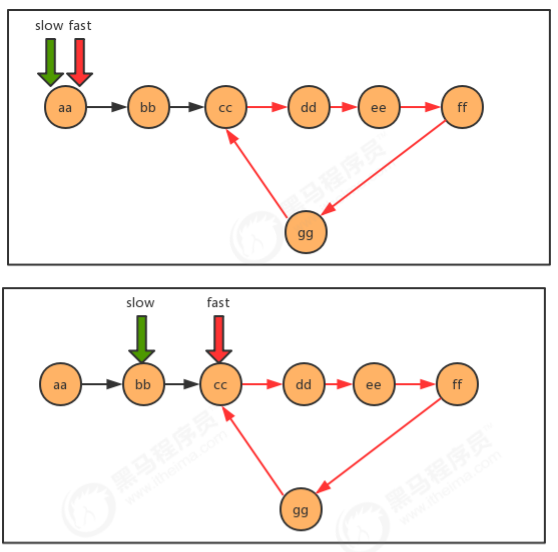
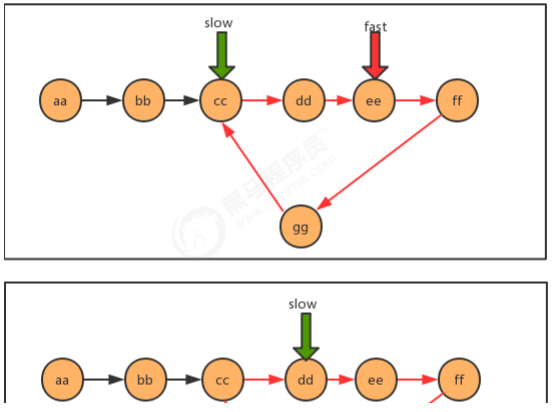

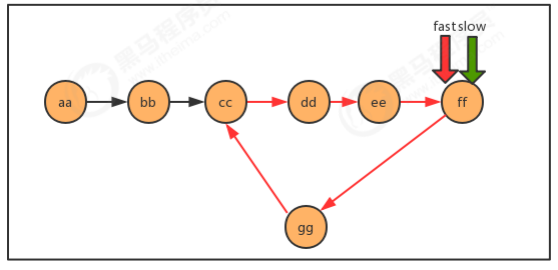
代码:
/** * 判断链表中是否有环 * @param first 链表首结点 * @return ture为有环,false为无环 */ public static boolean isCircle(Node<String> first) { Node<String> slow = first; Node<String> fast = first; while(fast!=null && fast.next!=null){ fast = fast.next.next; slow = slow.next; if (fast.equals(slow)){ return true; } } return false; }
1.2.5.3 有环链表入口问题
public class Test { public static void main(String[] args) throws Exception { Node<String> first = new Node<String>("aa", null); Node<String> second = new Node<String>("bb", null); Node<String> third = new Node<String>("cc", null); Node<String> fourth = new Node<String>("dd", null); Node<String> fifth = new Node<String>("ee", null); Node<String> six = new Node<String>("ff", null); Node<String> seven = new Node<String>("gg", null); //完成结点之间的指向 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; fifth.next = six; six.next = seven; //产生环 seven.next = third; //查找环的入口结点 Node<String> entrance = getEntrance(first); System.out.println("first链表中环的入口结点元素为:"+entrance.item); } /** * 查找有环链表中环的入口结点 * @param first 链表首结点 * @return 环的入口结点 */ public static Node getEntrance(Node<String> first) { return null; } //结点类 private static class Node<T> { //存储数据 T item; //下一个结点 Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } }


代码: /** * 查找有环链表中环的入口结点 * @param first 链表首结点 * @return 环的入口结点 */ public static Node getEntrance(Node<String> first) { Node<String> slow = first; Node<String> fast = first; Node<String> temp = null; while(fast!=null && fast.next!=null){ fast = fast.next.next; slow=slow.next; if (fast.equals(slow)){ temp = first; continue; } if (temp!=null){ temp=temp.next; if (temp.equals(slow)){ return temp; } } } return null; }
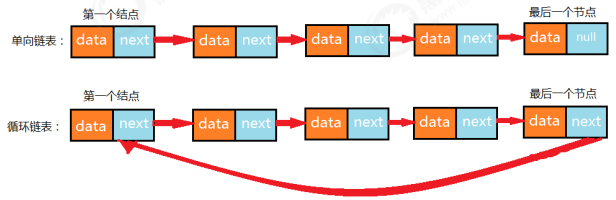
public class Test { public static void main(String[] args) throws Exception { //构建结点 Node<Integer> first = new Node<Integer>(1, null); Node<Integer> second = new Node<Integer>(2, null); Node<Integer> third = new Node<Integer>(3, null); Node<Integer> fourth = new Node<Integer>(4, null); Node<Integer> fifth = new Node<Integer>(5, null); Node<Integer> six = new Node<Integer>(6, null); Node<Integer> seven = new Node<Integer>(7, null); //构建单链表 first.next = second; second.next = third; third.next = fourth; fourth.next = fifth; fifth.next = six; six.next = seven; //构建循环链表,让最后一个结点指向第一个结点 seven.next = first; } }
1.2.7 约瑟夫问题

public class Test { public static void main(String[] args) throws Exception { //1.构建循环链表 Node<Integer> first = null; //记录前一个结点 Node<Integer> pre = null; for (int i = 1; i <= 41; i++) { //第一个元素 if (i==1){ first = new Node(i,null); pre = first; continue; } Node<Integer> node = new Node<>(i,null); pre.next = node; pre = node; if (i==41){ //构建循环链表,让最后一个结点指向第一个结点 pre.next=first; } } //2.使用count,记录当前的报数值 int count=0; //3.遍历链表,每循环一次,count++ Node<Integer> n = first; Node<Integer> before = null; while(n!=n.next){ //4.判断count的值,如果是3,则从链表中删除这个结点并打印结点的值,把count重置为0; count++; if (count==3){ //删除当前结点 before.next = n.next; System.out.print(n.item+","); count=0; n = n.next; }else{ before=n; n = n.next; } } /*打印剩余的最后那个人*/ System.out.println(n.item); } }
1.3 栈
1.3.1 栈概述
1.3.1.1 生活中的栈

1.3.1.2 计算机中的栈

1.3.2 栈的实现
1.3.2.1 栈API设计

1.3.2.2 栈代码实现
此处首节点是栈顶元素。创建一个node,node的item为null,next也为null.一直往下插入节点。这个node 一直为head。就是它的item为null,next指向下一个节点,所有节点都往node下面插入。
//栈代码 import java.util.Iterator; public class Stack<T> implements Iterable<T>{ //记录首结点 private Node head; //栈中元素的个数 private int N; public Stack() { head = new Node(null,null); N=0; } //判断当前栈中元素个数是否为0 public boolean isEmpty(){ return N==0; } //把t元素压入栈 public void push(T t){ Node oldNext = head.next; Node node = new Node(t, oldNext); head.next = node; //个数+1 N++; } //弹出栈顶元素 public T pop(){ Node oldNext = head.next; if (oldNext==null){ return null; } //删除首个元素 head.next = head.next.next; //个数-1 N--; return oldNext.item; } //获取栈中元素的个数 public int size(){ return N; } @Override public Iterator<T> iterator() { return new SIterator(); } private class SIterator implements Iterator<T>{ private Node n = head; @Override public boolean hasNext() { return n.next!=null; } @Override public T next() { Node node = n.next; n = n.next; return node.item; } } private class Node{ public T item; public Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { Stack<String> stack = new Stack<>(); stack.push("a"); stack.push("b"); stack.push("c"); stack.push("d"); for (String str : stack) { System.out.print(str+" "); } System.out.println("-----------------------------"); String result = stack.pop(); System.out.println("弹出了元素:"+result); System.out.println(stack.size()); } }
1.3.3 案例
1.3.3.1 括号匹配问题
public class BracketsMatch { public static void main(String[] args) { String str = "(上海(长安)())"; boolean match = isMatch(str); System.out.println(str+"中的括号是否匹配:"+match); } /** * 判断str中的括号是否匹配 * @param str 括号组成的字符串 * @return 如果匹配,返回true,如果不匹配,返回false */ public static boolean isMatch(String str){ return false; } }


public class BracketsMatch { public static void main(String[] args) { String str = "(fdafds(fafds)())"; boolean match = isMatch(str); System.out.println(str + "中的括号是否匹配:" + match); } /** * 判断str中的括号是否匹配 * * @param str 括号组成的字符串 * @return 如果匹配,返回true,如果不匹配,返回false */ public static boolean isMatch(String str) { //1.创建一个栈用来存储左括号 Stack<String> chars = new Stack<>(); //2.从左往右遍历字符串,拿到每一个字符 for (int i = 0; i < str.length(); i++) { String currChar = str.charAt(i) + ""; //3.判断该字符是不是左括号,如果是,放入栈中存储 if (currChar.equals("(")) { chars.push(currChar); } else if (currChar.equals(")")) {//4.判断该字符是不是右括号,如果不是,继续下一次循 环 //5.如果该字符是右括号,则从栈中弹出一个元素t; String t = chars.pop(); //6.判断元素t是否为null,如果不是,则证明有对应的左括号,如果不是,则证明没有对应的 左括号 if (t == null) { return false; } } } //7.循环结束后,判断栈中还有没有剩余的左括号,如果有,则不匹配,如果没有,则匹配 if (chars.size() == 0) { return true; } else { return false; } } }
1.3.3.2 逆波兰表达式求值问题

给定一个只包含加减乘除四种运算的逆波兰表达式的数组表示方式,求出该逆波兰表达式的结果。 public class ReversePolishNotation { public static void main(String[] args) { //中缀表达式3*(17-15)+18/6的逆波兰表达式如下 String[] notation = {"3", "17", "15", "-", "*","18", "6","/","+"}; int result = caculate(notation); System.out.println("逆波兰表达式的结果为:"+result); } /** * @param notaion 逆波兰表达式的数组表示方式 * @return 逆波兰表达式的计算结果 */ public static int caculate(String[] notaion){ return -1; } }
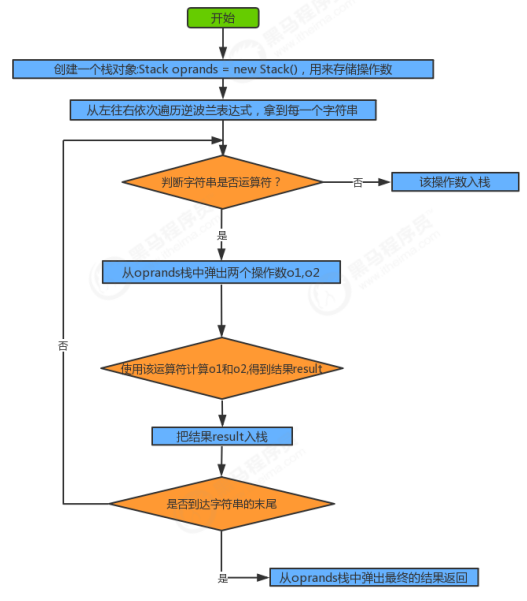
public class ReversePolishNotation { public static void main(String[] args) { //中缀表达式3*(17-15)+18/6的逆波兰表达式如下 String[] notation = {"3", "17", "15", "-", "*", "18", "6", "/", "+"}; int result = caculate(notation); System.out.println("逆波兰表达式的结果为:" + result); } /** * @param notaion 逆波兰表达式的数组表示方式 * @return 逆波兰表达式的计算结果 */ public static int caculate(String[] notaion) { //1.创建一个栈对象oprands存储操作数 Stack<Integer> oprands = new Stack<>(); //2.从左往右遍历逆波兰表达式,得到每一个字符串 for (int i = 0; i < notaion.length; i++) { String curr = notaion[i]; //3.判断该字符串是不是运算符,如果不是,把该该操作数压入oprands栈中 Integer o1; Integer o2; Integer result; switch (curr) { case "+": //4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2 o1 = oprands.pop(); o2 = oprands.pop(); //5.使用该运算符计算o1和o2,得到结果result result = o2 + o1; //6.把该结果压入oprands栈中 oprands.push(result); break; case "-": //4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2 o1 = oprands.pop(); o2 = oprands.pop(); //5.使用该运算符计算o1和o2,得到结果result result = o2 - o1; //6.把该结果压入oprands栈中 oprands.push(result); break; case "*": //4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2 o1 = oprands.pop(); o2 = oprands.pop(); //5.使用该运算符计算o1和o2,得到结果result result = o2 * o1; //6.把该结果压入oprands栈中 oprands.push(result); break; case "/": //4.如果是运算符,则从oprands栈中弹出两个操作数o1,o2 o1 = oprands.pop(); o2 = oprands.pop(); //5.使用该运算符计算o1和o2,得到结果result result = o2 / o1; //6.把该结果压入oprands栈中 oprands.push(result); break; default: oprands.push(Integer.parseInt(curr)); break; } } //7.遍历结束后,拿出栈中最终的结果返回 Integer result = oprands.pop(); return result; } }
1.4 队列
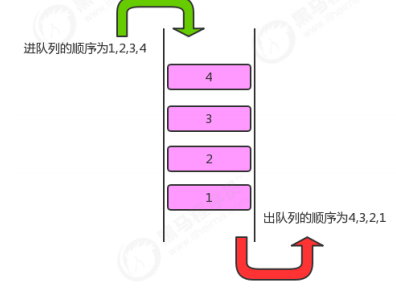

1.4.1 队列的API设计
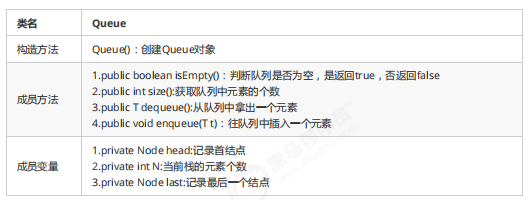
1.4.2 队列的实现
//队列代码 import java.util.Iterator; public class Queue<T> implements Iterable<T>{ //记录首结点 private Node head; //记录最后一个结点 private Node last; //记录队列中元素的个数 private int N; public Queue() { head = new Node(null,null); last=null; N=0; } //判断队列是否为空 public boolean isEmpty(){ return N==0; } //返回队列中元素的个数 public int size(){ return N; } //向队列中插入元素t public void enqueue(T t){ if (last==null){ last = new Node(t,null); head.next=last; }else{ Node oldLast = last; last = new Node(t,null); oldLast.next=last; } //个数+1 N++; } //从队列中拿出一个元素 public T dequeue(){ if (isEmpty()){ return null; } Node oldFirst = head.next; head.next = oldFirst.next; N--; if (isEmpty()){ last=null; } return oldFirst.item; } @Override public Iterator<T> iterator() { return new QIterator(); } private class QIterator implements Iterator<T>{ private Node n = head; @Override public boolean hasNext() { return n.next!=null; } @Override public T next() { Node node = n.next; n = n.next; return node.item; } } private class Node{ public T item; public Node next; public Node(T item, Node next) { this.item = item; this.next = next; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { Queue<String> queue = new Queue<>(); queue.enqueue("a"); queue.enqueue("b"); queue.enqueue("c"); queue.enqueue("d"); for (String str : queue) { System.out.print(str+" "); } System.out.println("-----------------------------"); String result = queue.dequeue(); System.out.println("出列了元素:"+result); System.out.println(queue.size()); } }
一、符号表
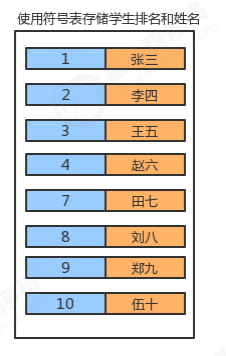

1.1 符号表API设计


1.2 符号表实现
//符号表 public class SymbolTable<Key,Value> { //记录首结点 private Node head; //记录符号表中元素的个数 private int N; public SymbolTable() { head = new Node(null,null,null); N=0; } //获取符号表中键值对的个数 public int size(){ return N; } //往符号表中插入键值对 public void put(Key key,Value value){ //先从符号表中查找键为key的键值对 Node n = head; while(n.next!=null){ n = n.next; if (n.key.equals(key)){ n.value=value; return; } } //符号表中没有键为key的键值对 Node oldFirst = head.next; Node newFirst = new Node(key,value,oldFirst); head.next = newFirst; //个数+1 N++; } //删除符号表中键为key的键值对 public void delete(Key key){ Node n = head; while(n.next!=null){ if (n.next.key.equals(key)){ n.next = n.next.next; N--; return; } n = n.next; } } //从符号表中获取key对应的值 public Value get(Key key){ Node n = head; while(n.next!=null){ n = n.next; if (n.key.equals(key)){ return n.value; } } return null; } private class Node{ //键 public Key key; //值 public Value value; //下一个结点 public Node next; public Node(Key key, Value value, Node next) { this.key = key; this.value = value; this.next = next; } } } //测试类 public class Test { public static void main(String[] args) throws Exception { SymbolTable<Integer, String> st = new SymbolTable<>(); st.put(1, "张三"); st.put(3, "李四"); st.put(5, "王五"); System.out.println(st.size()); st.put(1,"老三"); System.out.println(st.get(1)); System.out.println(st.size()); st.delete(1); System.out.println(st.size()); } }
1.3 有序符号表
//有序符号表 public class OrderSymbolTable<Key extends Comparable<Key>,Value> { //记录首结点 private Node head; //记录符号表中元素的个数 private int N; public OrderSymbolTable() { head = new Node(null,null,null); N=0; } //获取符号表中键值对的个数 public int size(){ return N; } //往符号表中插入键值对 public void put(Key key,Value value){ //记录当前结点 Node curr = head.next; //记录上一个结点 Node pre = head; //1.如果key大于当前结点的key,则一直寻找下一个结点 while(curr!=null && key.compareTo(curr.key)>0){ pre = curr; curr = curr.next; } //2.如果当前结点curr的key和将要插入的key一样,则替换 if (curr!=null && curr.key.compareTo(key)==0){ curr.value=value; return; } //3.没有找到相同的key,把新结点插入到curr之前 Node newNode = new Node(key, value, curr); pre.next = newNode; } //删除符号表中键为key的键值对 public void delete(Key key){ Node n = head; while(n.next!=null){ if (n.next.key.equals(key)){ n.next = n.next.next; N--; return; } n = n.next; } } //从符号表中获取key对应的值 public Value get(Key key){ Node n = head; while(n.next!=null){ n = n.next; if (n.key.equals(key)){ return n.value; } } return null; } private class Node{ //键 public Key key; //值 public Value value; //下一个结点 public Node next; public Node(Key key, Value value, Node next) { this.key = key; this.value = value; this.next = next; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { OrderSymbolTable<Integer, String> bt = new OrderSymbolTable<>(); bt.put(4, "二哈"); bt.put(3, "张三"); bt.put(1, "李四"); bt.put(1, "aa"); bt.put(5, "王五"); } }
一、二叉树入门
1.1树的基本定义

1.2 树的相关术语
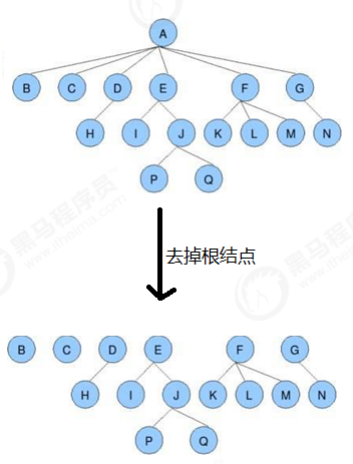
1.3 二叉树的基本定义
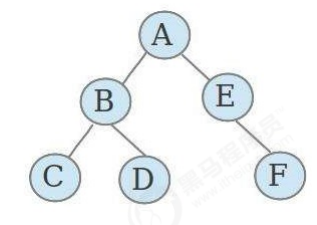
满二叉树:
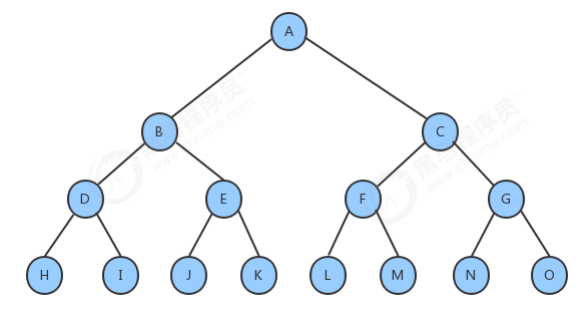
完全二叉树:

1.4 二叉查找树的创建
1.4.1二叉树的结点类
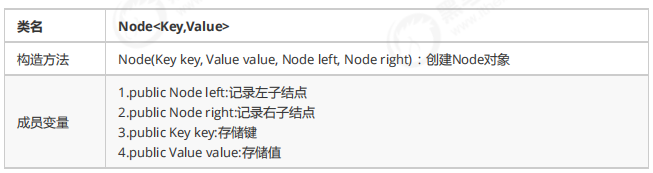
private class Node<Key,Value>{ //存储键 public Key key; //存储值 private Value value; //记录左子结点 public Node left; //记录右子结点 public Node right; public Node(Key key, Value value, Node left, Node right) { this.key = key; this.value = value; this.left = left; this.right = right; } }
1.4.2 二叉查找树API设计

1.4.3 二叉查找树实现

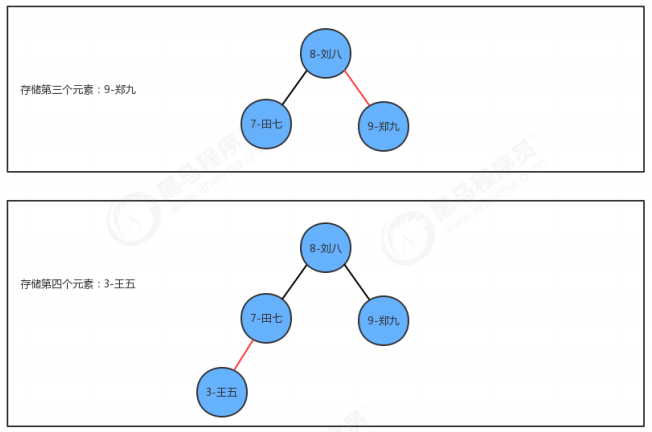
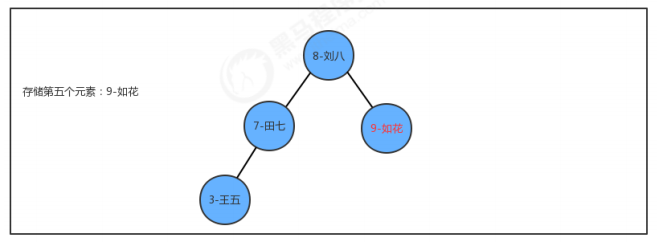
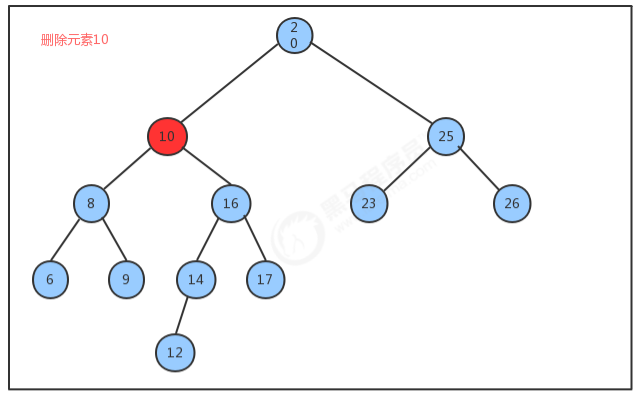



//二叉树代码 public class BinaryTree<Key extends Comparable<Key>, Value> { //记录根结点 private Node root; //记录树中元素的个数 private int N; //获取树中元素的个数 public int size() { return N; } //向树中添加元素key-value public void put(Key key, Value value) { root = put(root, key, value); } //向指定的树x中添加key-value,并返回添加元素后新的树 private Node put(Node x, Key key, Value value) { if (x == null) { //个数+1 N++; return new Node(key, value, null, null); } int cmp = key.compareTo(x.key); if (cmp > 0) { //新结点的key大于当前结点的key,继续找当前结点的右子结点 x.right = put(x.right, key, value); } else if (cmp < 0) { //新结点的key小于当前结点的key,继续找当前结点的左子结点 x.left = put(x.left, key, value); } else { //新结点的key等于当前结点的key,把当前结点的value进行替换 x.value = value; } return x; } //查询树中指定key对应的value public Value get(Key key) { return get(root, key); } //从指定的树x中,查找key对应的值 public Value get(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp > 0) { //如果要查询的key大于当前结点的key,则继续找当前结点的右子结点; return get(x.right, key); } else if (cmp < 0) { //如果要查询的key小于当前结点的key,则继续找当前结点的左子结点; return get(x.left, key); } else { //如果要查询的key等于当前结点的key,则树中返回当前结点的value。 return x.value; } } //删除树中key对应的value public void delete(Key key) { root = delete(root, key); } //删除指定树x中的key对应的value,并返回删除后的新树 public Node delete(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp > 0) { //新结点的key大于当前结点的key,继续找当前结点的右子结点 x.right = delete(x.right, key); } else if (cmp < 0) { //新结点的key小于当前结点的key,继续找当前结点的左子结点 x.left = delete(x.left, key); } else { //新结点的key等于当前结点的key,当前x就是要删除的结点 //1.如果当前结点的右子树不存在,则直接返回当前结点的左子结点 if (x.right == null) { return x.left; } //2.如果当前结点的左子树不存在,则直接返回当前结点的右子结点 if (x.left == null) { return x.right; } //3.当前结点的左右子树都存在 //3.1找到右子树中最小的结点 Node minNode = x.right; while (minNode.left != null) { minNode = minNode.left; } //3.2删除右子树中最小的结点 Node n = x.right; while (n.left != null) { if (n.left.left == null) { n.left = null; } else { n = n.left; } } //3.3让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点 minNode的右子树 minNode.left = x.left; minNode.right = x.right; //3.4让被删除结点的父节点指向最小结点minNode x = minNode; //个数-1 N--; } return x; } private class Node { //存储键 public Key key; //存储值 private Value value; //记录左子结点 public Node left; //记录右子结点 public Node right; public Node(Key key, Value value, Node left, Node right) { this.key = key; this.value = value; this.left = left; this.right = right; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { BinaryTree<Integer, String> bt = new BinaryTree<>(); bt.put(4, "二哈"); bt.put(1, "张三"); bt.put(3, "李四"); bt.put(5, "王五"); System.out.println(bt.size()); bt.put(1,"老三"); System.out.println(bt.get(1)); System.out.println(bt.size()); bt.delete(1); System.out.println(bt.size()); } }
1.4.4 二叉查找树其他便捷方法
1.4.4.1 查找二叉树中最小的键

//找出整个树中最小的键 public Key min(){ return min(root).key; } //找出指定树x中最小的键所在的结点 private Node min(Node x){ if (x.left!=null){ return min(x.left); }else{ return x; } }
1.4.4.2 查找二叉树中最大的键

1.5 二叉树的基础遍历
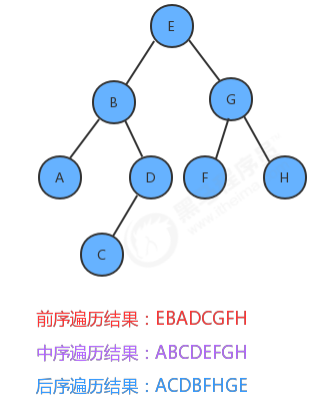
1.5.1 前序遍历
//使用前序遍历,获取整个树中的所有键 public Queue<Key> preErgodic(){ Queue<Key> keys = new Queue<>(); preErgodic(root,keys); return keys; } //使用前序遍历,把指定树x中的所有键放入到keys队列中 private void preErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } //1.把当前结点的key放入到队列中; keys.enqueue(x.key); //2.找到当前结点的左子树,如果不为空,递归遍历左子树 if (x.left!=null){ preErgodic(x.left,keys); } //3.找到当前结点的右子树,如果不为空,递归遍历右子树 if (x.right!=null){ preErgodic(x.right,keys); } } //测试代码 public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.preErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } } }
1.5.2 中序遍历
public Queue<Key> midErgodic(){ Queue<Key> keys = new Queue<>(); midErgodic(root,keys); } //使用中序遍历,把指定树x中的所有键放入到keys队列中 private void midErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } //1.找到当前结点的左子树,如果不为空,递归遍历左子树 if (x.left!=null){ midErgodic(x.left,keys); } //2.把当前结点的key放入到队列中; keys.enqueue(x.key); //3.找到当前结点的右子树,如果不为空,递归遍历右子树 if (x.right!=null){ midErgodic(x.right,keys); } } //测试代码 public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.midErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } } }
1.5.3 后序遍历
//使用后序遍历,获取整个树中的所有键 public Queue<Key> afterErgodic(){ Queue<Key> keys = new Queue<>(); afterErgodic(root,keys); return keys; } //使用后序遍历,把指定树x中的所有键放入到keys队列中 private void afterErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } //1.找到当前结点的左子树,如果不为空,递归遍历左子树 if (x.left!=null){ afterErgodic(x.left,keys); } //2.找到当前结点的右子树,如果不为空,递归遍历右子树 if (x.right!=null){ afterErgodic(x.right,keys); } //3.把当前结点的key放入到队列中; keys.enqueue(x.key); } //测试代码 public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.afterErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } } }
1.6 二叉树的层序遍历
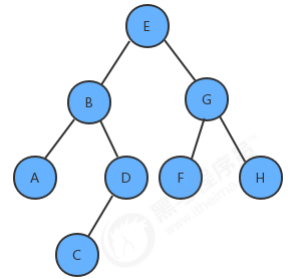
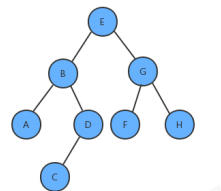
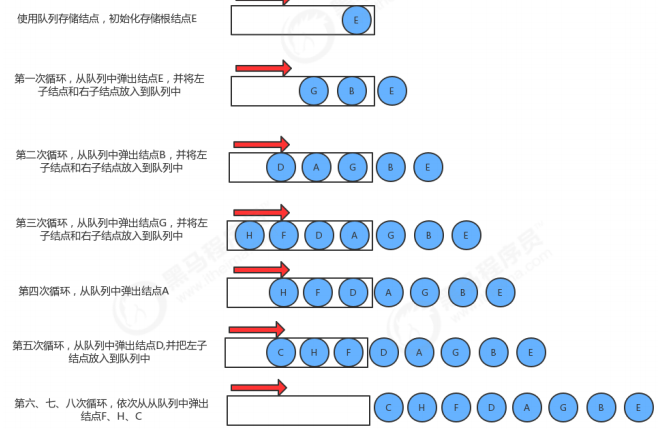
//使用层序遍历得到树中所有的键 public Queue<Key> layerErgodic(){ Queue<Key> keys = new Queue<>(); Queue<Node> nodes = new Queue<>(); nodes.enqueue(root); while(!nodes.isEmpty()){ Node x = nodes.dequeue(); keys.enqueue(x.key); if (x.left!=null){ nodes.enqueue(x.left); } if (x.right!=null){ nodes.enqueue(x.right); } } return keys; } //测试代码 public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); Queue<String> queue = bt.layerErgodic(); for (String key : queue) { System.out.println(key+"="+bt.get(key)); } } }
1.7 二叉树的最大深度问题
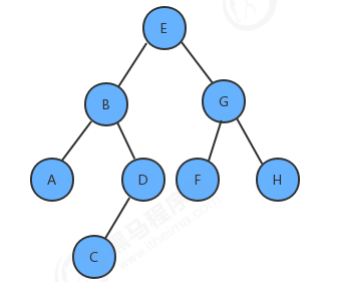
//计算整个树的最大深度 public int maxDepth() { return maxDepth(root); } //计算指定树x的最大深度 private int maxDepth(Node x) { //1.如果根结点为空,则最大深度为0; if (x == null) { return 0; } int max = 0; int maxL = 0; int maxR = 0; //2.计算左子树的最大深度; if (x.left != null) { maxL = maxDepth(x.left); } //3.计算右子树的最大深度; if (x.right != null) { maxR = maxDepth(x.right); } //4.当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1 max = maxL > maxR ? maxL + 1 : maxR + 1; return max; } //测试代码 public class Test { public static void main(String[] args) throws Exception { BinaryTree<String, String> bt = new BinaryTree<>(); bt.put("E", "5"); bt.put("B", "2"); bt.put("G", "7"); bt.put("A", "1"); bt.put("D", "4"); bt.put("F", "6"); bt.put("H", "8"); bt.put("C", "3"); int i = bt.maxDepth(); System.out.println(i); } }
1.8 折纸问题
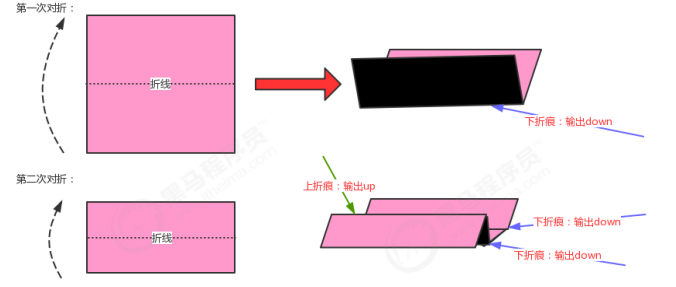

public class PaperFolding { public static void main(String[] args) { //构建折痕树 Node tree = createTree(3); //遍历折痕树,并打印 printTree(tree); } //3.使用中序遍历,打印出树中所有结点的内容; private static void printTree(Node tree) { if (tree==null){ return; } printTree(tree.left); System.out.print(tree.item+","); printTree(tree.right); } //2.构建深度为N的折痕树; private static Node createTree(int N) { Node root = null; for (int i = 0; i <N ; i++) { if (i==0){ //1.第一次对折,只有一条折痕,创建根结点; root = new Node("down",null,null); }else{ //2.如果不是第一次对折,则使用队列保存根结点; Queue<Node> queue = new Queue<>(); queue.enqueue(root); //3.循环遍历队列: while(!queue.isEmpty()){ //3.1从队列中拿出一个结点; Node tmp = queue.dequeue(); //3.2如果这个结点的左子结点不为空,则把这个左子结点添加到队列中; if (tmp.left!=null){ queue.enqueue(tmp.left); } //3.3如果这个结点的右子结点不为空,则把这个右子结点添加到队列中; if (tmp.right!=null){ queue.enqueue(tmp.right); } //3.4判断当前结点的左子结点和右子结点都不为空,如果是,则需要为当前结点创建一个 值为down的左子结点,一个值为up的右子结点。 if (tmp.left==null && tmp.right==null){ tmp.left = new Node("down",null,null); tmp.right = new Node("up",null,null); } } } } return root; } //1.定义结点类 private static class Node{ //存储结点元素 String item; //左子结点 Node left; //右子结点 Node right; public Node(String item, Node left, Node right) { this.item = item; this.left = left; this.right = right; } } }
一、堆
1.1 堆的定义
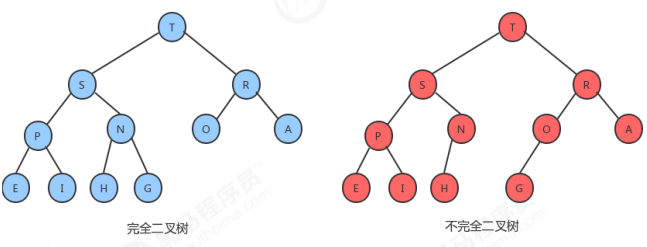
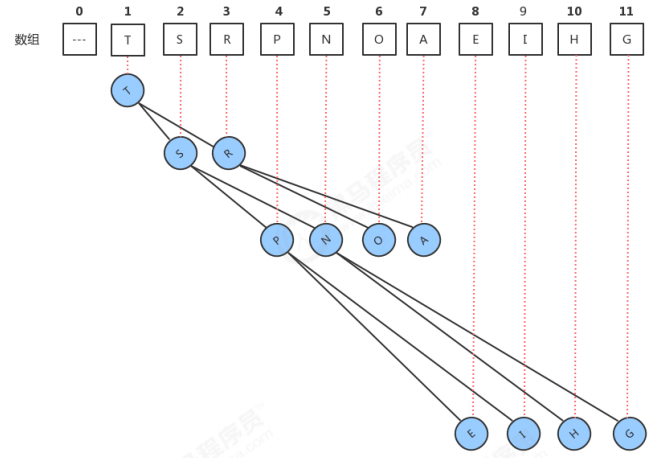
1.2 堆的API设计
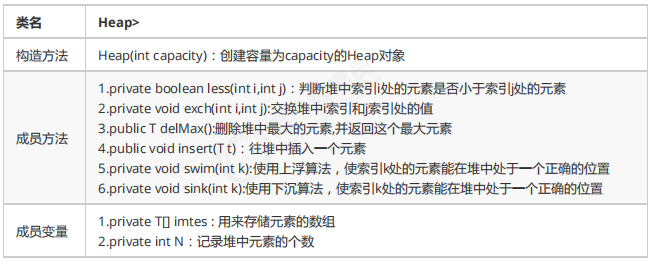
1.3 堆的实现
1.4.1 insert插入方法的实现
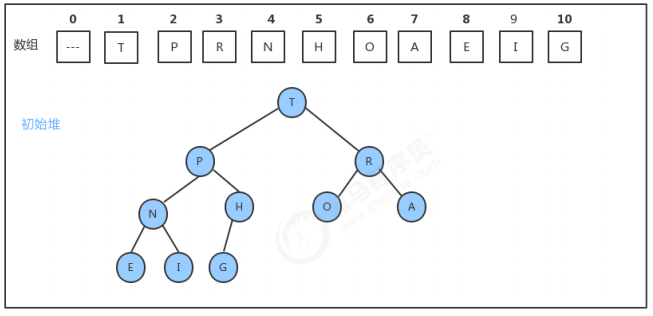
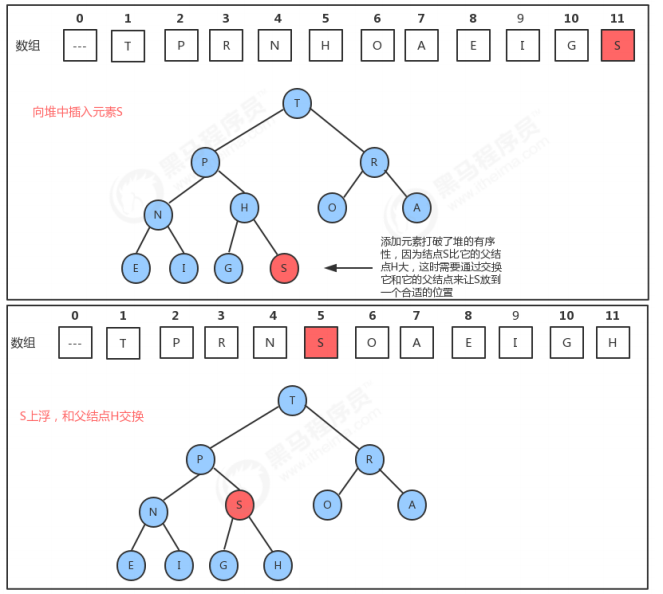

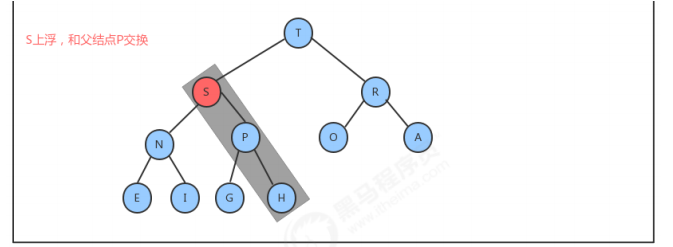
1.4.2 delMax删除最大元素方法的实现

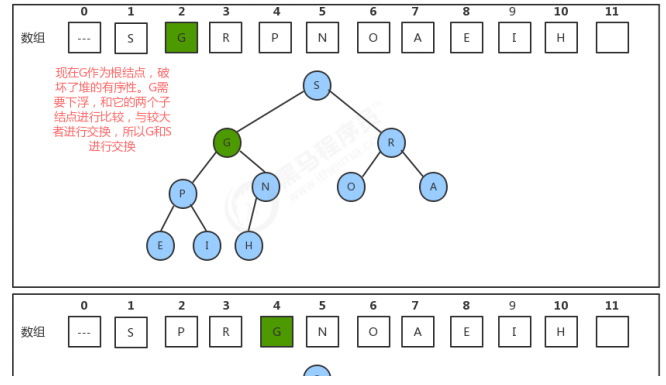
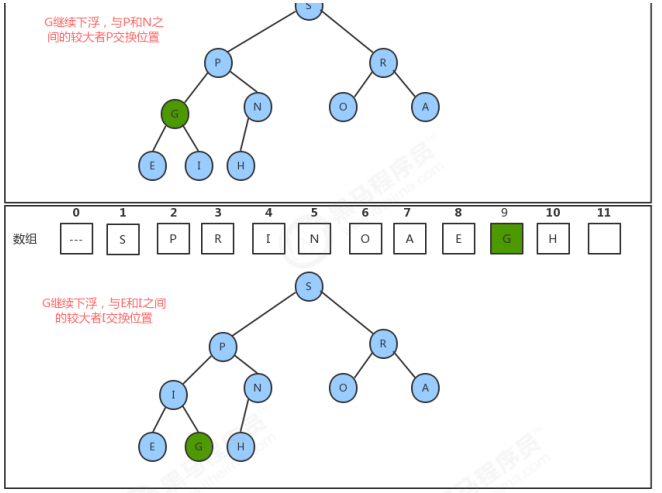
1.4.3 堆的实现代码
//堆代码 public class Heap<T extends Comparable<T>> { //存储堆中的元素 private T[] items; //记录堆中元素的个数 private int N; public Heap(int capacity) { items = (T[]) new Comparable[capacity+1]; N=0; } //判断堆中索引i处的元素是否小于索引j处的元素 private boolean less(int i,int j){ return items[i].compareTo(items[j])<0; } //交换堆中i索引和j索引处的值 private void exch(int i,int j){ T tmp = items[i]; items[i] = items[j]; items[j] = tmp; } //往堆中插入一个元素 public void insert(T t){ items[++N] = t; swim(N); } //删除堆中最大的元素,并返回这个最大元素 public T delMax(){ T max = items[1]; //交换索引1处和索引N处的值 exch(1,N); //删除最后位置上的元素 items[N]=null; N--;//个数-1 sink(1); return max; } //使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置 private void swim(int k){ //如果已经到了根结点,就不需要循环了 while(k>1){ //比较当前结点和其父结点 if(less(k/2,k)){ //父结点小于当前结点,需要交换 exch(k/2,k); } k = k/2; } } //使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置 private void sink(int k){ //如果当前已经是最底层了,就不需要循环了 while(2*k<=N){ //找到子结点中的较大者 int max; if (2*k+1<=N){//存在右子结点 if (less(2*k,2*k+1)){ max = 2*k+1; }else{ max = 2*k; } }else{//不存在右子结点 max = 2*k; } //比较当前结点和子结点中的较大者,如果当前结点不小,则结束循环 if (!less(k,max)){ break; } //当前结点小,则交换, exch(k,max); k = max; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { Heap<String> heap = new Heap<String>(20); heap.insert("S"); heap.insert("G"); heap.insert("I"); heap.insert("E"); heap.insert("N"); heap.insert("H"); heap.insert("O"); heap.insert("A"); heap.insert("T"); heap.insert("P"); heap.insert("R"); String del; while((del=heap.delMax())!=null){ System.out.print(del+","); } } }
1.4 堆排序

1.4.1 堆构造过程
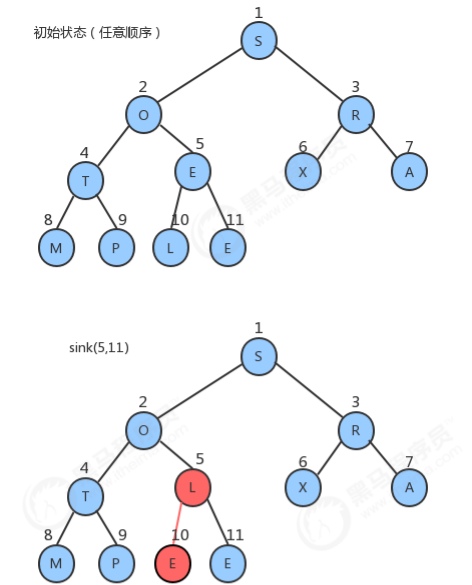

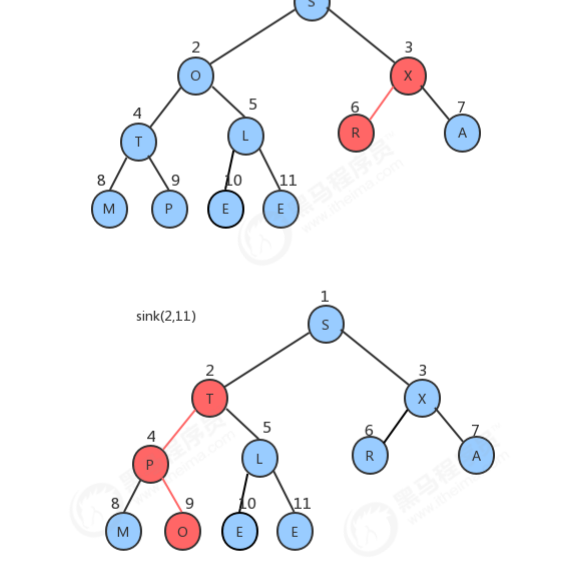
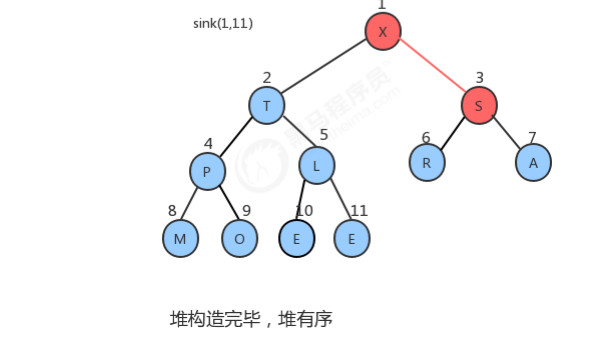
1.4.2 堆排序过程
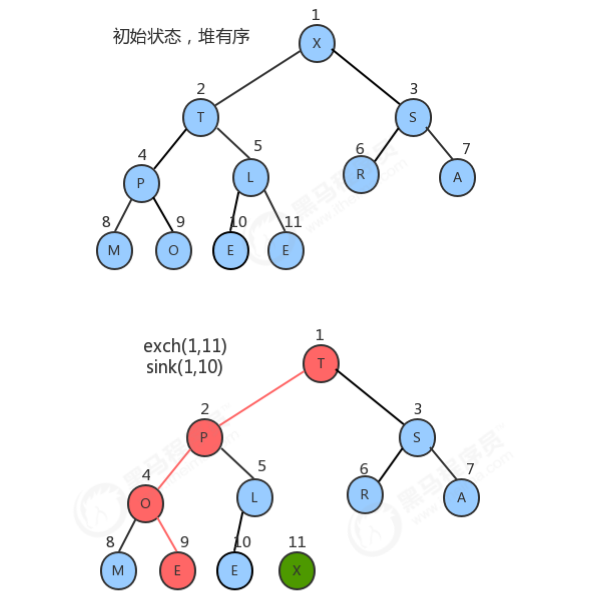
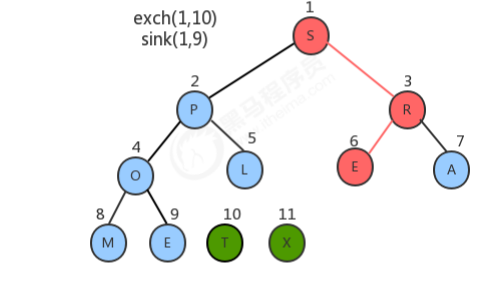
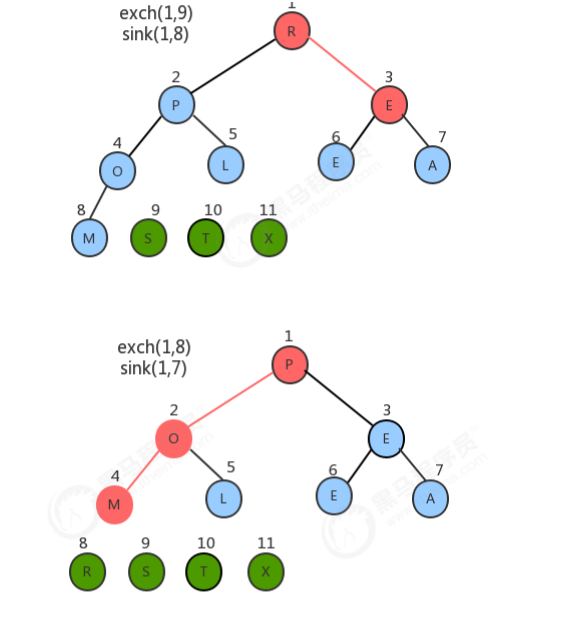


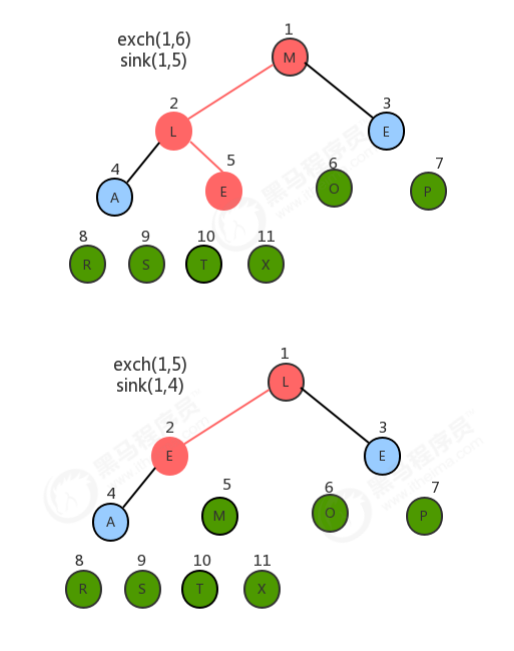

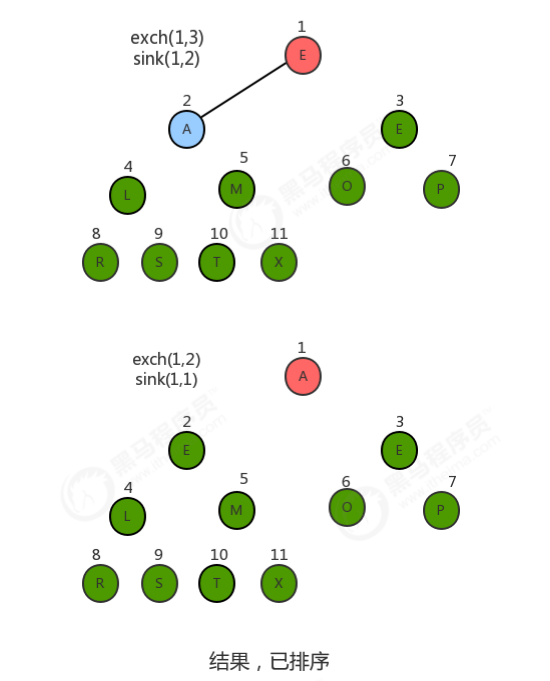
//对排序代码 public class HeapSort { //对source数组中的数据从小到大排序 public static void sort(Comparable[] source) { //1.创建一个比原数组大1的数组 Comparable[] heap = new Comparable[source.length + 1]; //2.构造堆 createHeap(source,heap); //3.堆排序 //3.1定义一个变量,记录heap中未排序的所有元素中最大的索引 int N = heap.length-1; while(N!=1){ //3.2交换heap中索引1处的元素和N处的元素 exch(heap,1,N); N--; //3.3对索引1处的元素在0~N范围内做下沉操作 sink(heap,1,N); } //4.heap中的数据已经有序,拷贝到source中 System.arraycopy(heap,1,source,0,source.length); } //根据原数组source,构造出堆heap private static void createHeap(Comparable[] source, Comparable[] heap) { //1.把source中的数据拷贝到heap中,从heap的1索引处开始填充 System.arraycopy(source,0,heap,1,source.length); //2.从heap索引的一半处开始倒叙遍历,对得到的每一个元素做下沉操作 for (int i = (heap.length-1)/2; i>0 ; i--) { sink(heap,i,heap.length-1); } } //判断heap堆中索引i处的元素是否小于索引j处的元素 private static boolean less(Comparable[] heap, int i, int j) { return heap[i].compareTo(heap[j])<0; } //交换heap堆中i索引和j索引处的值 private static void exch(Comparable[] heap, int i, int j) { Comparable tmp = heap[i]; heap[i] = heap[j]; heap[j] = tmp; } //在heap堆中,对target处的元素做下沉,范围是0~range private static void sink(Comparable[] heap, int target, int range){ //没有子结点了 while (2*target<=range){ //1.找出target结点的两个子结点中的较大值 int max=2*target; if (2*target+1<=range){ //存在右子结点 if (less(heap,2*target,2*target+1)){ max=2*target+1; } } //2.如果当前结点的值小于子结点中的较大值,则交换 if(less(heap,target,max)){ exch(heap,target,max); } //3.更新target的值 target=max; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"}; HeapSort.sort(arr); System.out.println(Arrays.toString(arr)); } }
一、优先队列
1.1 最大优先队列
1.1.1 最大优先队列API设计

1.1.2 最大优先队列代码实现
//最大优先队列代码 public class MaxPriorityQueue<T extends Comparable<T>> { //存储堆中的元素 private T[] items; //记录堆中元素的个数 private int N; public MaxPriorityQueue(int capacity) { items = (T[]) new Comparable[capacity+1]; N = 0; } //获取队列中元素的个数 public int size() { return N; } //判断队列是否为空 public boolean isEmpty() { return N == 0; } //判断堆中索引i处的元素是否小于索引j处的元素 private boolean less(int i, int j) { return items[i].compareTo(items[j]) < 0; } //交换堆中i索引和j索引处的值 private void exch(int i, int j) { T tmp = items[i]; items[i] = items[j]; items[j] = tmp; } //往堆中插入一个元素 public void insert(T t) { items[++N] = t; swim(N); } //删除堆中最大的元素,并返回这个最大元素 public T delMax() { T max = items[1]; //交换索引1处和索引N处的值 exch(1, N); //删除最后位置上的元素 items[N] = null; N--;//个数-1 sink(1); return max; } //使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置 private void swim(int k) { //如果已经到了根结点,就不需要循环了 while (k > 1) { //比较当前结点和其父结点 if (less(k / 2, k)) { //父结点小于当前结点,需要交换 exch(k / 2, k); } k = k / 2; } } //使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置 private void sink(int k) { //如果当前已经是最底层了,就不需要循环了 while (2 * k <= N) { //找到子结点中的较大者 int max = 2 * k; if (2 * k + 1 <= N) {//存在右子结点 if (less(2 * k, 2 * k + 1)) { max = 2 * k + 1; } } //比较当前结点和子结点中的较大者,如果当前结点不小,则结束循环 if (!less(k, max)) { break; } //当前结点小,则交换, exch(k, max); k = max; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"}; MaxPriorityQueue<String> maxpq = new MaxPriorityQueue<>(20); for (String s : arr) { maxpq.insert(s); } System.out.println(maxpq.size()); String del; while(!maxpq.isEmpty()){ del = maxpq.delMax(); System.out.print(del+","); } } }
1.2 最小优先队列
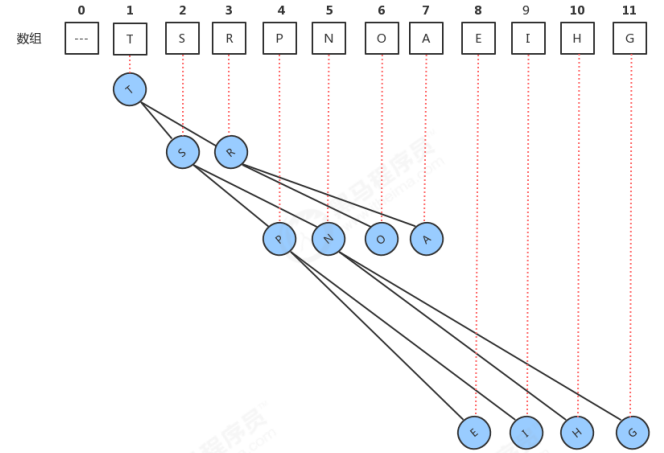

1.2.1 最小优先队列API设计
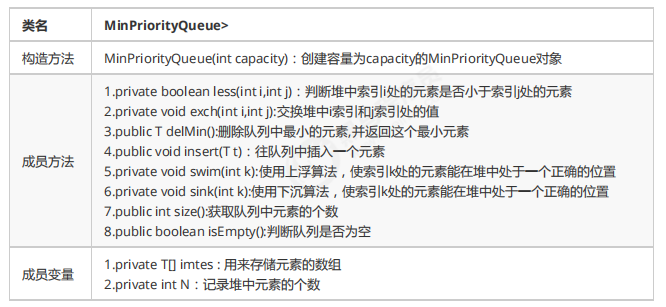
1.2.2 最小优先队列代码实现
//最小优先队列代码 public class MinPriorityQueue<T extends Comparable<T>> { //存储堆中的元素 private T[] items; //记录堆中元素的个数 private int N; public MinPriorityQueue(int capacity) { items = (T[]) new Comparable[capacity+1]; N = 0; } //获取队列中元素的个数 public int size() { return N; } //判断队列是否为空 public boolean isEmpty() { return N == 0; } //判断堆中索引i处的元素是否小于索引j处的元素 private boolean less(int i, int j) { return items[i].compareTo(items[j]) < 0; } //交换堆中i索引和j索引处的值 private void exch(int i, int j) { T tmp = items[i]; items[i] = items[j]; items[j] = tmp; } //往堆中插入一个元素 public void insert(T t) { items[++N] = t; swim(N); } //删除堆中最小的元素,并返回这个最小元素 public T delMin() { //索引1处的值是最小值 T min = items[1]; //交换索引1处和索引N处的值 exch(1, N); //删除索引N处的值 items[N] = null; //数据元素-1 N--; //对索引1处的值做下沉,使堆重新有序 sink(1); //返回被删除的值 return min; } //使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置 private void swim(int k) { //如果没有父结点,则不再上浮 while (k > 1) { //如果当前结点比父结点小,则交换 if (less(k, k / 2)) { exch(k, k / 2); } k = k / 2; } } //使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置 private void sink(int k) { //如果没有子结点,则不再下沉 while (2 * k <= N) { //找出子结点中的较小值的索引 int min = 2 * k; if (2 * k + 1 <= N && less(2 * k + 1, 2 * k)) { min = 2 * k + 1; } //如果当前结点小于子结点中的较小值,则结束循环 if (less(k, min)) { break; } //当前结点大,交换 exch(min, k); k = min; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"}; MinPriorityQueue<String> minpq = new MinPriorityQueue<>(20); for (String s : arr) { minpq.insert(s); } System.out.println(minpq.size()); String del; while(!minpq.isEmpty()){ del = minpq.delMin(); System.out.print(del+","); } } }
1.3 索引优先队列
1.3.1 索引优先队列实现思路

步骤二:
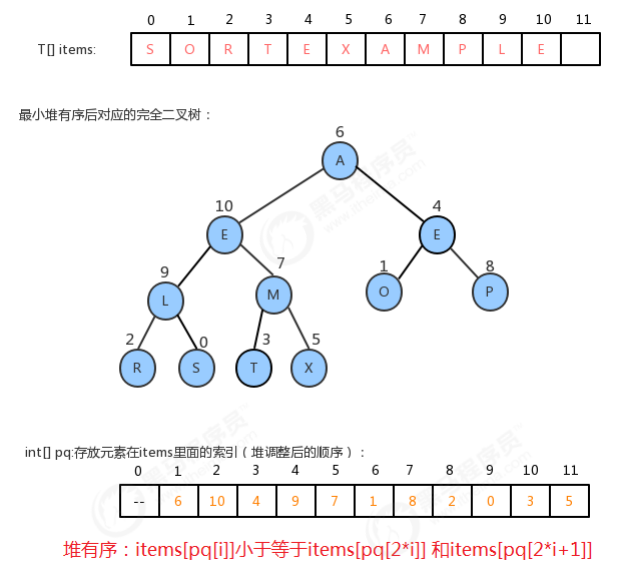
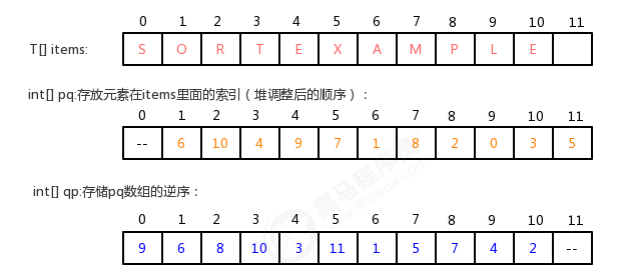
1.3.2 索引优先队列API设计

1.3.3 索引优先队列代码实现
//最小索引优先队列代码 package cn.itcast; public class IndexMinPriorityQueue<T extends Comparable<T>> { //存储堆中的元素 private T[] items; //保存每个元素在items数组中的索引,pq数组需要堆有序 private int[] pq; //保存qp的逆序,pq的值作为索引,pq的索引作为值 private int[] qp; //记录堆中元素的个数 private int N; public IndexMinPriorityQueue(int capacity) { items = (T[]) new Comparable[capacity + 1]; pq = new int[capacity + 1]; qp = new int[capacity + 1]; N = 0; for (int i = 0; i < qp.length; i++) { //默认情况下,qp逆序中不保存任何索引 qp[i] = -1; } } //获取队列中元素的个数 public int size() { return N; } //判断队列是否为空 public boolean isEmpty() { return N == 0; } //判断堆中索引i处的元素是否小于索引j处的元素 private boolean less(int i, int j) { //先通过pq找出items中的索引,然后再找出items中的元素进行对比 return items[pq[i]].compareTo(items[pq[j]]) < 0; } //交换堆中i索引和j索引处的值 private void exch(int i, int j) { //先交换pq数组中的值 int tmp = pq[i]; pq[i] = pq[j]; pq[j] = tmp; //更新qp数组中的值 qp[pq[i]] = i; qp[pq[j]] = j; } //判断k对应的元素是否存在 public boolean contains(int k) { //默认情况下,qp的所有元素都为-1,如果某个位置插入了数据,则不为-1 return qp[k] != -1; } //最小元素关联的索引 public int minIndex() { //pq的索引1处,存放的是最小元素在items中的索引 return pq[1]; } //往队列中插入一个元素,并关联索引i public void insert(int i, T t) { //如果索引i处已经存在了元素,则不让插入 if (contains(i)) { throw new RuntimeException("该索引已经存在"); } //个数+1 N++; //把元素存放到items数组中 items[i] = t; //使用pq存放i这个索引 pq[N] = i; //在qp的i索引处存放N qp[i] = N; //上浮items[pq[N]],让pq堆有序 swim(N); } //删除队列中最小的元素,并返回该元素关联的索引 public int delMin() { //找到items中最小元素的索引 int minIndex = pq[1]; //交换pq中索引1处的值和N处的值 exch(1, N); //删除qp中索引pq[N]处的值 qp[pq[N]] = -1; //删除pq中索引N处的值 pq[N] = -1; //删除items中的最小元素 items[minIndex] = null; //元素数量-1 N--; //对pq[1]做下沉,让堆有序 sink(1); return minIndex; } //删除索引i关联的元素 public void delete(int i) { //找出i在pq中的索引 int k = qp[i]; //把pq中索引k处的值和索引N处的值交换 exch(k, N); //删除qp中索引pq[N]处的值 qp[pq[N]] = -1; //删除pq中索引N处的值 pq[N] = -1; //删除items中索引i处的值 items[i] = null; //元素数量-1 N--; //对pq[k]做下沉,让堆有序 sink(k); //对pq[k]做上浮,让堆有序 swim(k); } //把与索引i关联的元素修改为为t public void changeItem(int i, T t) { //修改items数组中索引i处的值为t items[i] = t; //找到i在pq中的位置 int k = qp[i]; //对pq[k]做下沉,让堆有序 sink(k); //对pq[k]做上浮,让堆有序 swim(k); } //使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置 private void swim(int k) { //如果已经到了根结点,则结束上浮 while (k > 1) { //比较当前结点和父结点,如果当前结点比父结点小,则交换位置 if (less(k, k / 2)) { exch(k, k / 2); } k = k / 2; } } //使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置 private void sink(int k) { //如果当前结点已经没有子结点了,则结束下沉 while (2 * k <= N) { //找出子结点中的较小值 int min = 2 * k; if (2 * k + 1 <= N && less(2 * k + 1, 2 * k)) { min = 2 * k + 1; } //如果当前结点的值比子结点中的较小值小,则结束下沉 if (less(k, min)) { break; } exch(k, min); k = min; } } } //测试代码 public class Test { public static void main(String[] args) { String[] arr = {"S", "O", "R", "T", "E", "X", "A", "M", "P", "L", "E"}; IndexMinPriorityQueue<String> indexMinPQ = new IndexMinPriorityQueue<>(20); //插入 for (int i = 0; i < arr.length; i++) { indexMinPQ.insert(i,arr[i]); } System.out.println(indexMinPQ.size()); //获取最小值的索引 System.out.println(indexMinPQ.minIndex()); //测试修改 indexMinPQ.changeItem(0,"Z"); int minIndex=-1; while(!indexMinPQ.isEmpty()){ minIndex = indexMinPQ.delMin(); System.out.print(minIndex+","); } } }
一、平衡树
1.1 2-3查找树
1.1.1 2-3查找树的定义
2-结点:
3-结点:
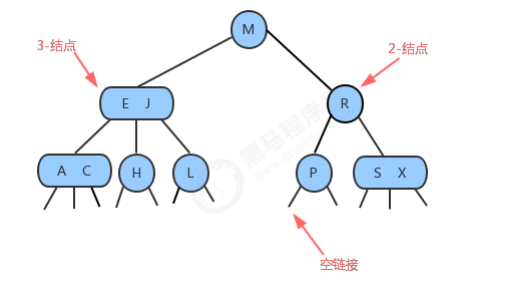
1.1.2 查找

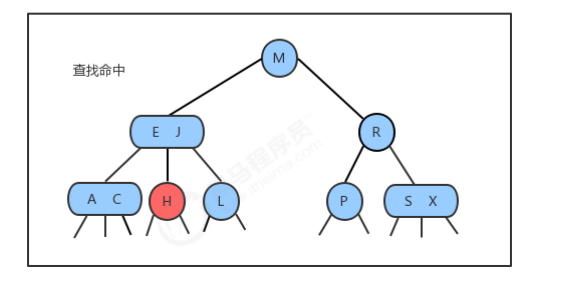
1.1.3 插入
1.1.3.1 向2-结点中插入新键
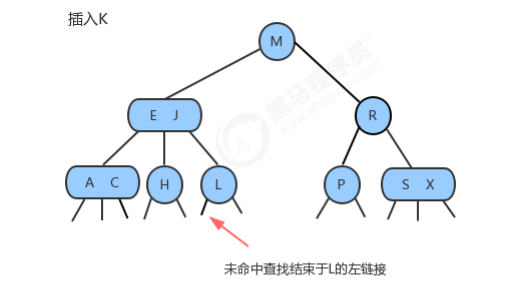
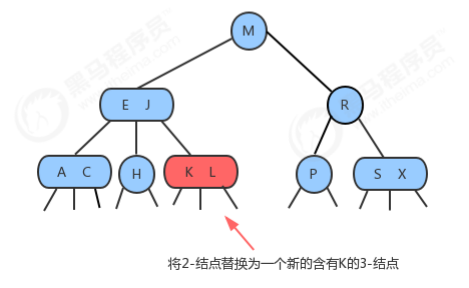
1.1.3.2 向一棵只含有一个3-结点的树中插入新键
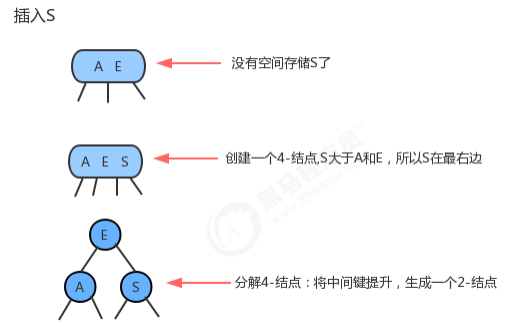
1.1.3.3 向一个父结点为2-结点的3-结点中插入新键

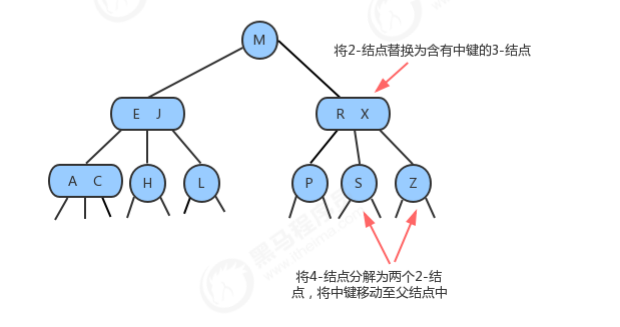
1.3.1.4 向一个父结点为3-结点的3-结点中插入新键
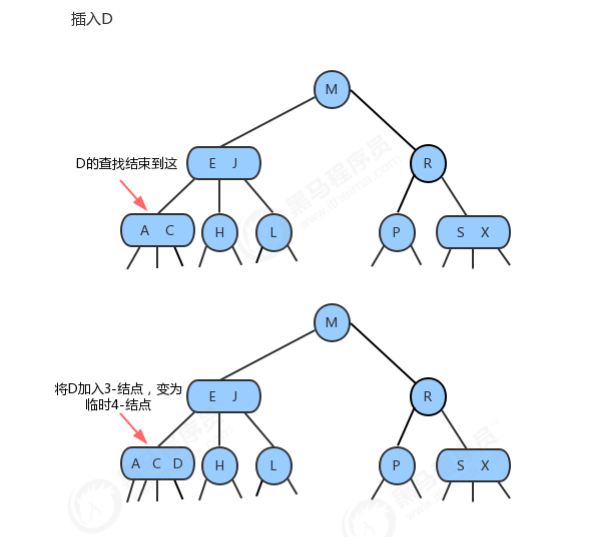

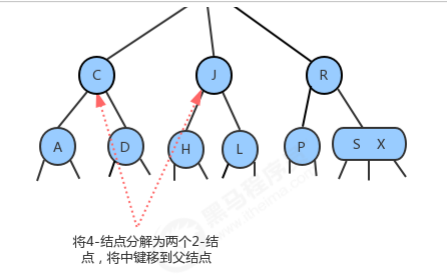
1.3.1.5 分解根结点
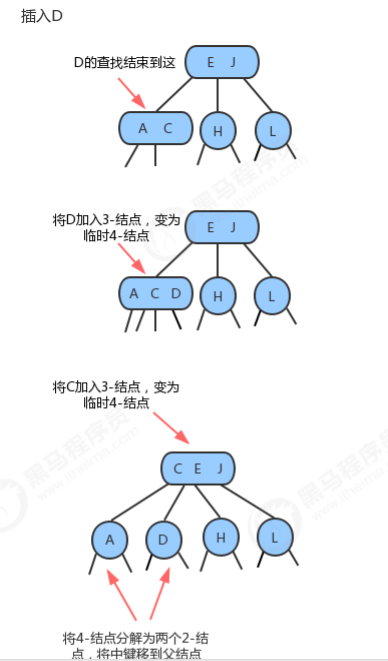
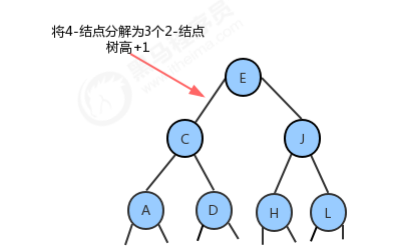
1.3.4 2-3树的性质
1.3.5 2-3树的实现
1.2 红黑树

1.2.1 红黑树的定义
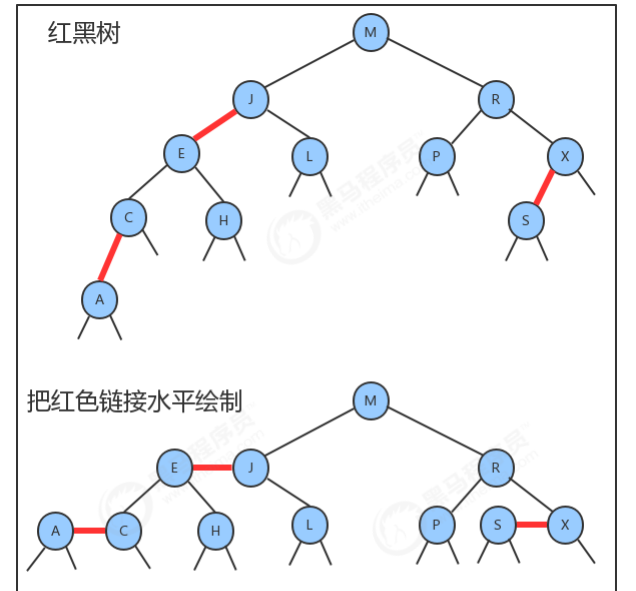

1.2.2 红黑树结点API


private class Node<Key,Value>{ //存储键 public Key key; //存储值 private Value value; //记录左子结点 public Node left; //记录右子结点 public Node right; //由其父结点指向它的链接的颜色 public boolean color; public Node(Key key, Value value, Node left,Node right,boolean color) { this.key = key; this.value = value; this.left = left; this.right = right; this.color = color; } }
1.2.3 平衡化
1.2.3.1 左旋
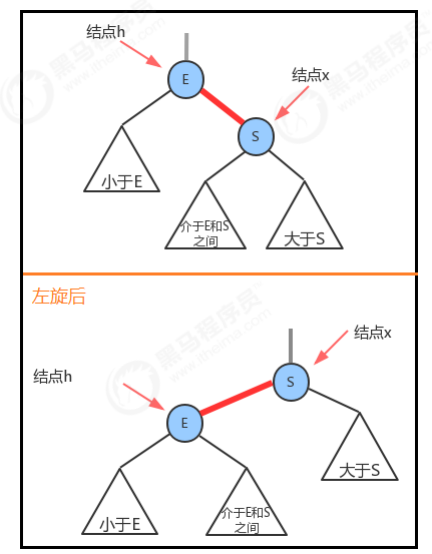
1.2.3.2 右旋
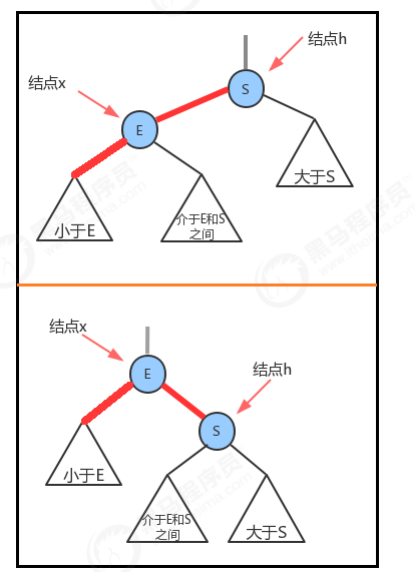
1.2.4 向单个2-结点中插入新键
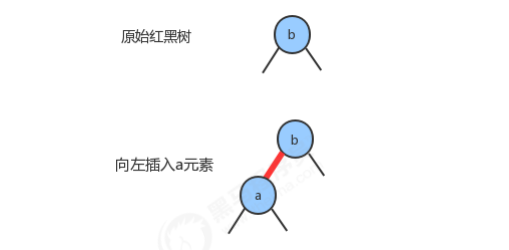

1.2.5 向底部的2-结点插入新键
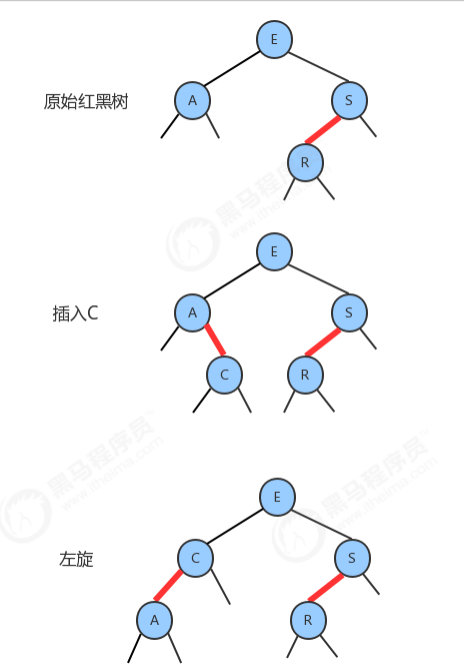
1.2.6 颜色反转

1.2.7 向一棵双键树(即一个3-结点)中插入新键
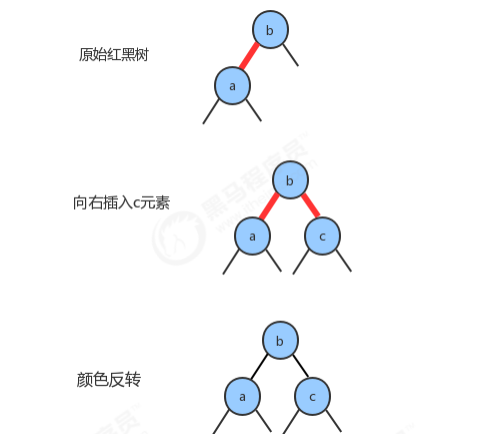
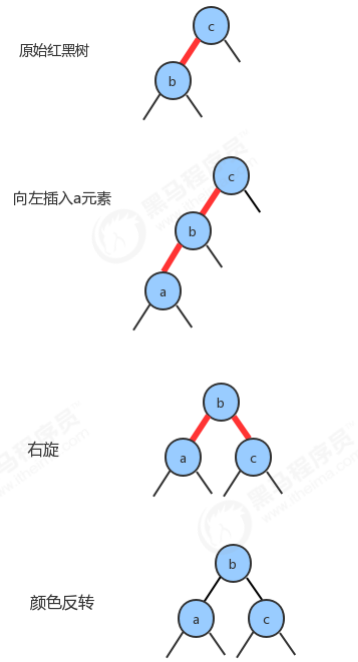
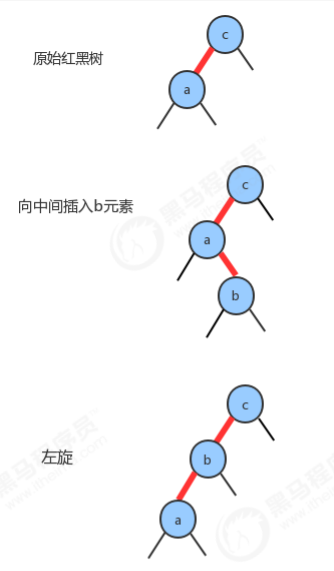
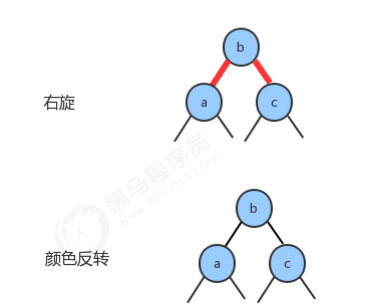
1.2.8 根结点的颜色总是黑色
1.2.9 向树底部的3-结点插入新键

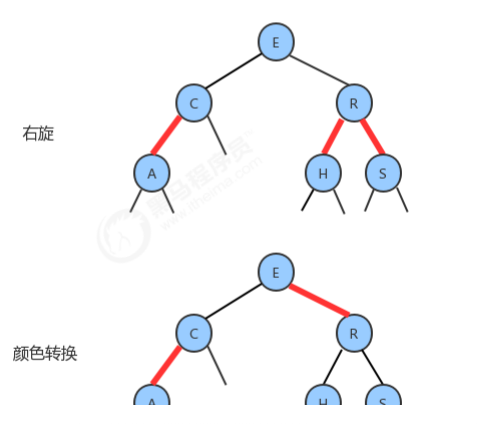
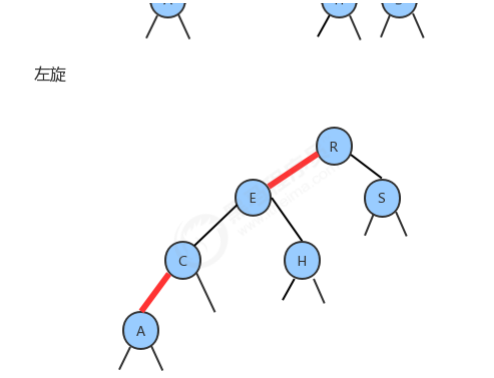
1.2.10 红黑树的API设计

1.2.11 红黑树的实现
//红黑树代码 public class RedBlackTree<Key extends Comparable<Key>, Value> { //根节点 private Node root; //记录树中元素的个数 private int N; //红色链接 private static final boolean RED = true; //黑色链接 private static final boolean BLACK = false; /** * 判断当前节点的父指向链接是否为红色 * * @param x * @return */ private boolean isRed(Node x) { //空结点默认是黑色链接 if (x == null) { return false; } //非空结点需要判断结点color属性的值 return x.color == RED; } /** * 左旋转 * * @param h * @return */ private Node rotateLeft(Node h) { //找出当前结点h的右子结点 Node hRight = h.right; //找出右子结点的左子结点 Node lhRight = hRight.left; //让当前结点h的右子结点的左子结点成为当前结点的右子结点 h.right = lhRight; //让当前结点h称为右子结点的左子结点 hRight.left = h; //让当前结点h的color编程右子结点的color hRight.color = h.color; //让当前结点h的color变为RED h.color = RED; //返回当前结点的右子结点 return hRight; } /** * 右旋 * * @param h * @return */ private Node rotateRight(Node h) { //找出当前结点h的左子结点 Node hLeft = h.left; //找出当前结点h的左子结点的右子结点 Node rHleft = hLeft.right; //让当前结点h的左子结点的右子结点称为当前结点的左子结点 h.left = rHleft; //让当前结点称为左子结点的右子结点 hLeft.right = h; //让当前结点h的color值称为左子结点的color值 hLeft.color = h.color; //让当前结点h的color变为RED h.color = RED; //返回当前结点的左子结点 return hLeft; } /** * 颜色反转,相当于完成拆分4-节点 * * @param h */ private void flipColors(Node h) { //当前结点的color属性值变为RED; h.color = RED; //当前结点的左右子结点的color属性值都变为黑色 h.left.color = BLACK; h.right.color = BLACK; } /** * 在整个树上完成插入操作 * * @param key * @param val */ public void put(Key key, Value val) { //在root整个树上插入key-val root = put(root, key, val); //让根结点的颜色变为BLACK root.color = BLACK; } /** * 在指定树中,完成插入操作,并返回添加元素后新的树 * * @param h * @param key * @param val */ private Node put(Node h, Key key, Value val) { if (h == null) { //标准的插入操作,和父结点用红链接相连 N++; return new Node(key, val, null, null, RED); } //比较要插入的键和当前结点的键 int cmp = key.compareTo(h.key); if (cmp < 0) { //继续寻找左子树插入 h.left = put(h.left, key, val); } else if (cmp > 0) { //继续寻找右子树插入 h.right = put(h.right, key, val); } else { //已经有相同的结点存在,修改节点的值; h.value = val; } //如果当前结点的右链接是红色,左链接是黑色,需要左旋 if (isRed(h.right) && !isRed(h.left)) { h=rotateLeft(h); } //如果当前结点的左子结点和左子结点的左子结点都是红色链接,则需要右旋 if (isRed(h.left) && isRed(h.left.left)) { h=rotateRight(h); } //如果当前结点的左链接和右链接都是红色,需要颜色变换 if (isRed(h.left) && isRed(h.right)) { flipColors(h); } //返回当前结点 return h; } //根据key,从树中找出对应的值 public Value get(Key key) { return get(root, key); } //从指定的树x中,查找key对应的值 public Value get(Node x, Key key) { //如果当前结点为空,则没有找到,返回null if (x == null) { return null; } //比较当前结点的键和key int cmp = key.compareTo(x.key); if (cmp < 0) { //如果要查询的key小于当前结点的key,则继续找当前结点的左子结点; return get(x.left, key); } else if (cmp > 0) { //如果要查询的key大于当前结点的key,则继续找当前结点的右子结点; return get(x.right, key); } else { //如果要查询的key等于当前结点的key,则树中返回当前结点的value。 return x.value; } } //获取树中元素的个数 public int size() { return N; } //结点类 private class Node { //存储键 public Key key; //存储值 private Value value; //记录左子结点 public Node left; //记录右子结点 public Node right; //由其父结点指向它的链接的颜色 public boolean color; public Node(Key key, Value value, Node left, Node right, boolean color) { this.key = key; this.value = value; this.left = left; this.right = right; this.color = color; } } } //测试代码 public class Test { public static void main(String[] args) throws Exception { RedBlackTree<Integer, String> bt = new RedBlackTree<>(); bt.put(4, "二哈"); bt.put(1, "张三"); bt.put(3, "李四"); bt.put(5, "王五"); System.out.println(bt.size()); bt.put(1,"老三"); System.out.println(bt.get(1)); System.out.println(bt.size()); } }
二、B-树
1.1 B树的特性

2.2 B树存储数据

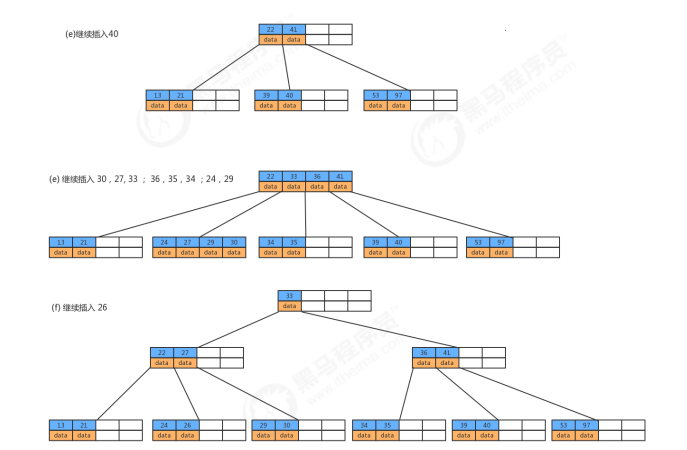
2.3 B树在磁盘文件中的应用
2.3.1 磁盘
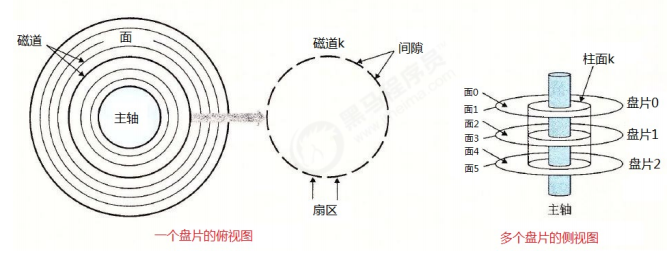
2.3.2 磁盘IO
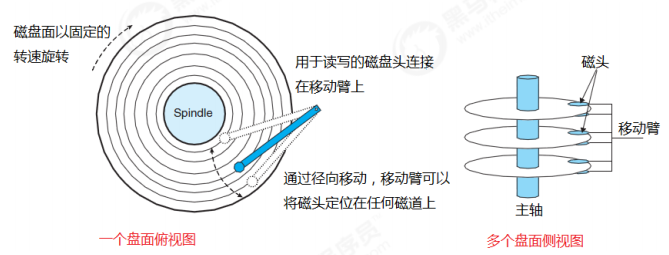
三、 B+树
2.1 B+树存储数据
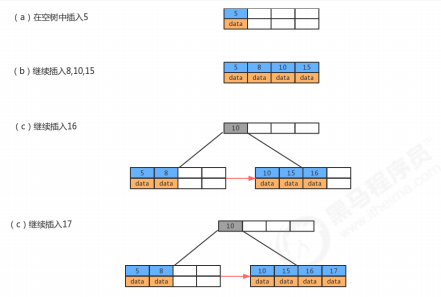
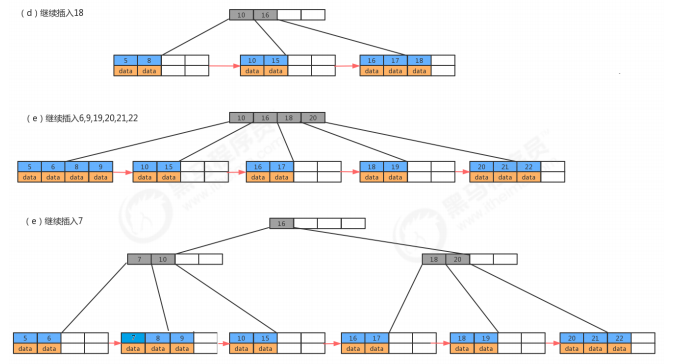
2.2 B+树和B树的对比
3.3 B+树在数据库中的应用
3.3.1 未建立主键索引查询
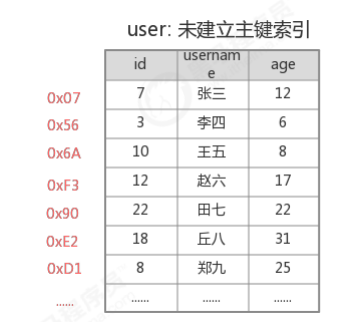
3.3.2 建立主键索引查询
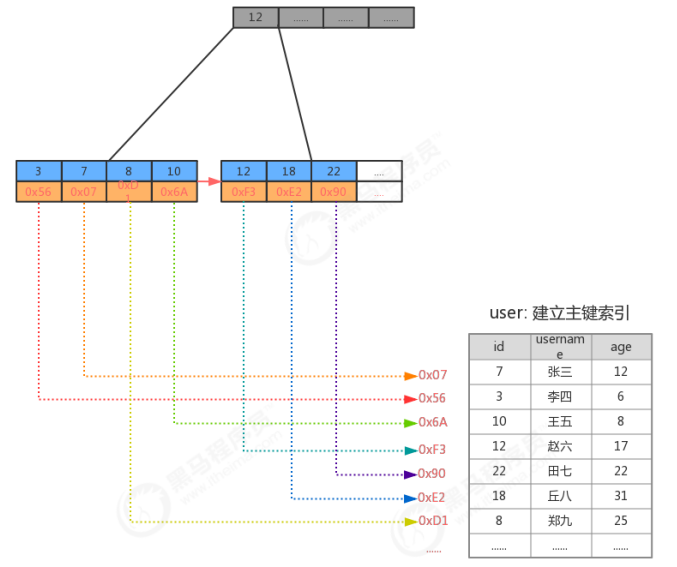
3.3.3 区间查询
一、并查集

1.1 并查集结构
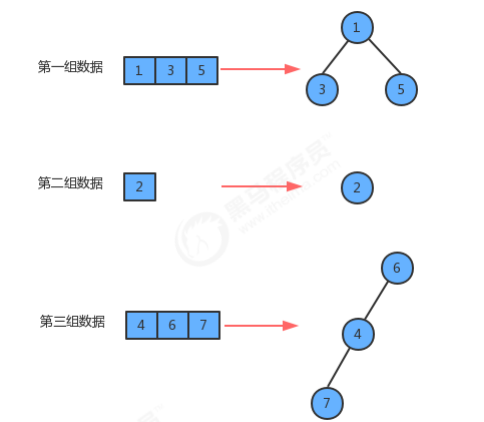
1.2 并查集API设计

1.3 并查集的实现
1.3.1 UF(int N)构造方法实现
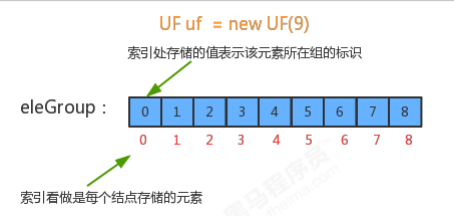
1.3.2 union(int p,int q)合并方法实现

3.3.3 代码
//并查集代码 public class UF { //记录结点元素和该元素所在分组的标识 private int[] eleAndGroup; //记录并查集中数据的分组个数 private int count; //初始化并查集 public UF(int N){ //初始情况下,每个元素都在一个独立的分组中,所以,初始情况下,并查集中的数据默认分为N个组 this.count=N; //初始化数组 eleAndGroup = new int[N]; //把eleAndGroup数组的索引看做是每个结点存储的元素,把eleAndGroup数组每个索引处的值看做是该 结点所在的分组,那么初始化情况下,i索引处存储的值就是i for (int i = 0; i < N; i++) { eleAndGroup[i]=i; } } //获取当前并查集中的数据有多少个分组 public int count(){ return count; } //元素p所在分组的标识符 public int find(int p){ return eleAndGroup[p]; } //判断并查集中元素p和元素q是否在同一分组中 public boolean connected(int p,int q){ return find(p)==find(q); } //把p元素所在分组和q元素所在分组合并 public void union(int p,int q){ //如果p和q已经在同一个分组中,则无需合并; if (connected(p,q)){ return; } //如果p和q不在同一个分组,则只需要将p元素所在组的所有的元素的组标识符修改为q元素所在组的标识 符即可 int pGroup = find(p); int qGroup = find(q); for (int i = 0; i < eleAndGroup.length; i++) { if (eleAndGroup[i]==pGroup){ eleAndGroup[i]=qGroup; } } //分组数量-1 count--; } } //测试代码 public class Test { public static void main(String[] args) { Scanner sc = new Scanner(System.in); System.out.println("请录入并查集中元素的个数:"); int N = sc.nextInt(); UF uf = new UF(N); while(true){ System.out.println("请录入您要合并的第一个点:"); int p = sc.nextInt(); System.out.println("请录入您要合并的第二个点:"); int q = sc.nextInt(); //判断p和q是否在同一个组 if (uf.connected(p,q)){ System.out.println("结点:"+p+"结点"+q+"已经在同一个组"); continue; } uf.union(p,q); System.out.println("总共还有"+uf.count()+"个分组"); } } }
1.3.4 并查集应用举例
1.3.5 UF_Tree算法优化
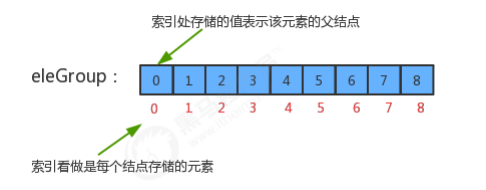
1.3.5.1 UF_Tree API设计

1.3.5.2 fifind(int p)查询方法实现
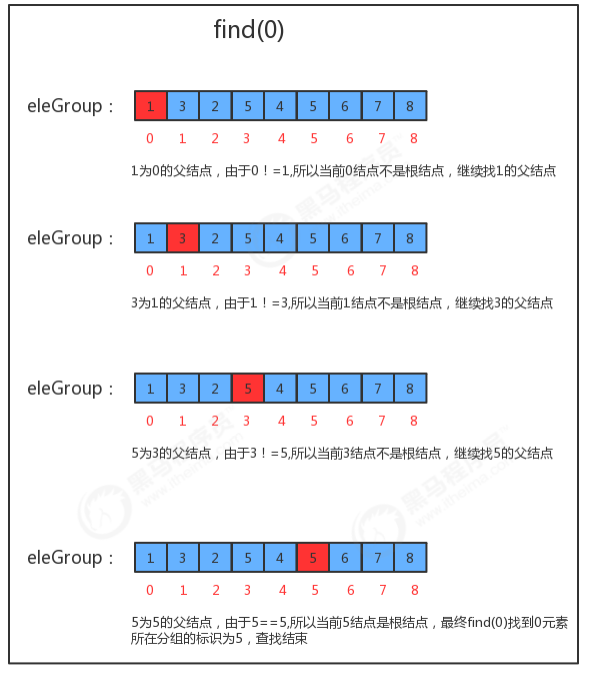
1.3.5.3 union(int p,int q)合并方法实现
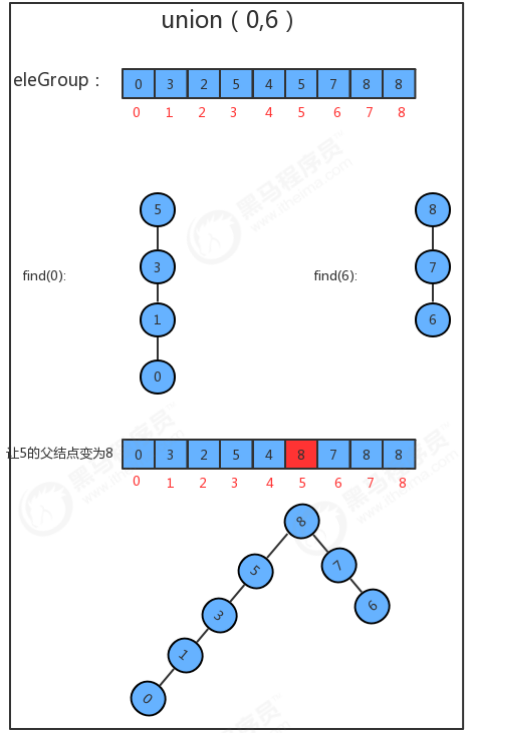
1.3.5.4 代码
package cn.itcast; public class UF_Tree { //记录结点元素和该元素所的父结点 private int[] eleAndGroup; //记录并查集中数据的分组个数 private int count; //初始化并查集 public UF_Tree(int N){ //初始情况下,每个元素都在一个独立的分组中,所以,初始情况下,并查集中的数据默认分为N个组 this.count=N; //初始化数组 eleAndGroup = new int[N]; //把eleAndGroup数组的索引看做是每个结点存储的元素,把eleAndGroup数组每个索引处的值看做是该 结点的父结点,那么初始化情况下,i索引处存储的值就是i for (int i = 0; i < N; i++) { eleAndGroup[i]=i; } } //获取当前并查集中的数据有多少个分组 public int count(){ return count; } //元素p所在分组的标识符 public int find(int p){ while(true){ //判断当前元素p的父结点eleAndGroup[p]是不是自己,如果是自己则证明已经是根结点了; if (p==eleAndGroup[p]){ return p; } //如果当前元素p的父结点不是自己,则让p=eleAndGroup[p],继续找父结点的父结点,直到找到根 结点为止; p=eleAndGroup[p]; } } //判断并查集中元素p和元素q是否在同一分组中 public boolean connected(int p,int q){ return find(p)==find(q); } //把p元素所在分组和q元素所在分组合并 public void union(int p,int q){ //找到p元素所在树的根结点 int pRoot = find(p); //找到q元素所在树的根结点 int qRoot = find(q); //如果p和q已经在同一个树中,则无需合并; if (pRoot==qRoot){ return; } //如果p和q不在同一个分组,则只需要将p元素所在树根结点的父结点设置为q元素的根结点即可; eleAndGroup[pRoot]=qRoot; //分组数量-1 count--; } }
1.3.5.5 优化后的性能分析

1.3.6 路径压缩

1.3.6.1 UF_Tree_Weighted API设计

1.3.6.2 代码
public class UF_Tree_Weighted { //记录结点元素和该元素所的父结点 private int[] eleAndGroup; //存储每个根结点对应的树中元素的个数 private int[] sz; //记录并查集中数据的分组个数 private int count; //初始化并查集 public UF_Tree_Weighted(int N){ //初始情况下,每个元素都在一个独立的分组中,所以,初始情况下,并查集中的数据默认分为N个组 this.count=N; //初始化数组 eleAndGroup = new int[N]; sz = new int[N]; //把eleAndGroup数组的索引看做是每个结点存储的元素,把eleAndGroup数组每个索引处的值看做是该 结点的父结点,那么初始化情况下,i索引处存储的值就是i for (int i = 0; i < N; i++) { eleAndGroup[i]=i; } //把sz数组中所有的元素初始化为1,默认情况下,每个结点都是一个独立的树,每个树中只有一个元素 for (int i = 0; i < sz.length; i++) { sz[i]=1; } } //获取当前并查集中的数据有多少个分组 public int count(){ return count; } //元素p所在分组的标识符 public int find(int p){ while(true){ //判断当前元素p的父结点eleAndGroup[p]是不是自己,如果是自己则证明已经是根结点了; if (p==eleAndGroup[p]){ return p; } //如果当前元素p的父结点不是自己,则让p=eleAndGroup[p],继续找父结点的父结点,直到找到根 结点为止; p=eleAndGroup[p]; } } //判断并查集中元素p和元素q是否在同一分组中 public boolean connected(int p,int q){ return find(p)==find(q); } //把p元素所在分组和q元素所在分组合并 public void union(int p,int q){ //找到p元素所在树的根结点 int pRoot = find(p); //找到q元素所在树的根结点 int qRoot = find(q); //如果p和q已经在同一个树中,则无需合并; if (pRoot==qRoot){ return; } //如果p和q不在同一个分组,比较p所在树的元素个数和q所在树的元素个数,把较小的树合并到较大的树 上 if (sz[pRoot]<sz[qRoot]){ eleAndGroup[pRoot] = qRoot; //重新调整较大树的元素个数 sz[qRoot]+=sz[pRoot]; }else{ eleAndGroup[qRoot]=pRoot; sz[pRoot]+=sz[qRoot]; } //分组数量-1 count--; } }
1.3.7 案例-畅通工程

public class Traffic_Project { public static void main(String[] args)throws Exception { //创建输入流 BufferedReader reader = new BufferedReader(new InputStreamReader(Traffic_Project.class.getClassLoader().getResourceAsStream("traffic_projec t.txt"))); //读取城市数目,初始化并查集 int number = Integer.parseInt(reader.readLine()); UF_Tree_Weighted uf = new UF_Tree_Weighted(number); //读取已经修建好的道路数目 int roadNumber = Integer.parseInt(reader.readLine()); //循环读取已经修建好的道路,并调用union方法 for (int i = 0; i < roadNumber; i++) { String line = reader.readLine(); int p = Integer.parseInt(line.split(" ")[0]); int q = Integer.parseInt(line.split(" ")[1]); uf.union(p,q); } //获取剩余的分组数量 int groupNumber = uf.count(); //计算出还需要修建的道路 System.out.println("还需要修建"+(groupNumber-1)+"道路,城市才能相通"); } }
【数据结构】线段树(Segment Tree)
假设我们现在拿到了一个非常大的数组,对于这个数组里面的数字要反复不断地做两个操作。

1、(query)随机在这个数组中选一个区间,求出这个区间所有数的和。
2、(update)不断地随机修改这个数组中的某一个值。

时间复杂度:
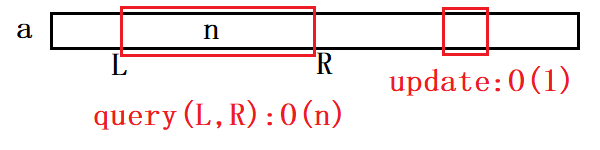
枚举:
枚举L~R的每个数并累加。
- query:O(n)
找到要修改的数直接修改。
- update:O(1)
如果query与update要做很多很多次,query的O(n)会被卡住,所以时间复杂度会非常慢。那么有没有办法把query的时间复杂度降成O(1)呢?其中一种方法如下:
- 先建立一个与a数组一样大的数组。
- s[1]=a[1];s[2]=a[1]+a[2];s[3]=a[1]+a[2]+a[3];...;s[n]=a[1]+a[2]+a[3]+...+a[n](在s数组中存入a的前缀和)
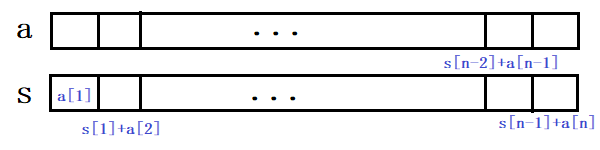
- 此时a[L]+a[L+1]+...+a[R]=s[R]-s[L-1],query的时间复杂度降为O(1)。
- 但若要修改a[k]的值,随之也需修改s[k],s[k+1],...,s[n]的值,时间复杂度升为O(n)。
前缀和:
query:O(1)
update:O(n)
- 我们发现,当我们想尽方法把其中一个操作的时间复杂度改成O(1)后,另一个操作的时间复杂度就会变为O(n)。当query与update的操作特别多时,不论用哪种方法,总体的时间复杂度都不会特别快。
- 所以,我们将要讨论一种叫线段树的数据结构,它可以把这两个操作的时间复杂度平均一下,使得query和update的时间复杂度都落在O(n log n)上,从而增加整个算法的效率。
线段树
假设我们拿到了如下长度为6的数组:

在构建线段树之前,我们先阐述线段树的性质:
1、线段树的每个节点都代表一个区间。
2、线段树具有唯一的根节点,代表的区间是整个统计范围,如[1,N]。
3、线段树的每个叶节点都代表一个长度为1的元区间[x,x]。
4、对于每个内部节点[l,r],它的左子结点是[l,mid],右子节点是[mid+1,r],其中mid=(l+r)/2(向下取整)。
依照这个数组,我们构建如下线段树(结点的性质为sum):
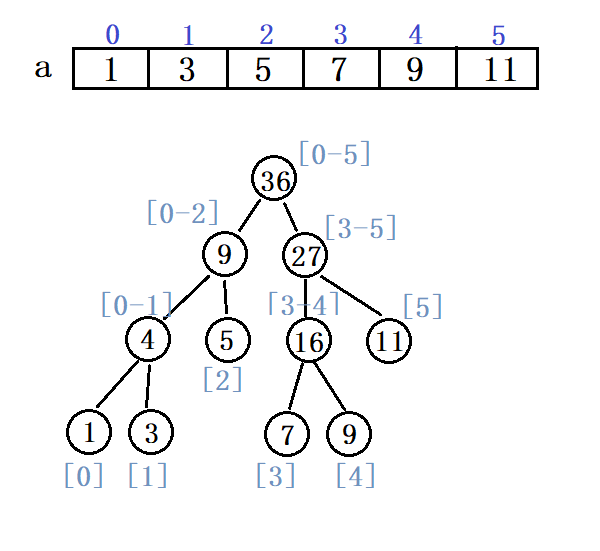
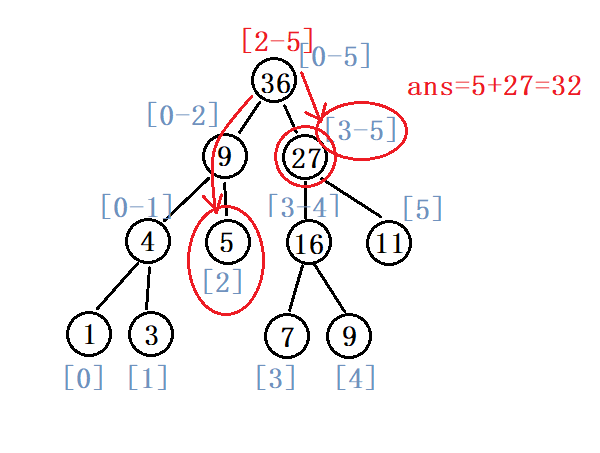
若我们要求[2-5]区间中数的和:
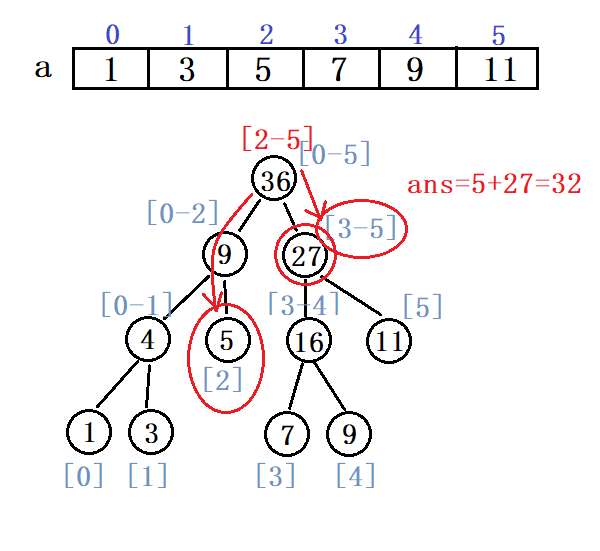
若我们要把a[4]改为6:
- 先一层一层找到目标节点修改,在依次向上修改当前节点的父节点。
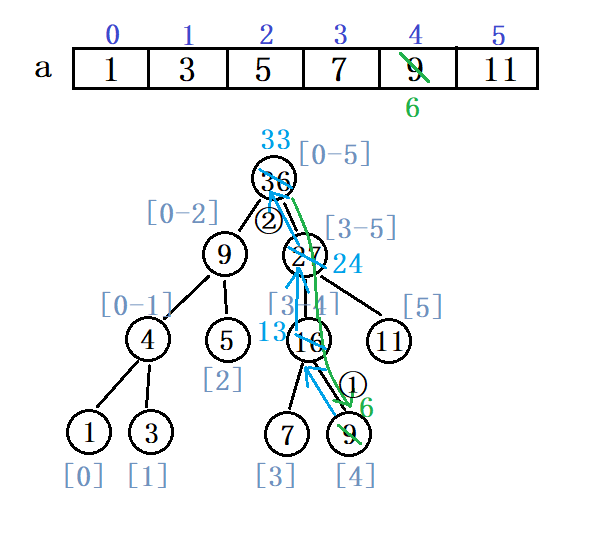
接下来的问题是:如何保存这棵线段树?
- 用数组存储。
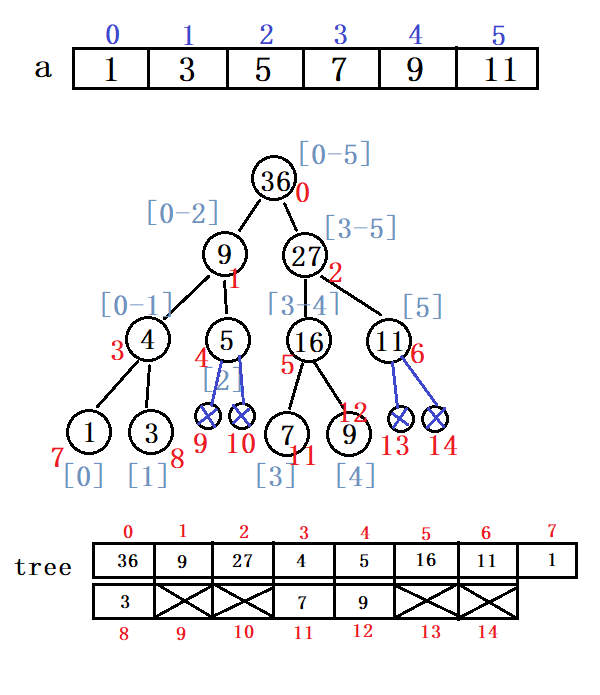
若我们要取node结点的左子结点(left)与右子节点(right),方法如下:
- left=2*node+1
- right=2*ndoe+2
举结点5为例(左子结点为节点11,右子节点为节点12):
- left5=2*5+1=11
- right5=2*5+2=12
接下来给出建树的代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1000;
int a[] = {1, 3, 5, 7, 9, 11};
int size = 6;
int tree[N] = {0};
//建立范围为a[start]~a[end]
void build(int a[], int tree[], int node/*当前节点*/, int start, int end){
//递归边界(即遇到叶子节点时)
if (start == end){
//直接存储a数组中的值
tree[node] = a[start];
}
else {
//将建立的区间分成两半
int mid = (start + end) / 2;
int left = 2 * node + 1;//左子节点的下标
int right = 2 * node + 2;//右子节点的下标
//求出左子节点的值(即从节点left开始,建立范围为a[start]~a[mid])
build(a, tree, left, start, mid);
//求出右子节点的值(即从节点right开始,建立范围为a[start]~a[mid])
build(a, tree, right, mid+1, end);
//当前节点的职位左子节点的值加上右子节点的值
tree[node] = tree[left] + tree[right];
}
}
int main(){
//从根节点(即节点0)开始建树,建树范围为a[0]~a[size-1]
build(a, tree, 0, 0, size-1);
for(int i = 0; i <= 14; i ++)
printf("tree[%d] = %d\n", i, tree[i]);
return 0;
}
运行结果:
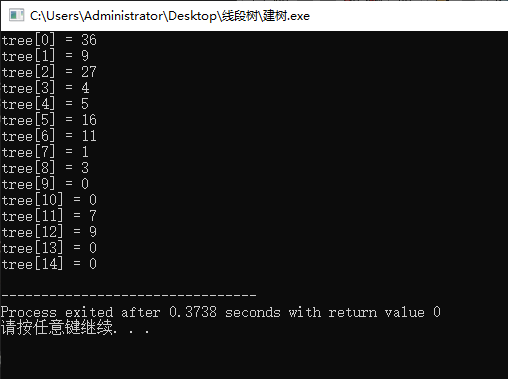
update操作:
- 确定需要改的分支,向下寻找需要修改的节点,再向上修改节点值。
- 与建树的函数相比,update函数增加了两个参数x,val,即把a[x]改为val。
例:把a[x]改为6(代码实现)
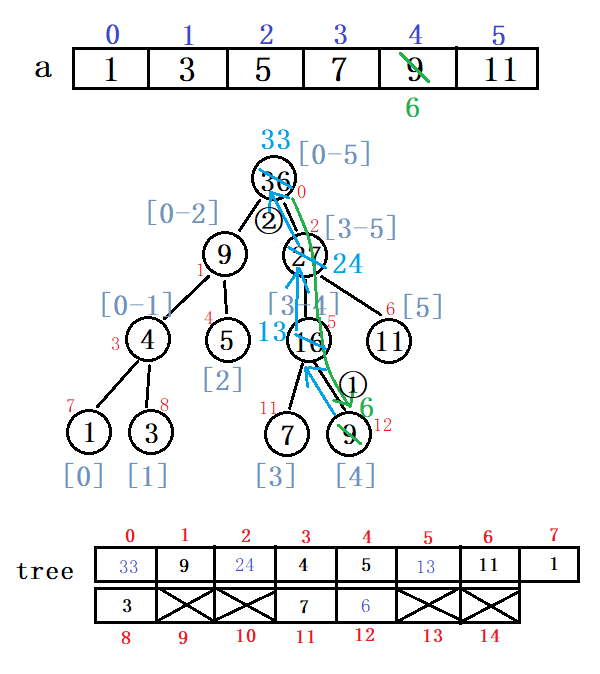
void update(int a[], int tree[], int node, int start, int end, int x, int val){
//找到a[x],修改值
if (start == end){
a[x] = val;
tree[node] = val;
}
else {
int mid = (start + end) / 2;
int left = 2 * node + 1;
int right = 2 * node + 2;
if (x >= start && x <= mid) {//如果x在左分支
update(a, tree, start, mid, x, val);
}
else {//如果x在右分支
update(a, tree, right, mid+1, end, x, val);
}
//向上更新值
tree[node] = tree[left] + tree[right];
}
}
在主函数中调用:
//把a[x]改成6
update(a, tree, 0, 0, size-1, 4, 6);
运行结果:
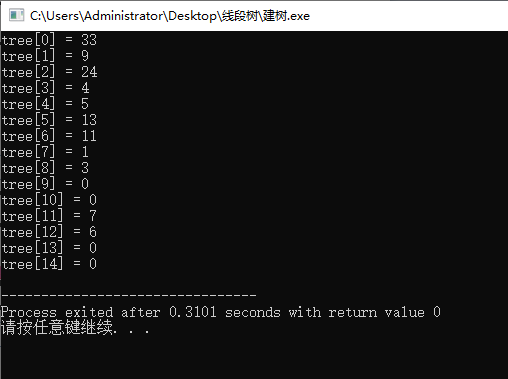
query操作:
- 向下依次寻找包含在目标区间中的区间,并累加。
- 与建树的函数相比,query函数增加了两个参数L,Rl,即把求a的区间[L,R]的和。
例:求a[2]+a[3]+...+a[5]的值(代码实现)
int query(int a[], int tree[], int node, int start, int end, int L,int R){
//若目标区间与当时区间没有重叠,结束递归返回0
if (start > R || end < L){
return 0;
}
//若目标区间包含当时区间,直接返回节点值
else if (L <=start && end <= R){
return tree[node];
}
else {
int mid = (start + end) / 2;
int left = 2 * node + 1;
int right = 2 * node + 2;
//计算左边区间的值
int sum_left = query(a, tree, left, start, mid, L, R);
//计算右边区间的值
int sum_right = query(a, tree, right, mid+1, end, L, R);
//相加即为答案
return sum_left + sum_right;
}
}
在主函数中调用:
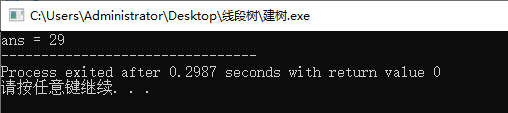
//求区间[2,5]的和
int ans = query(a, tree, 0, 0, size-1, 2, 5);
printf("ans = %d", ans);
运行结果:
最后,献上完整的代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1000;
int a[] = {1, 3, 5, 7, 9, 11};
int size = 6;
int tree[N] = {0};
//建立范围为a[start]~a[end]
void build(int a[], int tree[], int node/*当前节点*/, int start, int end){
//递归边界(即遇到叶子节点时)
if (start == end) {
//直接存储a数组中的值
tree[node] = a[start];
}
else {
//将建立的区间分成两半
int mid = (start + end) / 2;
int left = 2 * node + 1;//左子节点的下标
int right = 2 * node + 2;//右子节点的下标
//求出左子节点的值(即从节点left开始,建立范围为a[start]~a[mid])
build(a, tree, left, start, mid);
//求出右子节点的值(即从节点right开始,建立范围为a[start]~a[mid])
build(a, tree, right, mid+1, end);
//当前节点的职位左子节点的值加上右子节点的值
tree[node] = tree[left] + tree[right];
}
}
void update(int a[], int tree[], int node, int start, int end, int x, int val){
//找到a[x],修改值
if (start == end){
a[x] = val;
tree[node] = val;
}
else {
int mid = (start + end) / 2;
int left = 2 * node + 1;
int right = 2 * node + 2;
if (x >= start && x <= mid) {//如果x在左分支
update(a, tree, left, start, mid, x, val);
}
else {//如果x在右分支
update(a, tree, right, mid+1, end, x, val);
}
//向上更新值
tree[node] = tree[left] + tree[right];
}
}
//求a[L]~a[R]的区间和
int query(int a[], int tree[], int node, int start, int end, int L,int R){
//若目标区间与当时区间没有重叠,结束递归返回0
if (start > R || end < L){
return 0;
}
//若目标区间包含当时区间,直接返回节点值
else if (L <=start && end <= R){
return tree[node];
}
else {
int mid = (start + end) / 2;
int left = 2 * node + 1;
int right = 2 * node + 2;
//计算左边区间的值
int sum_left = query(a, tree, left, start, mid, L, R);
//计算右边区间的值
int sum_right = query(a, tree, right, mid+1, end, L, R);
//相加即为答案
return sum_left + sum_right;
}
}
int main(){
//从根节点(即节点0)开始建树,建树范围为a[0]~a[size-1]
build(a, tree, 0, 0, size-1);
for(int i = 0; i <= 14; i ++)
printf("tree[%d] = %d\n", i, tree[i]);
printf("\n");
//把a[x]改成6
update(a, tree, 0, 0, size-1, 4, 6);
for(int i = 0; i <= 14; i ++)
printf("tree[%d] = %d\n", i, tree[i]);
printf("\n");
//求区间[2,5]的和
int ans = query(a, tree, 0, 0, size-1, 2, 5);
printf("ans = %d", ans);
return 0;
}
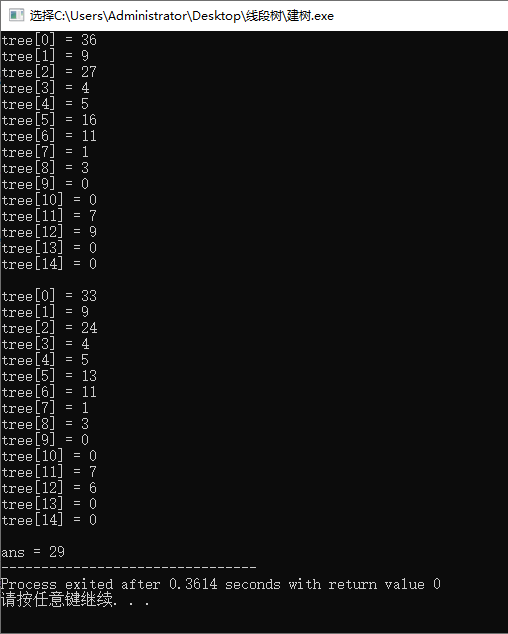
运行结果:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号