03卷积神经网络--入门小案例

01 卷积神经网络理论

注：参考吴恩达老师的课件和下面链接的笔记
参考：https://blog.csdn.net/weixin_36815313/article/details/105731373
1. 卷积运算是卷积神经网络最基本的组成部分，使用边缘检测作为入门样例。

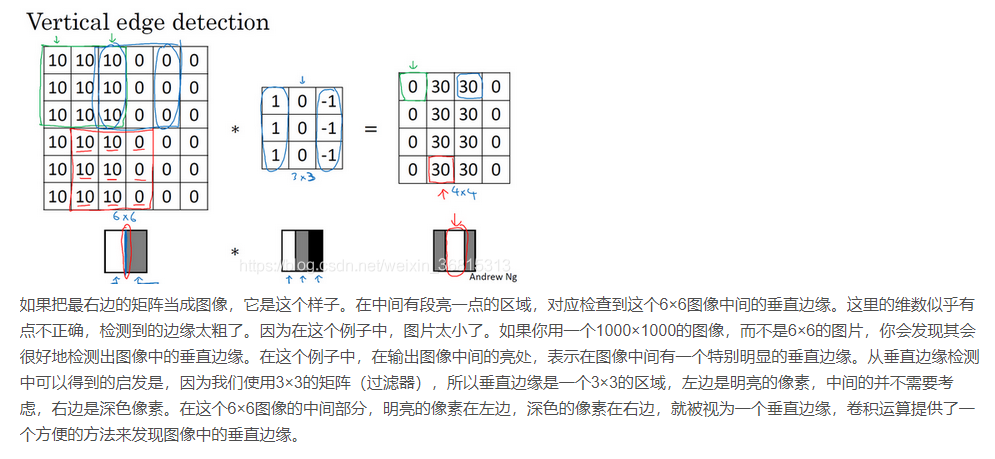
2.为了构建深度神经网络，你需要学会使用的一个基本的卷积操作就是padding，让我们来看看它是如何工作的。
如果我们有一个n∗n的图像，用 f∗f的过滤器做卷积，那么输出的维度就是(n−f +1)∗(n−f+1)。

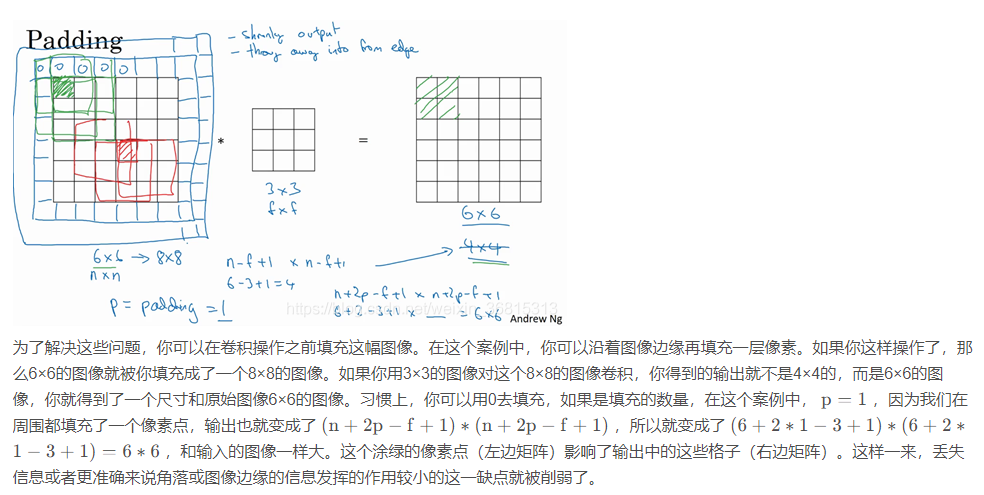
3. 卷积步长
卷积中的步幅是另一个构建卷积神经网络的基本操作。

如果你用一个f∗f的过滤器卷积一个n∗n的图像，你的padding为p，步幅为s ，因为现在你不是一次移动一个步子，而是一次移动s个步子，输出于是变为 \(\frac{n+2p-f}{s}+1 *\frac{n+2p-f}{s}+1\)。
现在只剩下最后的一个细节了，如果商不是一个整数怎么办？在这种情况下，我们向下取整。
4.三维卷积

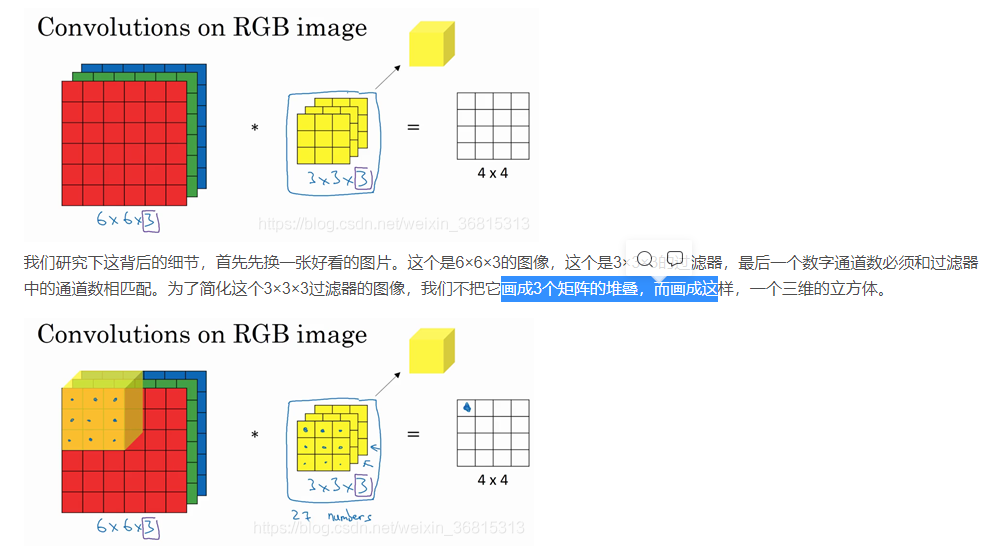
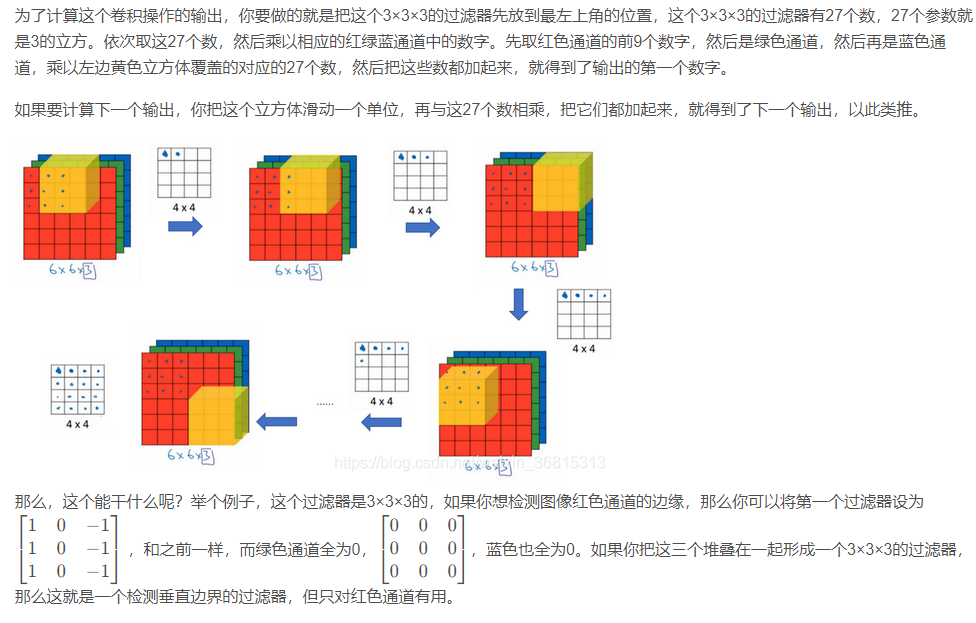
再注意一下这个卷积立方体，一个6×6×6的输入图像卷积上一个3×3×3的过滤器，得到一个4×4的二维输出（三个通道卷积出来的结果相加）。

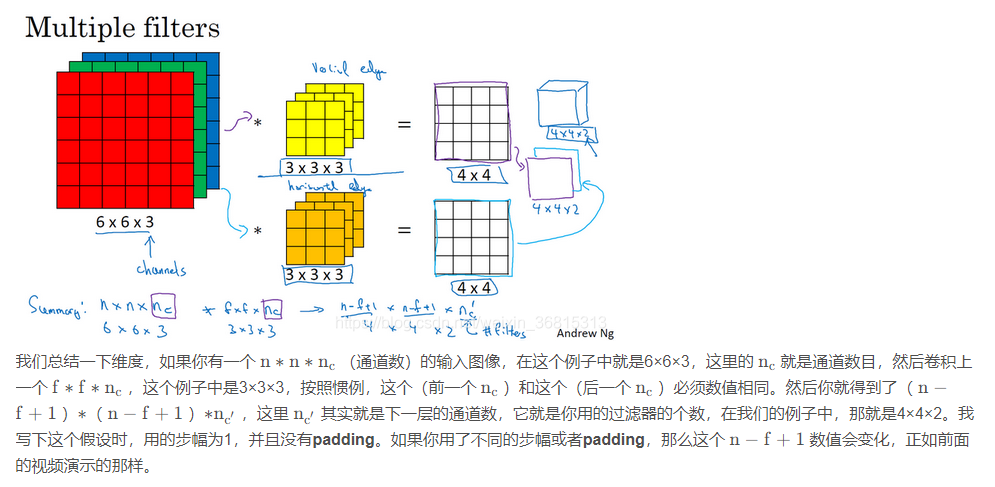
5. 单层卷积网络 (One Layer of a Convolutional Network)

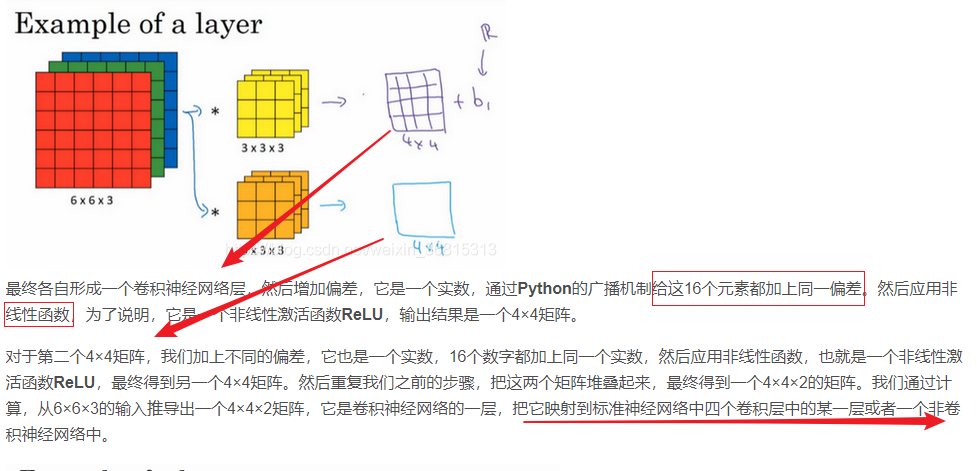
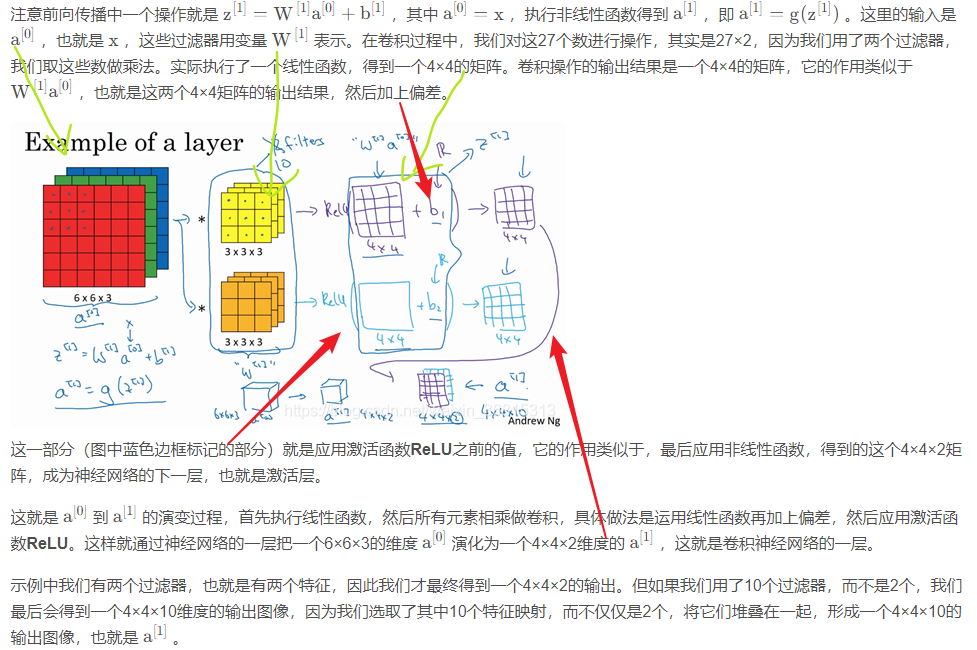
6.池化层 (Pooling Layers)

除了卷积层，卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性，我们来看一下。

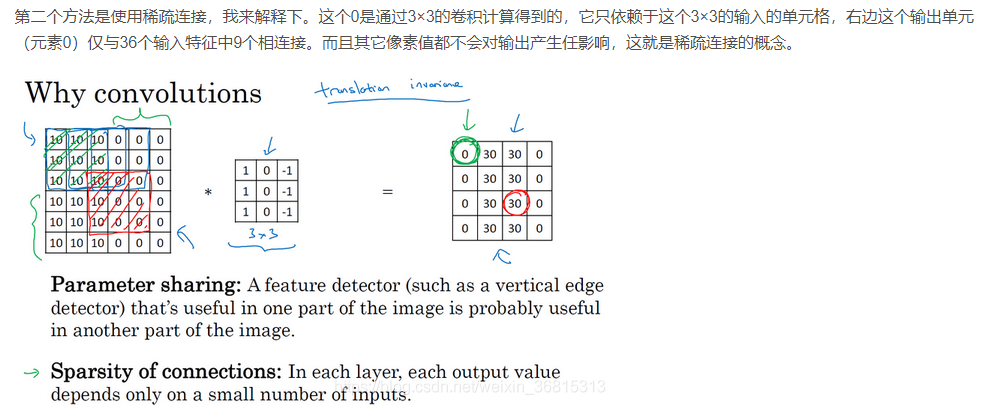
7.为什么使用卷积 (Why Convolutions?)

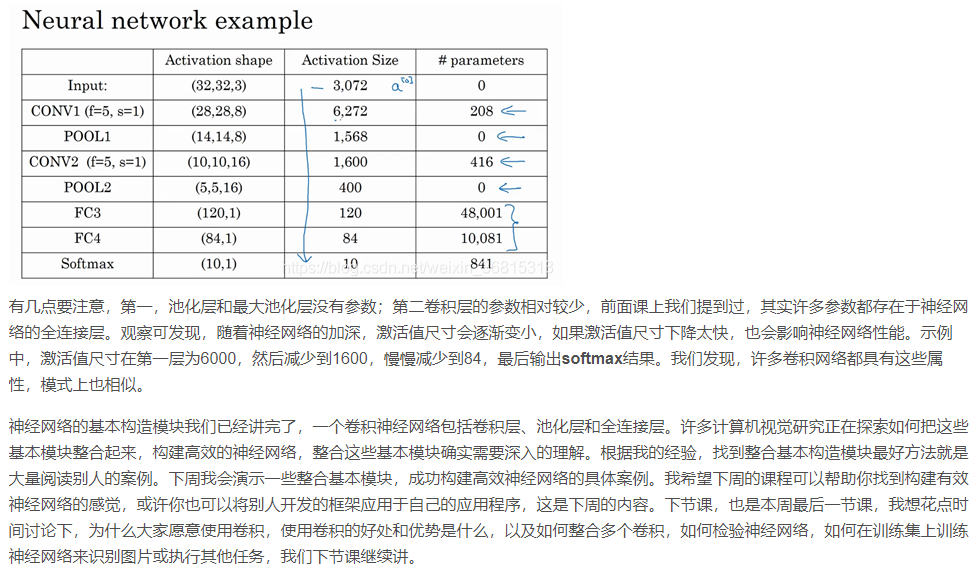
02 pytorch实战

01 任务

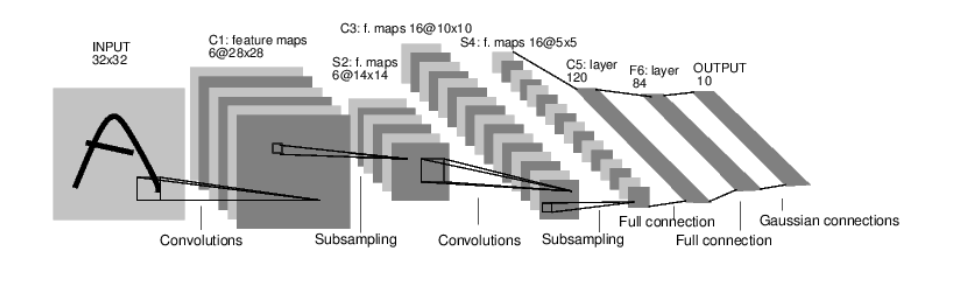
这是一个简单的前馈神经网络，它接收输入，让输入一个接着一个的通过一些层，最后给出输出。
一个典型的神经网络训练过程包括以下几点：
1.定义一个包含可训练参数的神经网络
2.迭代整个输入
3.通过神经网络处理输入
4.计算损失(loss)
5.反向传播梯度到神经网络的参数
6.更新网络的参数，典型的用一个简单的更新方法：weight = weight - learning_rate *gradient

import torch
import torch.nn as nn
import torch.nn.functional as f

class Net(nn.Module):
def init(self):
super().init()
# 1 input image channel, 6 output channels, 5x5 square convolution
# kerne
# 1,1,32,32
self.conv1 = nn.Conv2d(1, 6, 5)
# 1,6,28,28
# 1,6,14,14
self.conv2 = nn.Conv2d(6, 16, 5)
# 16,24,24
# an addine opration: y=wx+b
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = f.relu(self.conv1(x))
x = f.max_pool2d(x, (2, 2))
# If the size is a square you can only specify a single numbe
x = f.max_pool2d(f.relu(self.conv2(x)), 2)
x = x.view(-1,len(x.flatten()))
x = f.relu(self.fc1(x))
x = f.relu(self.fc2(x))
x = self.fc3(x)
return x

if name == 'main':
net = Net()
a = torch.randn(1, 1, 32, 32)
out = net(a)
print(out)
# tensor([[ 0.0361, 0.0082, -0.0659, 0.0686, -0.1300, 0.0308, -0.0280, 0.0833,
# 0.1442, -0.0974]], grad_fn=)

print(net)
# Net(
#   (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
#   (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
#   (fc1): Linear(in_features=400, out_features=120, bias=True)
#   (fc2): Linear(in_features=120, out_features=84, bias=True)
#   (fc3): Linear(in_features=84, out_features=10, bias=True)
# )
params = net.parameters()
for i in params:
    print(i.shape)
# torch.Size([6, 1, 5, 5])
# torch.Size([6])
# torch.Size([16, 6, 5, 5])
# torch.Size([16])
# torch.Size([120, 400])
# torch.Size([120])
# torch.Size([84, 120])
# torch.Size([84])
# torch.Size([10, 84])
# torch.Size([10])

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as f
torch.manual_seed(10)

class Net(nn.Module):
    def __init__(self):
        super().__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kerne
        # 1,1,32,32
        self.conv1 = nn.Conv2d(1, 6, 5)
        # 1,6,28,28
        # 1,6,14,14
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 16,24,24
        # an addine opration: y=wx+b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = f.relu(self.conv1(x))

        x = f.max_pool2d(x, (2, 2))

        # If the size is a square you can only specify a single numbe
        x = f.max_pool2d(f.relu(self.conv2(x)), 2)

        x = x.view(-1,len(x.flatten()))
        x = f.relu(self.fc1(x))
        x = f.relu(self.fc2(x))
        x = self.fc3(x)
        return x


if __name__ == '__main__':
    net = Net()
    a = torch.randn(1, 1, 32, 32)
    target = torch.randn(10)
    target = target.view(1, -1)
    criterion = nn.MSELoss()
    optimizer = optim.SGD(net.parameters(), lr=0.01)
    for i in range(100):
        optimizer.zero_grad()
        out = net(a)
        loss = criterion(out, target)
        loss.backward()
        optimizer.step()
        print(loss)