BUAA OO 第一单元总结
前言
本文将按照作业的顺序依次展示作业中的思路,以及个人认为比较有价值的代码。考虑到阅读体验,本文将圈复杂度分析放在了文末。
第一次作业
结构概述
类图如下

整个表达式的处理流程大致如下图

空白符的处理
空白符在一开始直接删去即可。
String s = string.replaceAll("[ \\t]", "");
这一方法将延续三次作业
简化方式
化简
化简这一步的示意图如下:
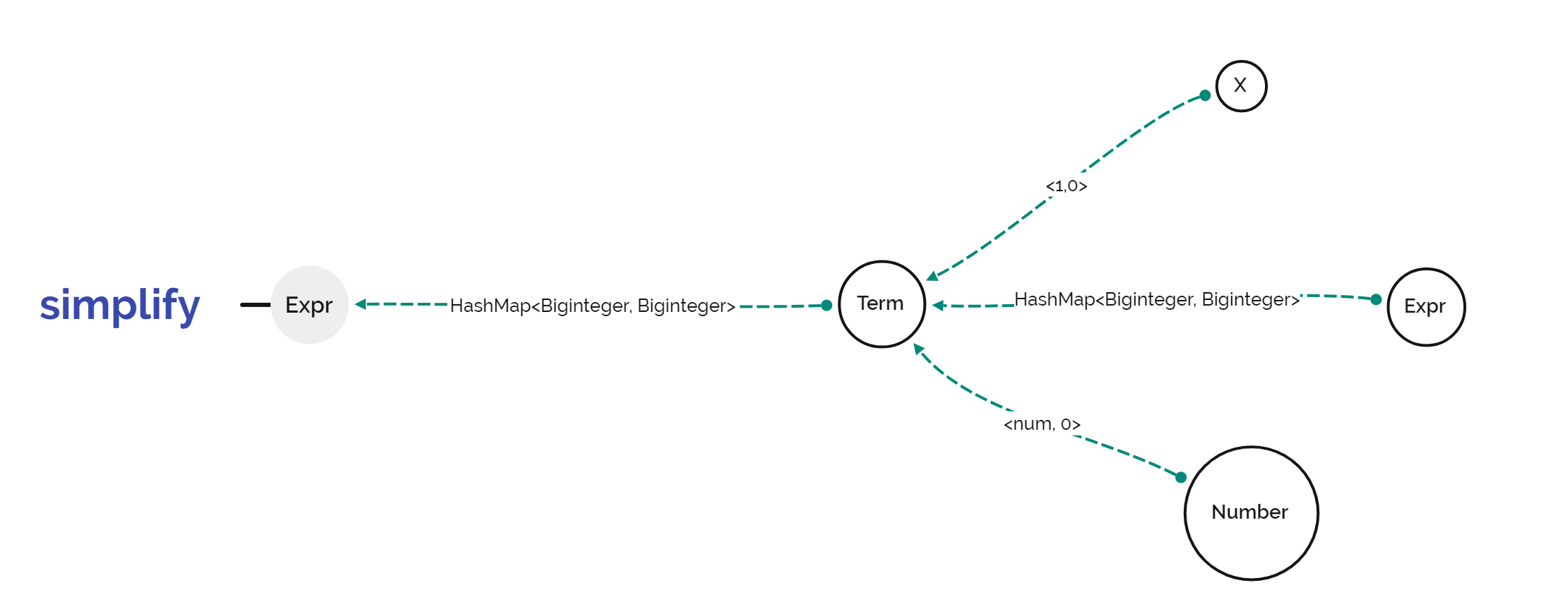
在expr.simplify()这一步中,因子只能是x或常数,因此,在简化时,只需要递归地向上传一个HashMap<Biginteger, Biginteger>,在term.simplify()中,完成HashMap<Biginteger, Biginteger>之间相乘,在expr.simplify()中完成HashMap<Biginteger, Biginteger>的相加即可。其中,前面的Biginteger代表指数,后面的Biginteger代表系数。
符号处理
观察表达式的形式化表述:
表达式 → 空白项 [加减 空白项] 项 空白项 | 表达式 加减 空白项 项 空白项
项 → [加减 空白项] 因子 | 项 空白项 * 空白项 因子
可以发现,如果不考虑数量,所有的加减号理论上都可以认为是项(Term)前面的符号。因此,在符号处理上,在表达式处理流程的parseExpr()这一步中,符号将交由Parser中的parseTerm()方法开头处统一处理。
而带符号的整数中,发现Biginteger(string)的方法,可以处理string前的正负号,因此直接用这一函数处理。
这一处理方法将会延续整个第一单元。
性能优化
- 将
x**2替换为x*x可以减少一个字符。处理方法为:在printRes()这一步中,对即将打印的x**2进行特判,并进行替换即可。 -x+1这样负号在前的表达式,可换为1-x从而减小长度。处理方法为:遍历HashMap<Biginteger, Biginteger>的所有元素,找到系数为正数的项提前打印并删除,再将这个HashMap进行一般流程的打印。
第二次作业
类图如下
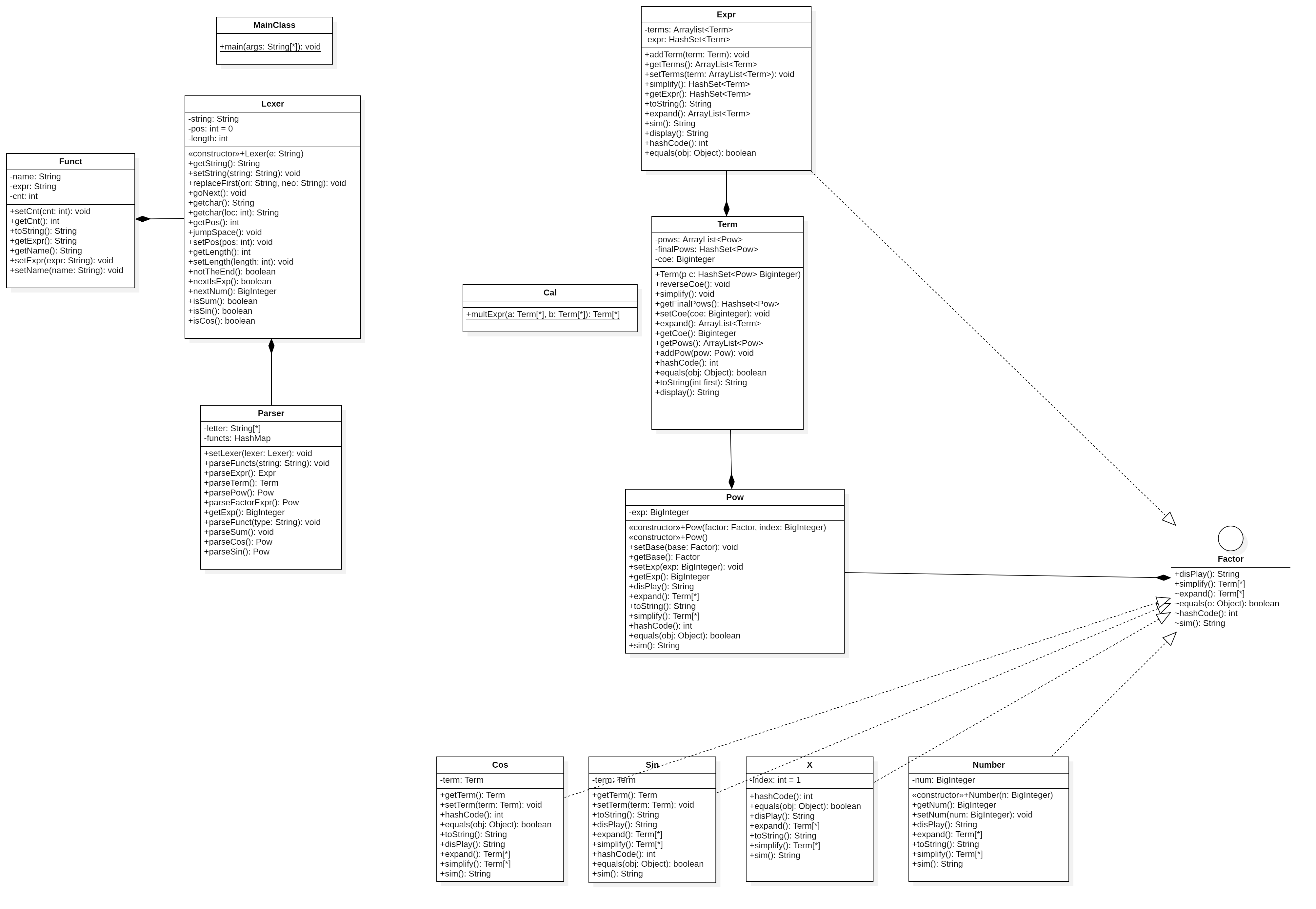
表达式的整个处理流程大致如下图

本次作业中,将第一次作业的表达式层次:Expr-Term-Factor改为Expr-Term-Pow-Factor。
自定义函数
笔者对自定义函数的处理方式为字符串替换。字符串需要解决如下的问题:
字符串替换不当导致语义变化
笔者的解决方法是:能加括号的地方尽可能加括号。
由于采用层次化的方法解析表达式,因此再深的括号,这个程序架构都能够充分展开,因此,能加括号的地方尽可能加括号并不会带来错误。
形参为x时,替换可能出bug
对于自定义函数,由于自定义函数中的参数x、y、z出现的顺序不固定,且形参复用了自变量x这一字母。于是,如果直接进行字符串的替换,会误将自变量x当作形参x进行替换而出错。
对此,笔者的方法是:在parseFunct()这一步,将自定义函数的参数依次换为p、q、l这三个在整个流程中未使用的字母,这样就不用担心字符串替换时出错了。而后续替换,也将每一个形参替换为传入的参数。
private String[] letter = { "l", "q", "p" };
而参数的匹配,采用的是正则表达式匹配。
switch (funct.getCnt()) {
case 1:
pattern = "[fgh]\\((.*)\\)$";
break;
case 2:
pattern = "[fgh]\\((.*),(.*)\\)$";
break;
case 3:
pattern = "[fgh]\\((.*),(.*),(.*)\\)$";
break;
default:
break;
}
Pattern tmp = Pattern.compile(pattern);
Matcher matcher = tmp.matcher(ori);
if (matcher.find()) {
for (int i = 0; i < funct.getCnt(); i++) {
functString = functString.replaceAll(letter[i], "(" + matcher.group(1 + i) + ")");
// not sure
}
}
求和函数
求和函数的处理同样是利用正则表达式匹配,并替换字符串。唯独需要注意的是,sin函数中也有“i”字符,进行替换的时候要当心不要将其换为常数。方法如下:
String termString = exp.replaceAll("(?<!s)i", "(" + i + ")");
计算顺序的问题
由于设计展开括号的时候,
简化方式
本次简化分为两步:展开括号(expand),进行合并(simplify)。
expand
流程示意图如下:
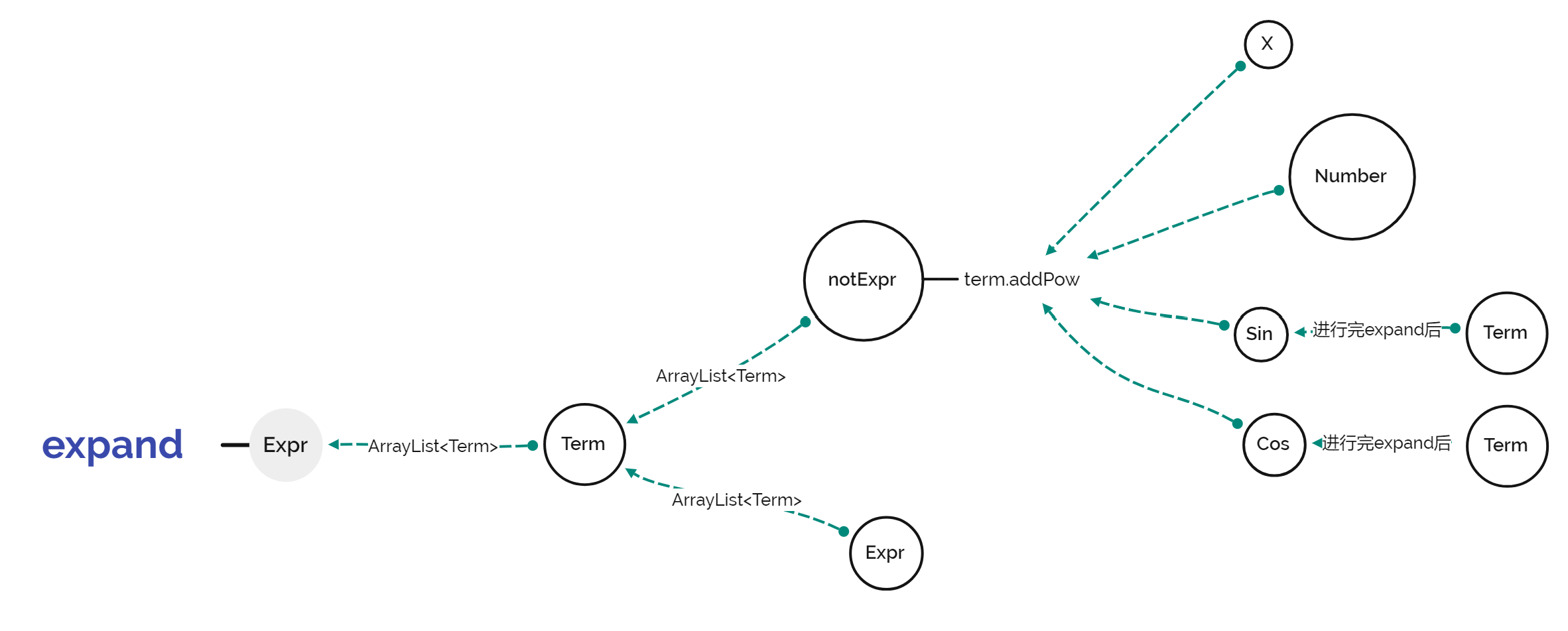
由于因子不再是只有数字和x了,因此向上传递HashMap不再行得通。因此,采用向上传递ArrayList<Term>的方式进行括号的展开。
simplify
对项,需要将Pow类底数base相同的因子合并,且指数相加。
对表达式,需要识别除系数外相同的项term,并将其系数coe相加。
此时,考虑采用重写HashCode()和equals()方法,并利用HashSet<>的元素不可重复性。
大致的流程为:
在项中:将ArrayList<Pow>的每个元素逐一放入HashMap<Factor, BigInteger>中,若Factor为数字,则乘入系数coe中;若出现相同的Factor,则指数改为两者指数之和。最后删去指数为0的对。
在表达式中:将ArrayList<Term>的每个元素逐一放入HashMap<HashSet<Pow>,BigInteger>中,其中value为系数coe。若出现相同的HashSet<Pow>,则系数改为两者系数之和。最后删去系数为0的对。
由于化简之前已经进行了括号的展开expand,故不会出现x和(x)无法被认为相等的情况。(因为此时根本不会出现(x))。
性能优化
奇偶优化
由于cos、sin函数具有奇偶性,因此,无脑将cos、sin中的符号提出,至少是不会增加结果的长度的。
实现方法为:在simplify()这一步中,判断一下三角函数内因子的符号,如果为负,则改为正,并向外传递一个信号,Term类接到这个信号后,系数*-1即可。
三角函数原点的值
将sin(0)换为0,cos(0)换为1可以缩短结果长度。方法为:在simplify()这一步时,对三角函数里面的内容进行判断。若为0,则将Pow的底数base替换为数字类Number,其值与原三角函数相同。
答案输出
第二次作业中,答案字符串的复杂度要远远高于第一次作业,如果和第一次作业一样,在main函数写printRes()方法,那么这一方法的长度必然会超标。因此,本次作业改为采用在各个层次各自递归下降地toString()方法,并进行拼合。
由于数据限制,sin、cos中的Term在输出答案时,x**2不能被替换为x*x,故为sin、cos中的Term定制了一个转为字符串的方法display(),以满足题目要求。
出现的bug
- 由于之前一直采用
Biginteger(string)的方式处理常数,可省去特判数字前的符号这一步骤。因此疏忽了数字前面可能会出现"+"。故并没有在匹配求和函数上下限时考虑数字前的“+”,导致正则表达式匹配求和函数时匹配失败。解决方法为:修正正则表达式,使其可以匹配"+"。 - 在奇偶优化时,未考虑三角函数的指数为偶数时,Term不应该*-1,导致出bug。解决方法为:将“如果为负,则改为正,并向外传递一个信号”改为“如果为负,则改为正,若三角函数指数为奇数,则向外传递一个信号”。
- 未进行深拷贝,导致项与项相乘时出错。
第三次作业
类图如下
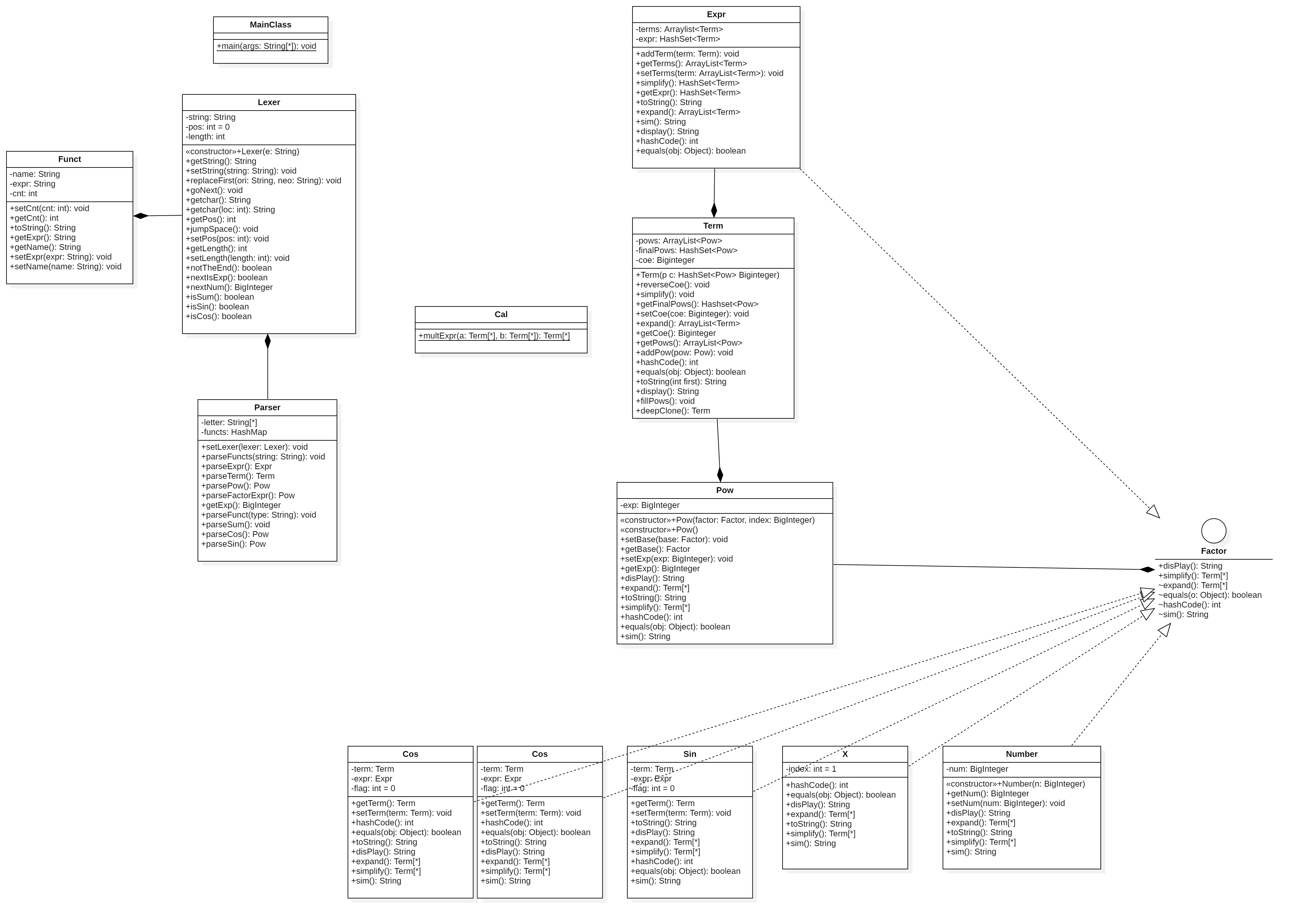
表达式的整个处理流程大致如下图

三角函数的处理
由于三角函数中的因子限制放宽,因此在三角函数的化简过程有较大变化。三角函数sin、cos中的内容由常数或幂函数变为了一般的因子。笔者选择了直接按照表达式处理。
为了能充分复用第二次作业的代码,本次作业虽然将三角函数内的因子按表达式处理,但在expand这一步提前对三角函数内的表达式进行了expr.simplify(),并进行判断:若Expr只有唯一的项,且项的结果相当于常数或幂函数(即不需要加括号),则将表达式中唯一的项复制到Sin、Cos类里面的Term类属性中,并在toString的步骤中,按第二次作业的方法处理。反之,保留这个Expr类变量,在toString的步骤中,按表达式处理。
这里展示toString()方法的代码:
public String toString() {
if (flag == 0) {
if (term.getFinalPows().isEmpty()) {
return "cos(" + term.display() + ")";
}
if (term.getPows().get(0).getBase() instanceof X
&& term.getPows().get(0).getExp().equals(BigInteger.valueOf(2))) {
return "cos(" + "x**2" + ")";
} else {
return "cos(" + term.display() + ")";
}
} else {
return "cos((" + expr.toString() + "))";
}
}
简化方式
简化分为两步:展开括号(expand),进行合并(simplify)。
expand
示意图如下:

大部分与第二次作业一致,除了三角函数类里增加了Expr类指令,并在expand的步骤中提前进行了simplify这一步。
simplify
同作业二。
性能优化
本次作业未做额外的优化,优化方式同作业二。
求和函数的参数替换
由于此时数据限制放宽,之前使用正则表达式提取参数将无法应对如f(sum(i,1,2,(x)**2),((((x)))))这样刁钻的数据。此时,考虑通过括号堆栈的方式,找到每一个逗号间隔内的内容。代码如下:
groupBegin[0] = start + 2;
Funct funct = functs.get(type);
while (num != 0) {
String now = lexer.getchar(end);
if (now.equals("(")) {
num++;
} else if (now.equals(")")) {
num--;
}
if (now.equals(",") && num == 1) {
groupEnd[k] = end;
k++;
groupBegin[k] = end + 1;
}
end++;
}
groupEnd[k] = end - 1;
出现的bug
- 版本迭代的时候没有注意到求和函数
sum的求和上限与下限并没有明确的大小限制,因此在写的时候用int型的变量去装上下限了。爆栈的数据在第二、三次作业的中、强测中均未出现,因此并没有修改这一bug,而在互测环节被hack了。
圈复杂度分析
第一次作业


第二次作业
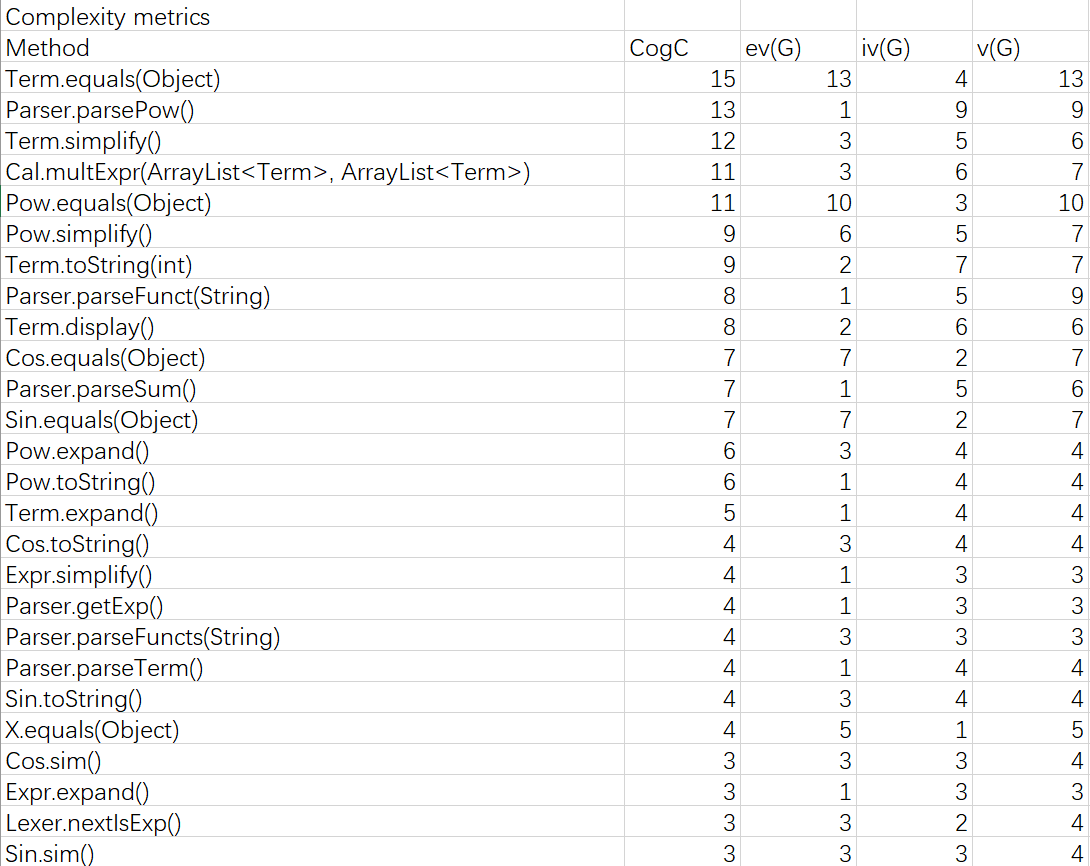
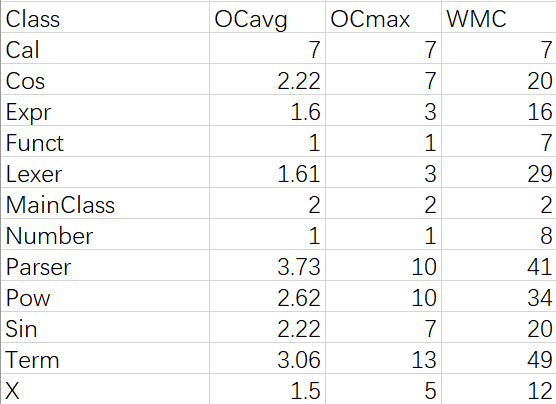
由于Cal类中的方法,只在Term类中被使用。因此,如果将Cal中的方法直接写在Term里面,就可以少一个类,可以降低圈复杂度。
第三次作业
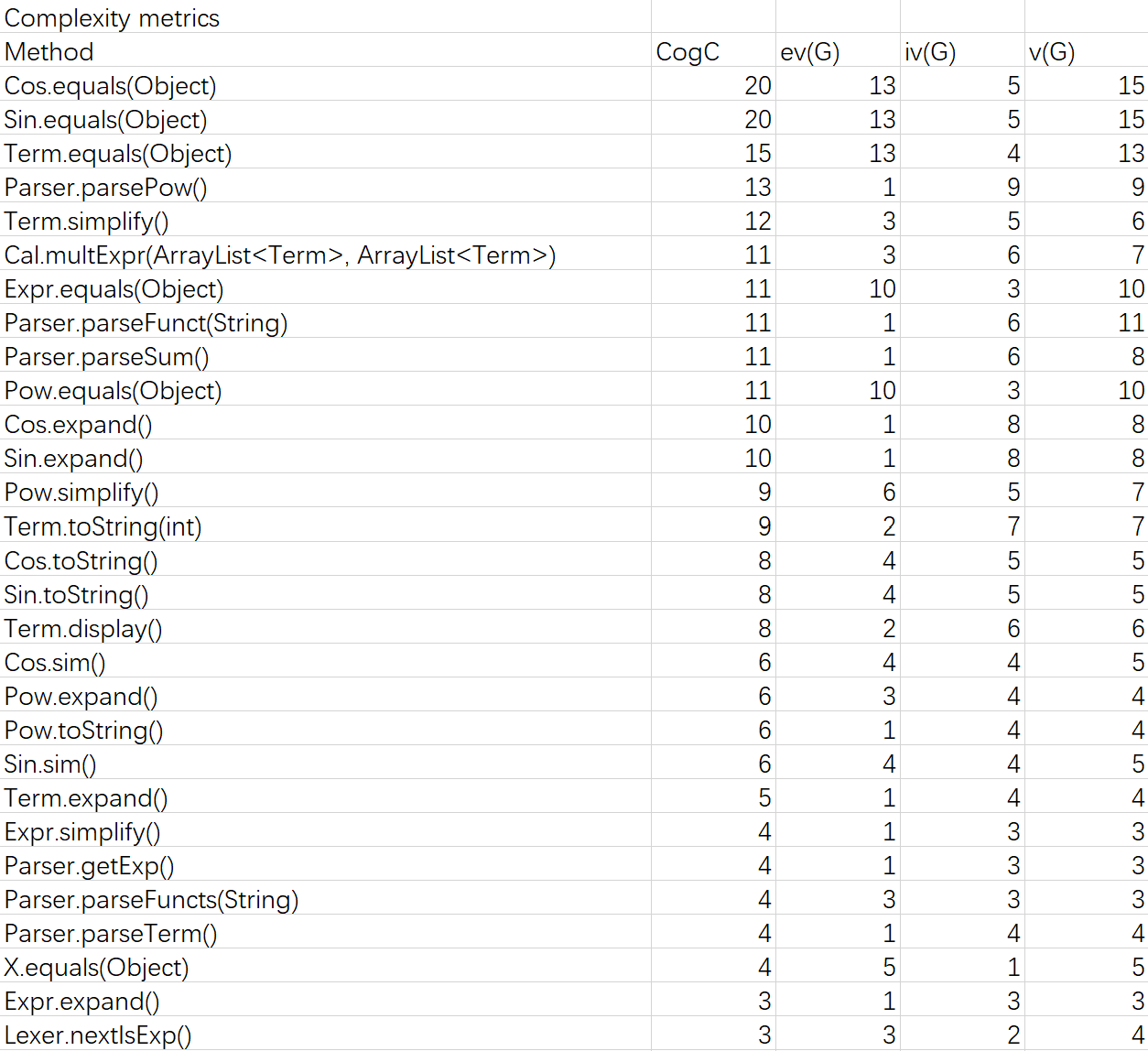
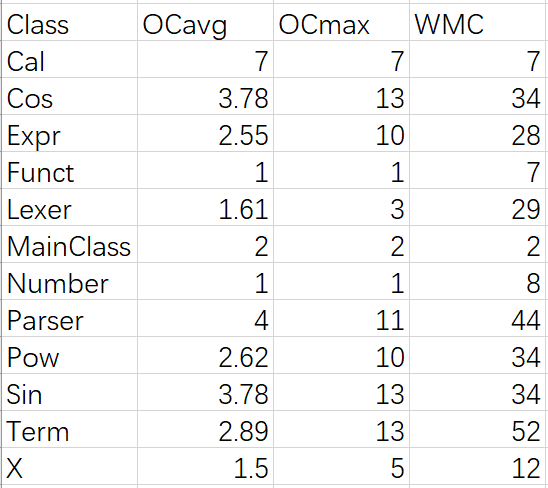
equals函数的圈复杂度这么高,好像也是没有办法。
这个阶段的作业由于不敢将原来的方法改写,想要实现新的功能时,就会重写一个方法,增加一些不必要的属性。可能这就是屎山的诞生吧。
hack思路
- 常数: 考虑前导零和正负号的处理是否正确
- 幂函数:考虑零次方的结果是否恒为1,考虑项的合并是否正确。考虑偶次幂消去负号的这一步是否正确。
- 求和函数:考虑求和上下限是否支持正负,是否支持上限小于上限。考虑正负号的代入是否正确。
- 三角函数:考虑三角优化是否正确,考虑正负号的优化是否正确,考虑多层三角函数嵌套是否支持。
- 自定义函数:考虑参数的替换是否正确,考虑形参的顺序是否会干扰代入。
感想
第一周的OO大主题为表达式的解析,整个作业的走向基本是可以预见到的。但是在实际书写的过程中,还是无法在一开始就想好以后的通用度问题,数据的覆盖面上,也比较依赖评测机。比如第二次作业相第三次作业迭代的时候,原以为第二次作业做的一些超前的工作,可以直接应付第三次作业,但是在开放中测后还是发现了很多问题,重写了不少代码。这一点可能还是个人能力不足。
以及,个人也曾立志要好好写一个数据生成程序和自动评测程序,但最后还是没写,白嫖了讨论区……
总体上还是有收获的吧,也有一些遗憾,希望以后能写得更好。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号