快慢指针和链表

快慢指针和链表的环

相信用快慢指针确定链表是否有环大家并不陌生，但是如何确定这个链表环起点的位置是一个问题。

为了深入了解，我画了个图方便理解。

下图表示了快慢指针的流程，现在假设（有环）：

快慢指针都从起点B开始，快慢指针最终相交于点C，环的起点位于S。

我们假设慢指针走了 k 的距离，那么快指针走了 2k 的距离，其中(0<k<2k<n)，设 SC 的距离为m，注意是顺时针（S到C）的距离，那么：

 

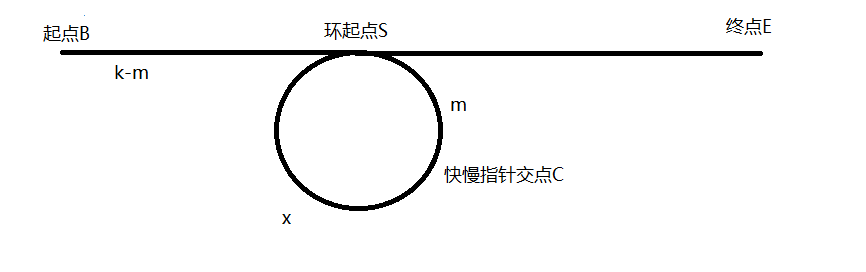
 可知，BS的距离为 k-m，我们现在 CS 的距离未知，我们假设其为 x，现在来求解x

我们知道快指针走了 2k 的距离是吧，也就是 BS + SC + CS +SC = 2k

那么， k-m + m + x + m = 2k;　　可知 x = k-m，好像发现了不得了的事情！！！，CS和BS距离是一样的！！！

我们通过快慢指针确定了交点C后，只要让快指针指向B，速度设置为和慢指针一样为1，让慢指针从C开始，一起走，只要他们相遇，就一定是在环起点S相遇。CS = BS = k-m

 

因此，快慢指针确定环起点的结论就是，让快指针变成慢指针从起点开始，让慢指针从交点开始，一起走，相遇的点就是环的起点。

快慢指针和中位数

 用快慢指针确定中位数原理很简单，同样是让快指针速度为2，慢指针速度为1，当快指针走到头时，慢指针就会留在中位数的地方。

奇数长度情况：

0　　1　　2　　3　　4　　5　　6

快指针3次结束，慢指针3次停留在 3 上面，正好是中位数，完全正确

偶数长度情况：

0　　1　　2　　3　　4　　5

快指针3次结束，慢指针3次停留在3上面，位于中间偏右位置，想要停留在中间偏左位置的话：当快指针走不足两格位置时，不算该次数，那么快指针走2次，慢指针走2次停在 2 上面。

 

快慢指针和倒数第K个数

用快慢指针得到倒数第K个数非常简单，一次遍历即可。

0　　1　　2　　3　　4　　5　　6　　7

求倒数第 k 时，我们让快慢指针速度都为1，让快指针先走 k 步 后再同步走，这样当快指针到头的时候，慢指针正好停留在倒数第k个位置上面。