神经网络1

常见激活函数

Sigmoid

sigmoid非线性函数的数学公式是，函数图像如上图的左边所示。在前一节中已经提到过，它输入实数值并将其“挤压”到0到1范围内。更具体地说，很大的负数变成0，很大的正数变成1。

缺点

Sigmoid饱和使梯度消失

神经元的激活在接近0或1处时会饱和，在这些地方梯度可能为0

sigmoid的输出不是零中心的

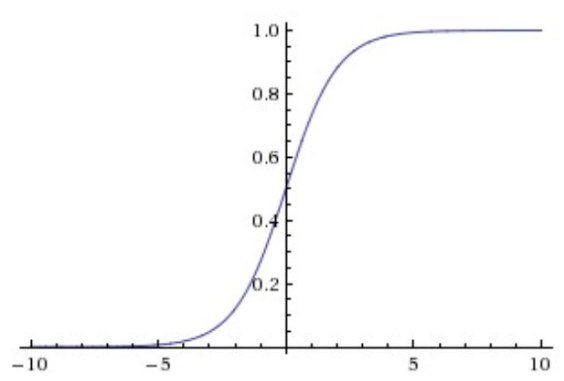
上图是Sigmoid的图像

这种情况（不是零中心），在一定程度上影响了梯度下降，使梯度下降速度变慢

参考博客

 

tanh

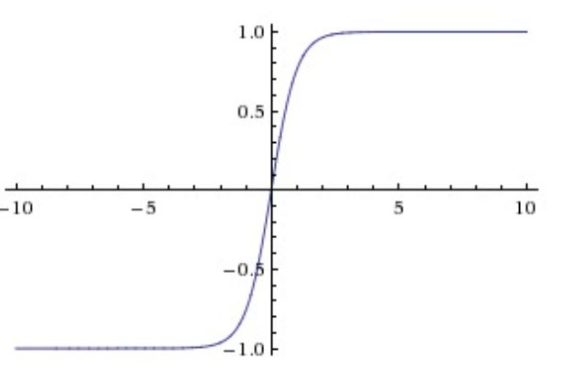
这个函数将数值压缩到-1~1之间，和Sigmoid函数一样，他也存在饱和情况，但是tan是零中心的

注意tanh神经元是一个简单放大的sigmoid神经元，具体说来就是：。

 

ReLu

函数公式是，就是一个关于0的阈值

优点

对于前两种来说，ReLu对于随机梯度下降具有巨大的加速作用（有论文指出有6倍之多）

sigmoid和tanh含有指数运算等操作，会耗费居多的运算资源，而ReLu不会

缺点

在训练的时候，ReLU单元比较脆弱并且可能“死掉”

举例来说，当一个很大的梯度流过ReLU的神经元的时候，可能会导致梯度更新到一种特别的状态，在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生，那么从此所以流过这个神经元的梯度将都变成0。也就是说，这个ReLU单元在训练中将不可逆转的死亡，因为这导致了数据多样化的丢失。例如，如果学习率设置得太高，可能会发现网络中40%的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。通过合理设置学习率（步长），这种情况的发生概率会降低。

 

Leaky ReLU

Leaky ReLU 是为了解决 ReLU 死亡而做的尝试

ReLU中当x<0时，函数值为0。而Leaky ReLU则是给出一个很小的负数梯度值，比如0.01。所以其函数公式为其中是一个小的常量。

 

Maxout

Maxout是对ReLU和leaky ReLU的一般化归纳，它的函数是：

Maxout神经元就拥有ReLU单元的所有优点（线性操作和不饱和），而没有它的缺点（死亡的ReLU单元）

然而和ReLU对比，它每个神经元的参数数量增加了一倍，这就导致整体参数的数量激增。

 

总结

用ReLU非线性函数。注意设置好学习率，或许可以监控你的网络中死亡的神经元占的比例。

如果更考虑死亡率那么就尝试 Leaky ReLU 和 Maxout  ，不要用 sigmoid，

不过可以尝试 tanh， 效果应该没有 Leaky ReLU 和 Maxout 好

 

神经网络结构

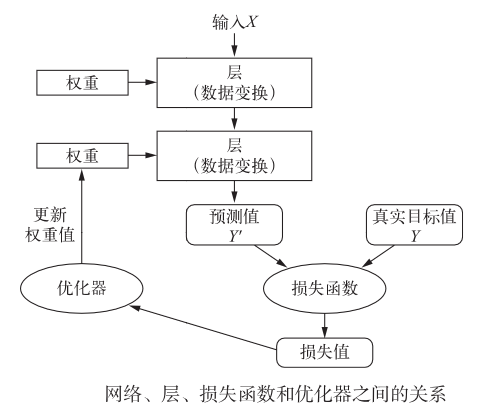
图片来自（python深度学习）

神经网络被建模成神经元的集合，神经元之间以无环图的形式进行连接。

一些神经元的输出是另一些神经元的输入，在网络种不允许有循环（也就是环）

有环可能导致前向传播在神经元里转圈圈

 

层

通常神经网络模型中神经元是分层的

对于普通神经网络，最普通的层类型是全连接层，

全连接层

全连接层中的神经元与其前后两层的神经元是完全成对连接的，但是在同一个全连接层内的神经元之间没有连接

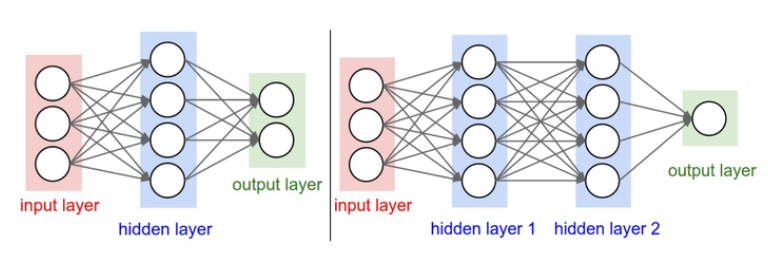
层与层间神经元是全连接，层内神经元是不连接的

全连接层的前向传播一般就是先进行一个矩阵乘法，然后加上偏置并运用激活函数

理解全连接层的神经网络

可以认为它们定义了一个由一系列函数组成的函数族，网络的权重就是每个函数的参数。

现在看来，拥有至少一个隐层的神经网络是一个通用的近似器。

给出任意连续函数和任意，均存在一个至少含1个隐层的神经网络

（并且网络中有合理选择的非线性激活函数，比如sigmoid），对于，使得。

换句话说，神经网络可以近似任何连续函数

问题：一个隐层就能近似任何函数，那为什么还要构建更多层来将网络做得更深？

虽然一个2层网络在数学理论上能完美地近似所有连续函数，但在实际操作中效果相对较差。

理论上深层网络（使用了多个隐层）和单层网络的表达能力是一样的，但是就实践经验而言，深度网络效果比单层网络好。

 

输出层

由于输出层大多用于表示分类的评分值，因此是任意值的实数，或者说某种实数的目标数（比如：回归）

输出层一般不具有激活函数，或者说他只有应该线性相等函数。

 

神经网络的命名

n层神经网络，实际上是n+1 层， 没有把输出层

单层神经网络就是没有隐含层，即输入直接到输出

 

神经网络的尺寸

度量神经网络的尺寸主要有两个：神经元个数，另一个是参数个数  

• 第一个网络有4+2=6个神经元（输入层不算），[3x4]+[4x2]=20个权重，还有4+2=6个偏置，共26个可学习的参数。
• 第二个网络有4+4+1=9个神经元，[3x4]+[4x4]+[4x1]=32个权重，4+4+1=9个偏置，共41个可学习的参数。

 

为了方便对比，现代卷积神经网络能包含约1亿个参数，可由10-20层构成（这就是深度学习）。

 

设置层的数量和尺寸

增加层的数量和尺寸（单层神经元个数）时，网络的容量上升了。

神经元们可以合作表达许多复杂函数，所以表达函数的空间增加。

更多神经元的神经网络可以表达更复杂的函数。然而这既是优势也是不足，

优势是可以分类更复杂的数据，不足是可能造成对训练数据的过拟合。

防止神经网络的过拟合有很多方法（L2正则化，dropout和输入噪音等），这些方法比单纯减少神经元个数要好

 

不要减少网络神经元数目的主要原因在于小网络更难使用梯度下降等局部方法来进行训练：虽然小型网络的损失函数的局部极小值更少，也比较容易收敛到这些局部极小值，但是这些最小值一般都很差，损失值很高。相反，大网络拥有更多的局部极小值，但就实际损失值来看，这些局部极小值表现更好，损失更小。