K——最近邻算法（KNN）

两种距离

曼哈顿距离和欧式距离

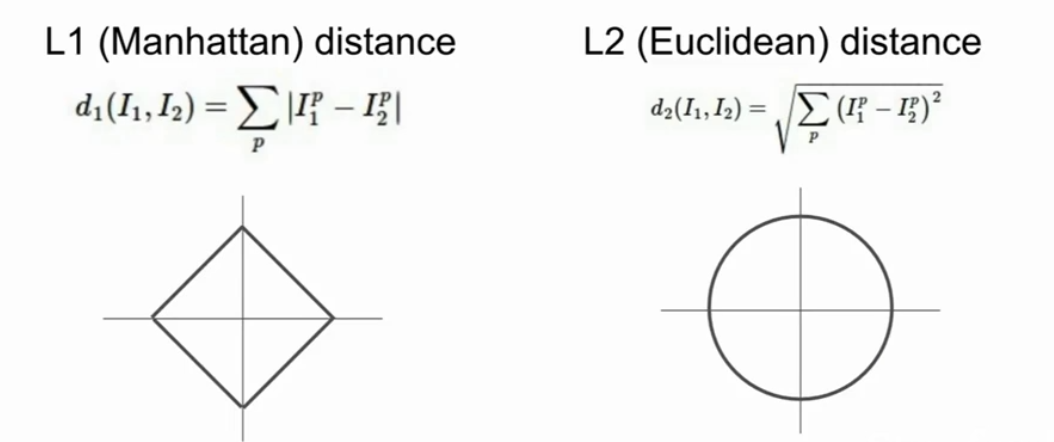
曼哈顿距离 :  L1取决选择的坐标系统，旋转坐标系会造成改变L1 

欧式距离： L2不会

 

如果输入的特征向量，如果向量的一些值由特殊含义L1 可能会合适一点

如果是一个通用向量，不知道其中的元素意义，那么L2会好一点

 

通过使用不同的距离，Knn可以泛化到不同的数据类型，可以是数据，图像，文本，甚至视频等

唯一不同的就是需要指定一个距离函数

 

在使用这个算法是我们需要考虑的是超参数（K值和不同的距离度量 ）

超参数的选择不能通过训练得到，原则上k值越大结果越准确，但是实际上一般取20以内

 

那么在什么情况下L1比L2表现的更好

L1依赖数据坐标系统

但总体上就是根据实际问题来决定，可以两个都尝试看哪个效果更好，也就是哪个的准确率更高

我们关心的不是尽可能拟合训练集，而是对未知对象的分类

切记根据测试集来选择尽可能的完美超参数，这可能只是在这个测试集最好的超参数

一般的做法

将数据分为三部分训练集，验证集，测试集

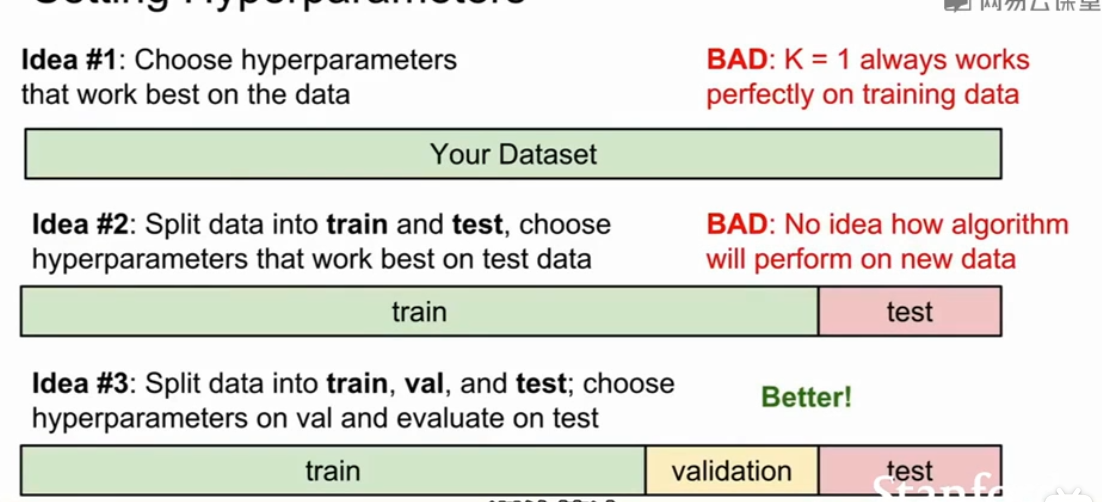
在训练集上训练在验证集上评估，并选出最佳参数，

然后在测试集上跑一跑（此时才能反映你的超参在未知数据的表现）

 

另一个做法——交叉验证

在小数据集中常用，在深度学习中不常用

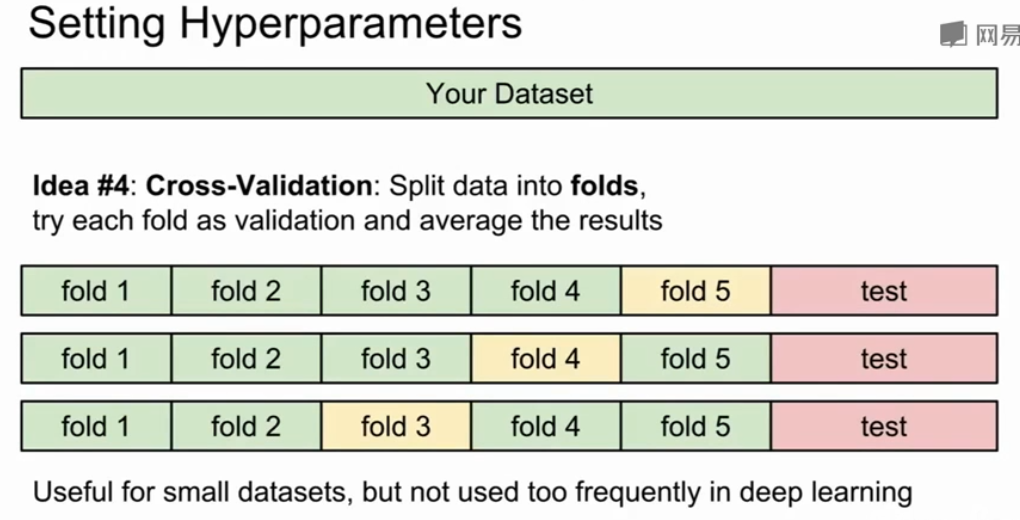
将测试分为很多份，将每个份都作最新的验证集

1，2，3，4 训练， 5验证

然后 1，2，3，5训练 4验证

……

看哪组超参数表现比较好，但这种方式很耗费算力

划分测试集的不能按照收集的时间，应该随机

 

但是L1和L2不太适合区分图像的相似度

 

维度灾难