A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms

介绍

多视图立体(MVS)重建算法是指一组用于从多个场景或物体的二维图像中重建三维(3D)模型的算法。这些算法旨在通过在不同视图中建立点或特征之间的对应关系来恢复场景的几何形状和外观。
MVS重建算法广泛应用于计算机视觉、计算机图形学和三维重建等领域。它们在各个领域都有应用，包括虚拟现实、3D建模、机器人和增强现实
不幸的是，由于缺乏基准数据集，很难定量地比较这些算法的性能，因此很难将研究重点放在最需要的发展领域。因此，作者希望通过本文对当前主流算法进行比较和评估，为该领域的进一步发展提供参考。
为了更准确地评估各种算法的重建结果，作者首先构建了一个包含高精度真实模型的数据集，并提出了一种新的评估方法。

数据集

左边的图片是作者使用的两个用于重建3D模型的物体。上面的是一个神庙的石膏复制品，下面的一个恐龙的石膏制品，这两个分别是它们的真实模型。右边的这张图表示的是这个神庙的数据（间隙是由于阴影造成的）

它分为三种情况

1. 整个半球面的总共317 个相机表示全部的视角
2. 蓝色和红色总共 47 个相机表示环形的视角
3. 红色的总共16 个相机表示稀疏环形的视角

评估方法

这篇论文的评估方法主要是为了比较多视角立体重建算法的效果。

为此作者提出了两个衡量指标

• 准确性：重建模型与真实的接近程度
• 完整性：与真实模型相比重建模型到底构建了多少

为了评估重建算法的效果作者假设重建的模型本身就是一个三角形网格
为了测量重建的准确性，作者计算重建的3D模型中的点和真实的3D模型上最近的点之间的距离
下图中 G 表示真实3D模型，R 表示要评估的算法的重建的结果

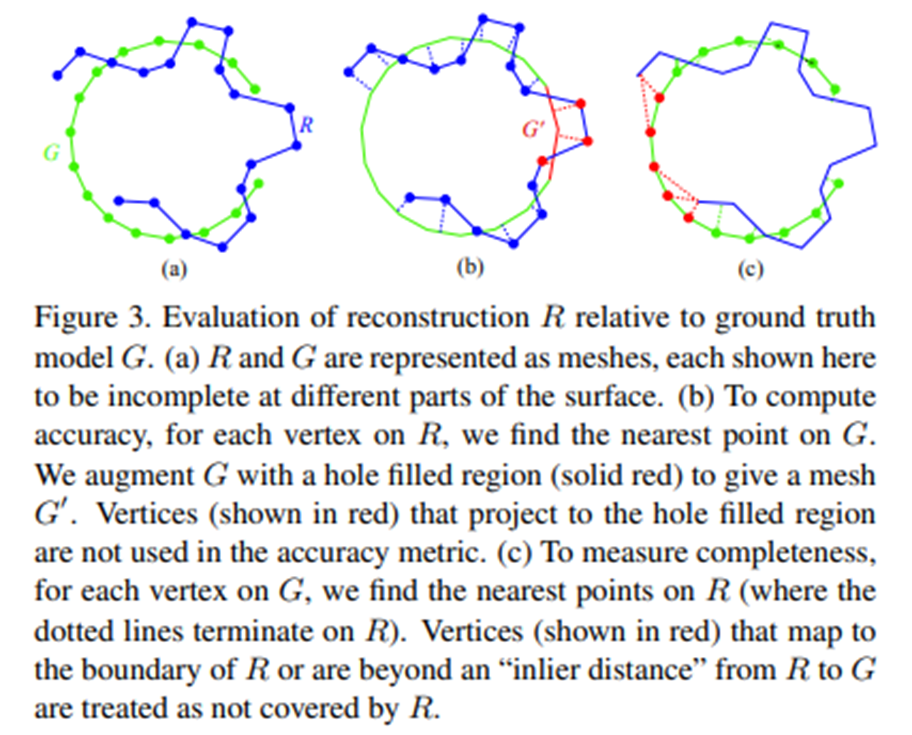
(由于 R 是⼀个曲⾯，理论上，作者应该需要对 R 进⾏积分，但在这篇文章中作者只是在 R 的顶点进行采样。)
但G 不完整时会出现问题。在这种情况下，对于 G 不完整区域中 R 上 的给定点，G 上最近的点可能位可能位于⽹格的较远部分。为了解决这个问题作者将原有的 G 进行填充，得到 G'，然后计算R上的点到 G' 上最近的点之间的距离。
作者使用由空间雕刻生成的孔洞填充表面，并进行多次扫描（每个物体大约 200 次），因此这些孔洞填充非常接近实际表面，然后选择一个准确性阈值 X ，这个 X 是一个百分比，以在阈值 X 内的点的最大距离作为重建模型的准确性。
为了测量完整性，作者计算从 G 到 R 的距离， 即与测量准确性相反的距离。直观地说，G 上没有合 适的 R 上最近点的点将被视为“未覆盖”。如图c中的，但这时候就不能用填充的方法来解决。
作者提出了一种替代的完整性度量方法，首先选择一个参数 d ，然后计算 G 上的点到 R 上最近的点之间的距离小于 d 的比例。比如图c G上总共有100个点，有90个点到R上最近的点之间的距离小于 d（像这些点），这边的红色有10个点的距离是大于 d 的，那重建的完整性就是90%。

结果

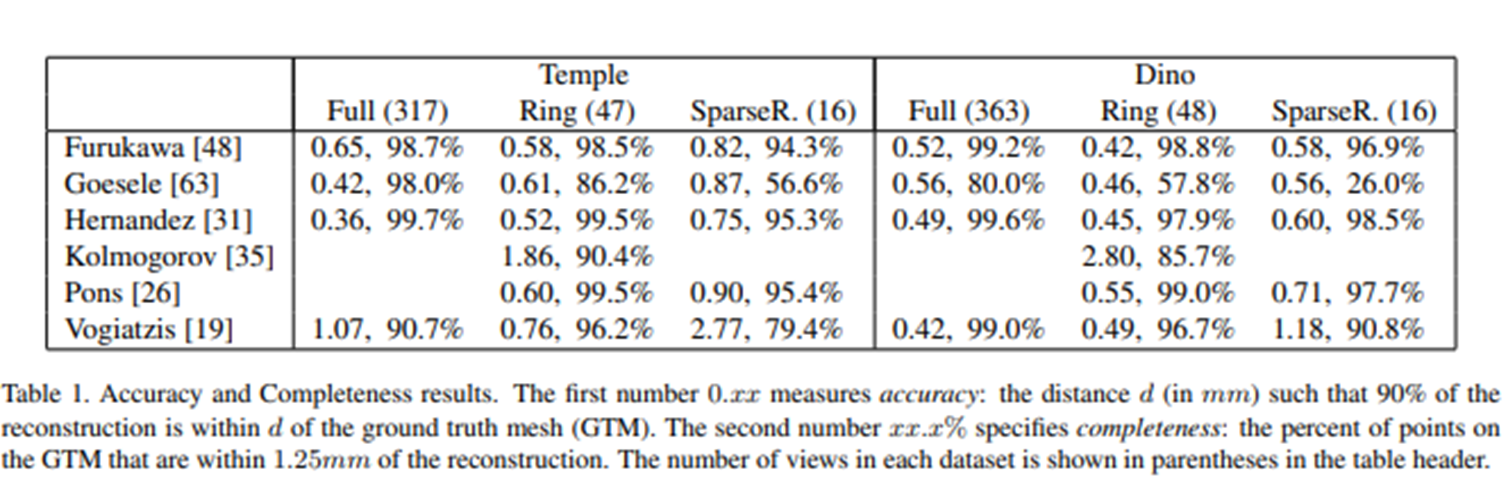
表 1 总结了对这六个人的算法的重建的模型上运行的准确性和完整性度量的结果。

• 为了计算准确性，作者使用 了 90% 的精度阈值，即 1.0mm 的精度意味着 90% 的点在 GTM 的 1mm 以内。
• 为了计算完整性，作者使 用了 1.25mm 的内部阈值，即 95% 的完整性意味着 95% 的点在 GTM 的 1.25mm 以内。