tensor张量数据结构

一、张量的基本属性

主要有三个属性：秩、轴、形状

• 秩：主要告诉我们是张量的维度，其实就是告诉我们是几维向量，通过多少个索引就可以访问到元素。
• 轴：在张量中，轴是指张量的一个维度。当处理多维数据时，每个维度都可以被称为一个轴。通常，第一个轴称为0轴（或轴0），第二个轴称为1轴（或轴1），以此类推。同索引从0开始计算
• 形状：形状是指张量在每个轴上的维度大小。它是一个由整数组成的元组，表示张量沿着每个轴的大小。
  

二、张量的直观理解

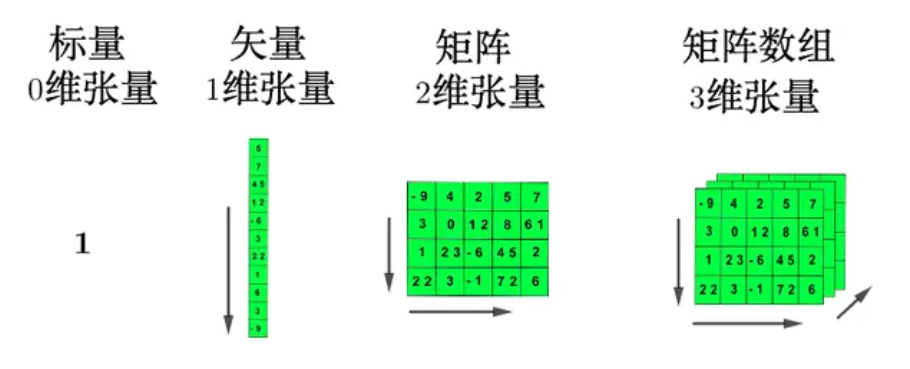
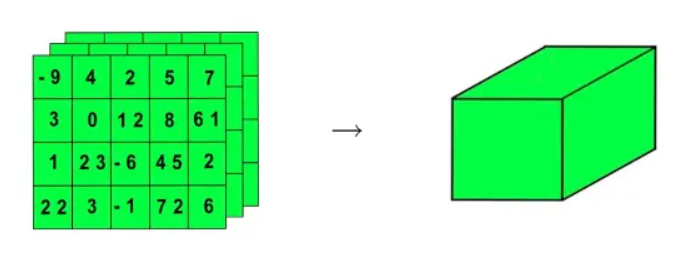
2.1把3维张量抽象成立方体

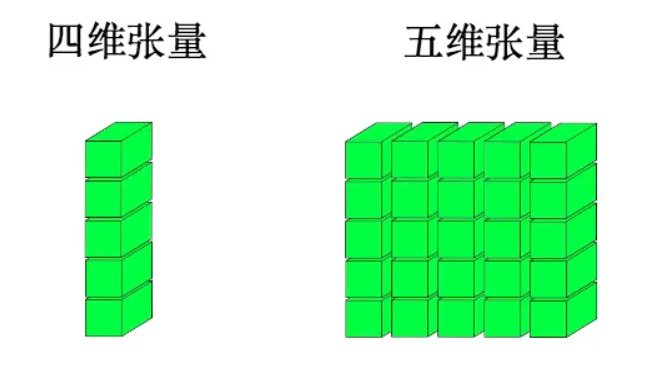
2.2更高维度

三、实践

3.1 0维张量（标量）

# 0维张量（标量）
tensor_0d = np.array(42)
print("0维张量：", tensor_0d)
print("维度：", tensor_0d.ndim)
print("形状：", tensor_0d.shape)

0维张量： 42
维度： 0
形状： ()

3.2 1维张量（向量）

#1维张量（向量）
tensor_1d = np.array([1, 2, 3])
print("1维张量：", tensor_1d)
print("维度：", tensor_1d.ndim)
print("形状：", tensor_1d.shape)

1维张量： [1 2 3]
维度： 1
形状： (3,)

3.3 2维张量（矩阵）

# 2维张量（矩阵）
tensor_2d = np.array([[1, 2], [3, 4]])
print("2维张量：\n", tensor_2d)
print("维度：", tensor_2d.ndim)
print("形状：", tensor_2d.shape)

2维张量：
 [[1 2]
 [3 4]]
维度： 2
形状： (2, 2)

3.4 3维张量

tensor_3d = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print("3维张量：\n", tensor_3d)
print("维度：", tensor_3d.ndim)
print("形状：", tensor_3d.shape)

3维张量：
 [[[1 2]
  [3 4]]

 [[5 6]
  [7 8]]]
维度： 3
形状： (2, 2, 2)

3.5 4维张量（例如：批量图像数据）

tensor_4d = np.random.rand(2, 3, 4, 4)  # 模拟批量为2，3通道，4x4像素的图像
print("4维张量（形状）：", tensor_4d.shape)
print("维度：", tensor_4d.ndim)

4维张量：
 [[[[0.76158905 0.50889347 0.71815367 0.69304463]
   [0.52520525 0.72555674 0.85270496 0.32378587]
   [0.59526167 0.32792191 0.50123455 0.10833325]
   [0.59880688 0.59677855 0.88285572 0.4809848 ]]

  [[0.36305307 0.06960381 0.92678542 0.59274188]
   [0.87533014 0.02521611 0.17350617 0.67618351]
   [0.18962636 0.09359039 0.04388708 0.87022525]
   [0.1629622  0.87446195 0.02532257 0.7190841 ]]

  [[0.0948755  0.19565576 0.01435343 0.71796839]
   [0.96410618 0.43856238 0.87676871 0.20652258]
   [0.33341796 0.19967975 0.43732216 0.44578688]
   [0.2204978  0.63834847 0.0398312  0.41826523]]]


 [[[0.76582446 0.28175843 0.75353101 0.01103086]
   [0.32532059 0.63380096 0.17306901 0.1625022 ]
   [0.05411325 0.73074117 0.66645972 0.46794851]
   [0.22031948 0.23594482 0.50791974 0.51469159]]

  [[0.60389647 0.86939317 0.36047495 0.37041494]
   [0.29389263 0.0907861  0.32717963 0.37871522]
   [0.46937278 0.62275192 0.45777425 0.97372567]
   [0.70629123 0.69301768 0.56032817 0.85254206]]

  [[0.03950869 0.90353414 0.05431898 0.47064513]
   [0.10020516 0.31592422 0.637032   0.03238864]
   [0.97464485 0.7579741  0.59497893 0.08251099]
   [0.19593545 0.50460934 0.29095014 0.1346555 ]]]]
4维张量（形状）： (2, 3, 4, 4)
维度： 4

四、加深理解

4.1什么是“维度”（Dimension / ndim）？

在张量中，维度（或称为“秩” rank）指的是你访问一个元素时需要提供的索引数量。

✅ 举个例子：

张量类型	示例	维度（ndim）	说明
0维（标量）	5	0	不需要索引，直接就是值
1维（向量）	[1, 2, 3]	1	要用一个索引，如 x[0]
2维（矩阵）	[[1, 2], [3, 4]]	2	需要两个索引，如 x[0][1]
3维张量	[[[1, 2], [3, 4]], [[5, 6], [7, 8]]]	3	需要三个索引，如 x[0][1][0]

📌 理解技巧：
维度 = 你访问一个具体数字需要下标几次。

4.2什么是“形状”（Shape / shape）？

形状是一个元组（tuple），表示张量在每个维度上的大小。

张量	形状（shape）	含义
5	()	0维，标量
[1, 2, 3]	(3,)	1维向量，长度为3
[[1, 2], [3, 4]]	(2, 2)	2维矩阵，2行2列
[[[1, 2], [3, 4]], [[5, 6], [7, 8]]]	(2, 2, 2)	3维张量：2块，每块2行2列
np.random.rand(3, 4, 5)	(3, 4, 5)	3维张量：3个4行5列的矩阵

4.3📌 总结对比：

概念	含义	示例
维度（ndim）	张量有多少个轴（axes）	0维：标量；1维：向量……
形状（shape）	每个轴上有多少个元素（元素数量分布）	(2, 3) 表示第一个轴有2个元素，第二个轴有3个

3维可以理解为“个数、行、列”

4.4更高维度理解

4.4.1✅ 4维张量例子

假设有一个4维张量，形状为 (N, C, H, W)，这在深度学习中经常用来表示一批图像数据：

• N：批次大小（Batch Size），表示有多少张图片。
• C：通道数（Channels），比如RGB图像有3个通道。
• H：高度（Height），图像的高度。
• W：宽度（Width），图像的宽度。

因此，你可以这样想：你有一堆相册（N），每个相册里有不同的照片集（C），每张照片都是由像素组成的二维网格（H x W）。

4.4.2🧩 5维张量例子

如果再增加一维，考虑一个形状为 (T, N, C, H, W) 的5维张量：
T：时间步长（Time Steps），如果你正在处理视频数据，那么T代表视频中的帧数。
其余四个维度保持不变，即批量大小（N）、通道数（C）、高度（H）和宽度（W）。

所以，5维张量可以被想象成一系列视频序列，其中每个序列包含多个帧（T），每个帧又由多张图片组成（N），每张图片有多条信息通道（C），每条通道上的图像是由像素组成的二维网格（H x W）。

五、张量的应用场景​

5.1你有一段 10 分钟的视频，想用深度学习来处理它（比如做动作识别、视频分类等），那怎么把它变成一个张量呢？

一、视频的基本结构

一段 10 分钟的视频，其实是由很多帧（frame）组成的，就像一本翻页动画一样。
📌 假设：
视频帧率是 30 FPS（每秒30帧）
视频时长是 10 分钟 = 600 秒
总帧数 = 30 × 600 = 18,000 帧
也就是说，这段视频可以看作是一个很长的帧序列：

[帧1, 帧2, 帧3, ..., 帧18000]

二、为什么要“分段”？怎么分？

1.为什么要分段？
因为：
18,000 帧的数据量太大，不能一次性输入模型。
模型一般处理的是固定长度的视频片段。
有些任务（如动作识别）只需要分析局部动作片段，而不是整个10分钟。
2.怎么分段？
常见的做法是：滑动窗口采样 或 均匀采样。

三、这些“片段”如何变成张量？

我们以一个片段为例来说明。
假设：
每个片段有 10 帧（T=10）
每帧是 RGB 图像（C=3），大小是 224×224（H=224, W=224）

(T, C, H, W) = (10, 3, 224, 224)

这里就是图片处理了，可以把10帧理解为10张图片

四、如果我要批量处理多个视频呢？

比如你有 32 个视频，每个视频取一个片段（10帧），那么输入张量的形状就是：

(N, T, C, H, W) = (32, 10, 3, 224, 224)

N=32：32 个视频
T=10：每个视频取10帧
C=3：RGB 三通道
H=224, W=224：图像尺寸
这就是一个 5维张量，它非常适合用于视频分类、动作识别等模型的输入。

五、个人疑问

训练时不用每一帧吗？32个视频每个只提取10帧吗？会不会太少。或者我可不可以理解为一段10分钟的视频分割为32段，每段包含10帧，这样是不是就全部提取到了

🎯 一、训练时是不是只用每个视频的10帧？会不会太少？

✅ 答案：
不是“只用”10帧，而是每次训练用10帧，但整个训练过程会遍历视频的所有帧。
这就像：
你有一个很长的句子，模型每次只看一部分（比如10个词），但通过多次训练，模型可以“看到”整个句子。
📌 举个例子：
你有一个视频有 1000 帧
每次训练取一个片段（10帧）
你可以使用 滑动窗口 或 随机采样 的方式：

• 第一次训练：帧 0~9
• 第二次训练：帧 5~14
• 第三次训练：帧 10~19
• ...
• 最后一次训练：帧 990~999

这样，整个训练过程中，模型就能看到整个视频的内容。

二、32个视频每个只提取10帧？

✅ 答案：
是的，在一次训练迭代（batch）中，每个视频只取10帧，但这不是“只取一次”，而是每次训练时都取不同的片段。

📌 举个例子：
你有 32 个视频（N=32）
每次训练时，从每个视频中随机采样10帧（T=10）
这些帧可能来自视频的不同部分（比如开头、中间、结尾）
这样做的目的是：

• 提高模型的泛化能力
• 防止模型只记住某一段内容

三、是不是可以把一个视频分成32段，每段10帧，这样就覆盖全部帧？

✅ 答案：
是的，这是一种更密集地覆盖视频内容的方法，常用于推理（inference）阶段，而不是训练。

📌 举个例子：
一个视频有 320 帧
你可以把它分成 32 段，每段 10 帧
每段输入模型，得到一个预测结果
最后把 32 个预测结果平均或融合，得到最终结果
这叫作 “多片段测试”（multi-crop testing）或“滑动窗口推理”

四、总结：训练 vs 推理中的不同处理方式

场景	目的	处理方式	张量形状
训练时	提高泛化能力，防止过拟合	每个视频随机采样 10 帧	(32, 10, 3, 224, 224)
推理时	充分利用视频信息，提高准确率	一个视频采样多个片段（如32段）	(32, 10, 3, 224, 224)

六、个人疑问

为什么采用批次训练，是希望最少的训练，获得接近真实的效果吗

为什么使用“批次训练”（Mini-batch Training）？
✅ 简短回答：
使用批次训练是为了在训练速度、内存占用和模型泛化能力之间取得最佳平衡。

📌 一、先说说“训练”的目标

我们的目标是让模型尽可能准确地学习数据的规律，也就是：

在训练数据上表现好 ✅
在新数据（测试数据）上也表现好（泛化能力强） ✅
为了达到这个目标，我们需要：

• 高效地计算梯度
• 稳定地更新参数
• 防止过拟合

二、三种训练方式对比

类型	每次训练使用的样本数	特点	优点	缺点
批量训练（Batch Training）	整个训练集	参数更新非常稳定	准确率高	计算慢，内存占用大，无法训练大数据集
随机训练（Stochastic Training）	1个样本	每次更新参数非常快	快速适应变化	更新不稳定，容易震荡，收敛困难
小批量训练（Mini-batch Training）	一小批（如32、64、128个）	折中方案	✅ 快速 + 稳定 + 内存可控	需要调参（如 batch size）

三、关于“希望最少的训练，获得接近真实的效果”这句话的理解

我们可以这样理解：

✅ “使用小批量训练，是为了在尽可能少的训练次数中，让模型学到数据的整体分布规律，从而在新数据上也有好的表现。”

也就是说：

• 不是“最少的训练”，而是“最有效的训练”。
• 用小批量数据，让每次更新都尽量接近真实梯度。
• 通过多次迭代，让模型逐步逼近全局最优解。