练习_第一个网络
代码及效果
import torch
import torch.nn.functional as F # 激励函数都在这
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# 画图
# plt.scatter(x.data.numpy(), y.data.numpy())
# plt.show()
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self, n_feature, n_hidden, n_output):
super().__init__() # 继承 __init__ 功能。# 更简洁,Python 3 推荐写法
# 定义每层用什么样的形式
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x): # 这同时也是 Module 中的 forward 功能
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1, n_hidden=10, n_output=1)
plt.ion() # 画图
plt.show()
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
for t in range(100):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
# 接着上面来
if t % 5 == 0:
# plot and show learning process
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.text(0.5, 0, 'Loss=%.4f' % loss.item(), fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
plt.ioff() # 停止画图
plt.show()
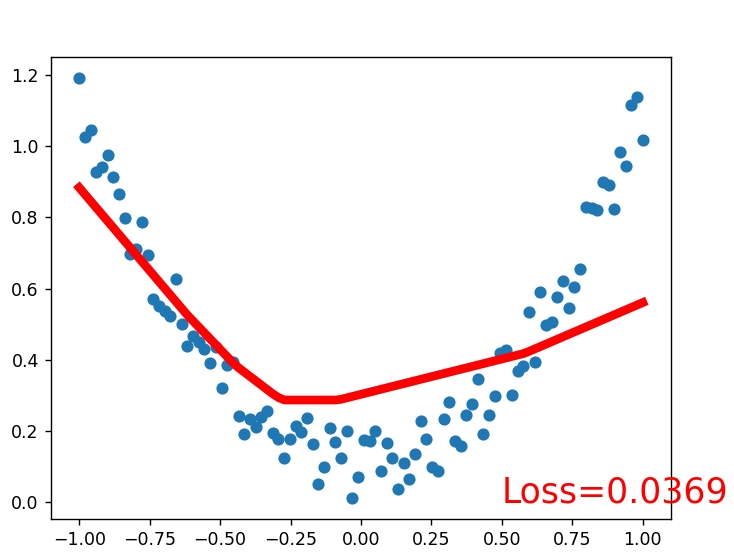
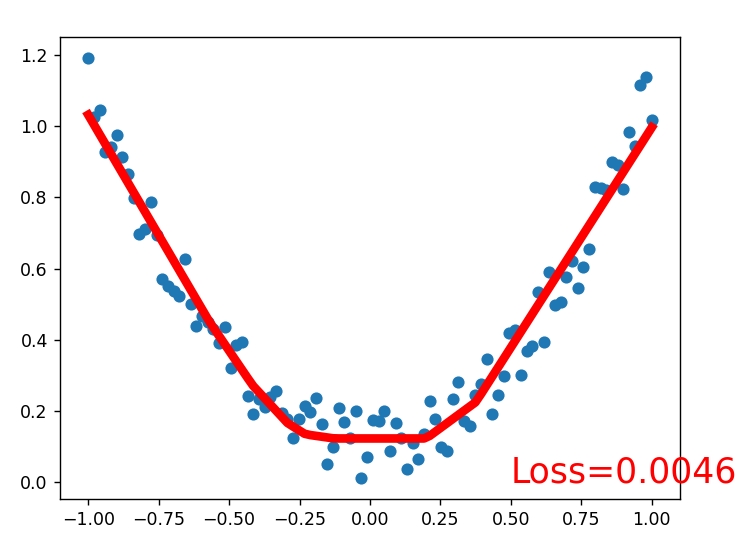
1建立数据集
我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它.
import torch
from torch.autograd import Variable
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()
1.1torch.linspace(-1, 1, 100)
[-1.0000, -0.9798, -0.9596, ..., 0.9596, 0.9798, 1.0000]
生成从-1到1之间的100个等间隔数值,形成一个一维张量,形状是 (100,)。
1.2torch.unsqueeze(..., dim=1)
[[-1.0000],
[-0.9798],
[-0.9596],
...
[ 0.9596],
[ 0.9798],
[ 1.0000]]
在第 1 维(列方向)增加一个维度,结果变成二维张量,形状为 (100, 1),这样更适合于神经网络输入。
1.3torch.rand(x.size()) 是什么
x 是一个 100 行、1 列的数据,x.size() 就是告诉别人:“我这个数据有 100 行、1 列”。
torch.rand(x.size()) 它是让 PyTorch 生成一个和 x 形状一样的随机数表,里面的数字是 0~1 之间的随机数。
2建立神经网络
这段代码定义了一个简单的两层神经网络,可以用来做回归任务(比如根据 x 预测 y),它的结构是:
输入层:1 个神经元
隐藏层:10 个神经元 + ReLU 激活函数
输出层:1 个神经元(没有激活函数)
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
# 定义每层用什么样的形式
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.predict = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x): # 这同时也是 Module 中的 forward 功能
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1, n_hidden=10, n_output=1)
2.1为什么必须写成__init__()
因为它是 Python 中的一个 魔法方法(Magic Method),它有特殊的含义和作用。
🔍 什么是魔法方法?
在 Python 中,以双下划线开头和结尾的方法(比如__init__、__str__等)是“魔法方法”,它们不是普通函数,而是被 Python 解释器特别对待的。
🔍__init__()是什么意思?
当你创建一个类的实例时,Python 会自动调用这个类的__init__() 方法。
2.2初始化
我这个类是从 torch.nn.Module 继承来的,请先运行它自带的初始化方法,然后再做我自己的初始化。
super(Net, self).__init__()#python 2
super().__init__()#python 3
❓ self 是什么?
self 是类的实例本身。
所有你想保存的数据、层、变量,都要通过 self.xxx = xxx 来保存。
后面你才能在其他方法中访问这些内容。
2.3torch.nn.Linear(n_hidden, n_output)
这是 PyTorch 中的一个全连接层(线性层)
in_features:输入特征的数量(输入维度)
out_features:输出特征的数量(输出维度)
2.4什么是 forward 函数
在 PyTorch 中:forward() 是每个神经网络类必须定义的方法,用于描述 输入数据是如何在网络中一层一层向前传递的。
你可以把它想象成:
“数据从入口进来,经过一系列变换,最后从出口出去”
这就是所谓的“前向传播”(Forward Propagation)。
2.4.1举个例子理解整个流程
输入 x = 2
↓
通过 hidden 层 → 得到线性输出(比如 [0.5, -0.3, 0.8, ..., 1.2])
↓
通过 ReLU → 负数变 0,变成 [0.5, 0, 0.8, ..., 1.2]
↓
通过 predict 层 → 得到最终输出(比如 1.7)
2.5forward()什么时候执行
forward() 是神经网络中的核心函数,它在你调用 net(x) 的时候自动执行,用于描述数据在网络中是如何一层一层向前传递的。
🔍 为什么可以这样写?net(x) 是怎么变成调用 forward() 的?
这是因为 PyTorch 的 torch.nn.Module 类已经帮你做了这件事:
所有继承自 torch.nn.Module 的类,都可以像函数一样被调用(比如 net(x))
它们的 forward() 方法会被自动调用
2.5.1前向传播流程图(简单版)
输入 x
↓
net(x) ←←← 触发 forward()
↓
forward(x) 函数开始执行:
↓
经过 hidden 层 → ReLU 激活 → predict 输出层
↓
返回输出结果 y
3训练网络
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.5) # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
for t in range(100):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
3.1训练流程图
输入数据 x ─→ net(x) ─→ 得到预测值 prediction
↓
loss = MSE(prediction, y)
↓
loss.backward() → 计算梯度
↓
optimizer.step() → 更新参数
整个训练循环就是一个“喂数据 → 算误差 → 反向传播 → 更新参数”的过程,重复多次后,模型就能学会数据中的规律。
3.2x是100行1维,y也是100行1维吗?loss_func是计算每行对应的y吗?
执行过程详解
- prediction = net(x)
把所有 100 个样本一次性喂给神经网络
网络会为每个样本输出一个预测值
所以 prediction 的形状也会是 (100, 1)
你可以把它理解成
输入 x ┌─────┐ 输出 prediction
┌──────┐ │ │ ┌──────────┐
│x[0] │ ─→ │ net │ ─→ │pred[0] │
├──────┤ │ │ ├──────────┤
│x[1] │ ─→ │ │ ─→ │pred[1] │
├──────┤ │ │ ├──────────┤
│ ... │ │ │ │ ... │
├──────┤ │ │ ├──────────┤
│x[99] │ ─→ │ │ ─→ │pred[99] │
└──────┘ └─────┘ └──────────┘
- loss = loss_func(prediction, y)
这里使用的是 MSELoss(),即均方误差损失函数
它会对每一个样本的预测值和真实值做差平方,然后取平均
所以:
✅ loss_func 确实是对每一行的预测值和真实值分别计算误差,最后求平均。
3.3清空梯度(Zero Grad)
optimizer.zero_grad() # 清空上一次的梯度,防止累加
每次反向传播后,PyTorch 会把梯度保存下来
如果不清空,下次计算的梯度就会叠加上去,导致错误
3.4反向传播(Backward Pass)
loss.backward() # 反向传播,计算每个参数的梯度
根据当前的损失值,计算出每个参数对损失的影响(也就是梯度)
PyTorch 会自动帮你完成链式法则(Chain Rule)的求导过程
梯度会被保存在 .grad 属性里
3.5参数更新(Step)
optimizer.step() # 使用优化器将梯度应用到参数上,完成一次更新
这一步才是真正地“训练”模型
根据计算出的梯度和学习率,更新网络中的权重和偏置
模型通过不断学习,逐渐变得更准确


 浙公网安备 33010602011771号
浙公网安备 33010602011771号