分块进阶
分块进阶
分块的其他用法
P3793 由乃救爷爷
题意
题意是说对于一个长度为 \(n\) 的 \(a\) 序列有 \(m\) 次询问,每一次需要回答一个区间的最大值大小
时限 : 5s
内存 : 500MB
思路
\(st\)表
由于没有修改,全都是查询,可以想到 \(st\) 表
\(st\) 表需要 \(O(n\;log\,n)\) 的时间预处理,在此查询只需要 \(O(1)\) 单从时间上来看是可以通过这道题的,但是空间也许要 \(O(n\;log\,n)\) 的时间复杂度,显然超过了限制
分块
分块中的空间复杂度是在限制之内的
可是分块的每一次查询都有 \(O(3\sqrt{n})\) 的时间复杂度 \(2e7\) 的查询次数显然超时
分块 \(+\) \(st\)表
既然 分块 和 \(st\)表 都不能通过这题,那么可以考虑把两个结合起来
回忆一下分块求最大值的过程
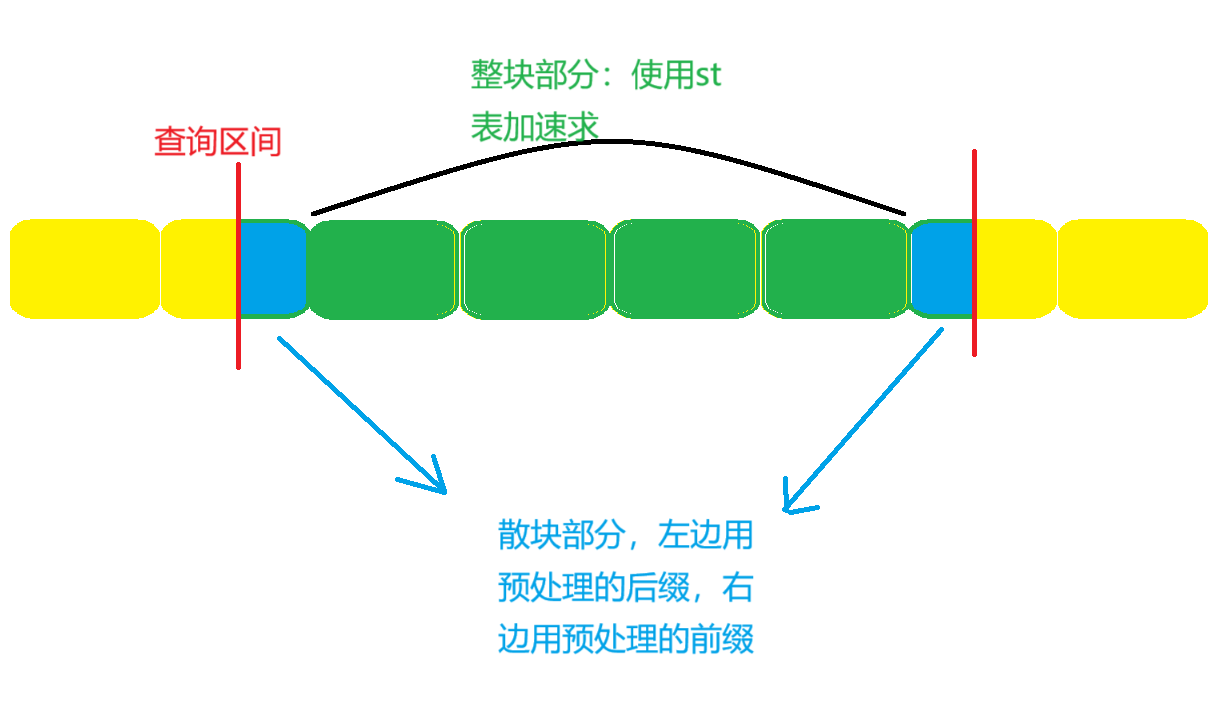
1.整块
第一个部分是中间的完整块,如果对每一完整快一个一个取最大值,显然超时,所以需要瞬间求出这一部分的最大值
可以想到用 \(st\) 表加速这个过程!
将每一个块当做一个元素,放在 \(st\)表 里预处理,\(st[\,i\,][\,j\,]\) 就表示从第 \(i\) 个「块」开始的 \(2^j\) 个块内的最大值
这样预处理完成之后就可以 \(O(1)\) 的时间得到一堆完整块的最大值
空间发复杂度上因为最多是有 \(\sqrt{n}\) 个「块」,所以可以接受
2.散块
一个区间的答案一定是有至多两个散块和若干个整块拼接出来的
原来暴力求散块的最大值方法不行,依然思考预处理。
可以发现答案一定是第一个散块的后缀最大值,和第二个散块的前缀最大值,可以提前预处理,这样就可以直接得到散块内的最大值
整体的复杂度已经可以接受,但是如果查询区间处于同一个块内,那就只能暴力求,依然有 \(O(\sqrt{n})\) 的复杂度,但是题目数据没有这么强,可以通过
但是这个代码的这个地方还能再优化
配图
code
#include<bits/stdc++.h>
#define int unsigned
#define fore(i,a,b) for( int i=(a); i<=(b); ++i)
#define repe(i,a,b) for( int i=(a); i>=(b); --i)
using namespace std;
namespace GenHelper
{
unsigned z1,z2,z3,z4,b;
unsigned rand_()
{
b=((z1<<6)^z1)>>13;
z1=((z1&4294967294U)<<18)^b;
b=((z2<<2)^z2)>>27;
z2=((z2&4294967288U)<<2)^b;
b=((z3<<13)^z3)>>21;
z3=((z3&4294967280U)<<7)^b;
b=((z4<<3)^z4)>>12;
z4=((z4&4294967168U)<<13)^b;
return (z1^z2^z3^z4);
}
}
void srand(unsigned x)
{using namespace GenHelper;
z1=x; z2=(~x)^0x233333333U; z3=x^0x1234598766U; z4=(~x)+51;}
int read()
{
using namespace GenHelper;
int a=rand_()&32767;
int b=rand_()&32767;
return a*32768+b;
}
const int N=2e7+10;
const int qN=4e3+500;
int n,T,s;
int L[qN],R[qN],a[N];
int q[N],p[N];
int pos[N],st[qN][20];
int logg[qN];
void init(){
int len=sqrt(n);
int num=(n+len-1)/len;
for(int i=1;i<=num;i++){
L[i]=(i-1)*len+1;
R[i]=i*len;
}
if(R[num]>n)R[num]=n;
for(int i=1;i<=num;i++){
for(int j=L[i];j<=R[i];j++){
pos[j]=i;
st[i][0]=max(st[i][0],a[j]);
}
p[L[i]]=a[L[i]];
q[R[i]]=a[R[i]];
for(int j=L[i]+1;j<=R[i];j++){
p[j]=max(p[j-1],a[j]);
}
for(int j=R[i]-1;j>=L[i];j--){
q[j]=max(q[j+1],a[j]);
}
}
logg[1]=0;
for(int i=2;i<=num;i++)logg[i]=logg[i>>1]+1;
for(int j=1;(1<<j)<=num;j++){
for(int i=1;i+(1<<j)-1<=num;i++){
st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]);
}
}
return;
}
int query_st(int l,int r){
if(l>r)return 0;
int k=logg[r-l+1];
return max(st[l][k],st[r-(1<<k)+1][k]);
}
unsigned long long ans_sum=0;
int query(int l,int r){
if(l>r)swap(l,r);
int x=pos[l],y=pos[r];
int tmp=0;
if(x==y){
for(int i=l;i<=r;i++)tmp=max(tmp,a[i]);
}
else{
tmp=query_st(x+1,y-1);
tmp=max(tmp,max(q[l],p[r]));
}
return tmp;
}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>T>>s;
srand(s);
for(int i=1;i<=n;i++){
a[i]=read();
}
init();
while(T--){
int l=read()%n+1,r=read()%n+1;
if(l>r)swap(l,r);
ans_sum+=query(l,r);
}
cout<<ans_sum<<'\n';
return 0;
}
P4879 ycz的妹子
唯一难点在于删除操作,要找到第x个没有被删掉的点
可以对每一个分块记录还在的点,对每个点记录是否还在
最后要找到第x个点,就从头遍历每一个分块,如果点数不足x,就减去,说明还在后面的分块,如过达到,就在分块内部找当前已经减剩下的第x个点
标记,更新分块信息
注意加入操作会加入新的点,提前把\(1e6\)个点预处理到每一个分块里,新加入的直接操作,注意标记成已存在,不能用0表示是否存在,点权有可能为0
code
#include<bits/stdc++.h>
#define int long long
#define fore(i,a,b) for( int i=(a); i<=(b); ++i)
#define repe(i,a,b) for( int i=(a); i>=(b); --i)
using namespace std;
const int N=1e6+10;
int n,m;
int a[N],vis[N],siz[N],L[N],R[N],pos[N],sum[N];
void init(){
int maxn=1e6;
int len=sqrt(maxn);
int num=(maxn+len-1)/len;
for(int i=1;i<=num;i++){
L[i]=(i-1)*len+1;
R[i]=i*len;
}
R[num]=maxn;
for(int i=1;i<=num;i++){
for(int j=L[i];j<=R[i];j++){
pos[j]=i;
sum[i]+=a[j];
siz[i]+=vis[j];
}
}
return;
}
void change_c(int x,int y){
if(vis[x]==0)return;
sum[pos[x]]-=a[x];
a[x]-=y;
sum[pos[x]]+=a[x];
return;
}
void change_i(int x,int y){
if(vis[x]){
sum[pos[x]]-=a[x];
a[x]=y;
sum[pos[x]]+=a[x];
}
else{
vis[x]=1;
sum[pos[x]]-=a[x];
a[x]=y;
sum[pos[x]]+=a[x];
siz[pos[x]]+=1;
}
return;
}
void change_d(int x){
int num=1;
while(x-siz[num]>0){
x-=siz[num];
num++;
}
for(int i=L[num];i<=R[num];i++){
if(x-vis[i]==0){
if(x-vis[i]==0){
siz[num]--;
sum[num]-=a[i];
vis[i]=a[i]=0;
return;
}
}
else{
x-=vis[i];
}
}
return;
}
int query(){
int res=0;
for(int i=1;i<=pos[1000000];i++){
res+=sum[i];
}
return res;
}
signed main(){
ios::sync_with_stdio(false);
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
vis[i]=1;
}
init();
for(int i=1;i<=m;i++){
char orr;
int x,y;
cin>>orr;
if(orr=='C'){
cin>>x>>y;
change_c(x,y);
}
if(orr=='I'){
cin>>x>>y;
change_i(x,y);
}
if(orr=='D'){
cin>>x;
change_d(x);
}
if(orr=='Q'){
cout<<query()<<'\n';
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号