第一周Day1 7.10
第一讲 枚举
例题
1.ABC猜想
枚举\(A\)和\(B\),那\(C\)的范围就是\(B\)~\(N/A/B\),当\(B \leq N/A/B\)时,\(C\)的个数就是\(N/A/B-B\)。
其中\(A\)的枚举范围是\(A*A*A \leq N\),\(B\)的枚举范围是\(A*B*B \leq N\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
int ans;
signed main(){
cin >> n;
for(int i = 1;i*i*i <= n;++ i){
for(int j = i;i*j*j <= n;++ j){
int k = n/i/j;
if(k >= j)
ans += k-j+1;
else break;
}
}
cout << ans;
return 0;
}
2.等差树
首先可以发现,答案的位数一定和\(X\)的位数相同。因为\(k\)位的最大等差数是\(k\)个\(9\),那么不管是\(X\)是什么,相同位数个\(9\)一定大于等于它。
那么枚举首项(\(1\)$9$)和公差($-9$\(9\)),判断这个等差数是否大于\(X\)即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
char x[25];
int a[25];
signed main(){
cin >> x;
int n = strlen(x);
for(int i = 1;i <= n;++ i)
a[i] = x[i-1]-'0';
for(int d = 1;d <= 9;++ d){
for(int t = -9;t <= 9;++ t){
int b = d;
bool fl = 1;
bool hav = 0;
for(int i = 1;i <= n;++ i){
if(b > 9||b < 0){
fl = 0;
break;
}
if(!hav){
if(b > a[i]) hav = 1;
if(b < a[i]){
fl = 0;
break;
}
}
b += t;
}
if(fl){
b = d;
for(int i = 1;i <= n;++ i)
cout << b,b += t;
return 0;
}
}
}
return 0;
}
3.M <= ab
我们假设一下\(a \leq b\)。
首先特殊情况:
1.如果\(n^2 \leq m\),那么一定不行。
2.如果\(n \geq m\),那么答案是\(m\)。
如果不是特殊情况,枚举\(a\),那么\(b = \lceil M/a \rceil\),判断一下\(b\)是否小于\(N\)即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
signed main(){
cin >> n >> m;
if(n < m/n||(m%n != 0&&n == m/n)){
cout << -1;
return 0;
}
if(n >= m){
cout << m;
return 0;
}
int t = sqrt(m)+3;
int ans = 1e18;
for(int a = 1;a <= t&&a <= n;++ a){
int b = (m+a-1)/a;
if(b > n) continue;
ans = min(ans,a*b);
}
cout << ans;
return 0;
}
4.开罐
罐装
把物品分成三类存。
贪心一下。三类都按\(X_i\)从大到小排序。
枚举选择几个普通罐头,这样就可以知道要用几个开罐器,剩下的就是易拉罐头的数量。(这三个都从大到小取)
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int m,n;
vector<int> v[3];
int ans;
int qzh[200005];
bool cmp(int a,int b){
return a > b;
}
signed main(){
cin >> n >> m;
for(int i = 1;i <= n;++ i){
int t,x;
cin >> t >> x;
v[t].push_back(x);
}
sort(v[0].begin(),v[0].end(),cmp);
sort(v[1].begin(),v[1].end(),cmp);
sort(v[2].begin(),v[2].end(),cmp);
for(int i = 1;i <= v[0].size();++ i) qzh[i] = qzh[i-1]+v[0][i-1];
int j = 0,gs = 0;
int da = 0;
ans = qzh[min((int)v[0].size(),m)];
for(int i = 0;i < v[1].size();++ i){
int x = v[1][i];
if(gs < i+1){
if(j+1 <= v[2].size()){
j++;
gs += v[2][j-1];
}
else break;
}
da += x;
if(i+1+j > m) break;
ans = max(ans,da+qzh[min((int)v[0].size(),m-i-1-j)]);
}
cout << ans;
return 0;
}
5.护城河
转换一下,把护城河转化为选哪些格子。
枚举选哪些格子,那么要符合什么条件呢?
1.联通,就是所有选的格子都可以互相走到,那么从一个开始\(bfs\),要能走到所有选的格子。
2.中间没有空格子,就是没有“回”字形。其实就是所有外围的格子互相联通,那么我们建一个超级源点,连所有边上的格子,从这个超级源点要能走到所有没有选的格子。
点击查看代码
#include<bits/stdc++.h>
#define fir first
#define sec second
using namespace std;
const int maxs = (1<<16)-1;
int a[20];
map<pair<int,int>,int> m1;
map<int,pair<int,int> > m2;
vector<int> v;
vector<int> e[20];
bool vs[20];
vector<int> bein;
bool pd(int s){
bool fl = 1;
for(int i = 0;i < v.size();++ i){
if(((s>>v[i])&1) == 0) return 0;
}
bein.clear();
for(int i = 0;i < 16;++ i){
int t = (s>>i)&1;
a[i] = t;
if(t == 1) bein.push_back(i);
}
queue<int> q;
memset(vs,0,sizeof(vs));
q.push(bein[0]);
vs[bein[0]] = 1;
while(!q.empty()){
int x = q.front();q.pop();
for(auto y:e[x]){
if(a[y] == 1&&!vs[y]){
q.push(y);
vs[y] = 1;
}
}
}
for(auto x:bein)
if(!vs[x]) return 0;
memset(vs,0,sizeof(vs));
q.push(16);
vs[16] = 1;
while(!q.empty()){
int x = q.front();q.pop();
for(auto y:e[x]){
if(a[y] == 0&&!vs[y]){
q.push(y);
vs[y] = 1;
}
}
}
for(int i = 0;i < 16;++ i){
if(a[i] == 0&&!vs[i]) return 0;
}
return 1;
}
int dx[] = {0,1,-1,0,0};
int dy[] = {0,0,0,1,-1};
signed main(){
for(int i = 1;i <= 4;++ i)
for(int j = 1;j <= 4;++ j){
int w;
cin >> w;
int t = (i-1)*4+j-1;
m1[{i,j}] = t;
m2[t] = {i,j};
if(w == 1) v.push_back(t);
}
for(int x = 1;x <= 4;++ x){
for(int y = 1;y <= 4;++ y){
for(int k = 1;k <= 4;++ k){
int xx = x+dx[k];
int yy = y+dy[k];
if(xx > 4||xx < 1||yy > 4||yy < 1)
continue;
e[m1[{x,y}]].push_back(m1[{xx,yy}]);
}
if(x == 1||x == 4||y == 1||y == 4){
//e[m1[{x,y}]].push_back(16);
e[16].push_back(m1[{x,y}]);
}
}
}
int ans = 0;
for(int s = 0;s <= maxs;++ s){
if(!pd(s)) continue;
ans++;
}
cout << ans;
return 0;
}
6.CSP2022-S-1- 假期计划
这个题比较复杂。
首先,这个图是无向图,所以它是具有对称性的,也就是说,\(c \to d \to 1\)和\(1 \to d \to c\)是一样的,那么\(1 \to a \to b\)和\(1 \to d \to c\)是完全一样的两部分,所以我们拆成两部分计算。
这是前提。
我们来考虑一下经过点数小于等于\(k\)的限制,也就是说经过边数小于等于\(k+1\)。
考虑一下建一个新图。我们以每一个点为起点做\(n\)次最短路,然后每次从\(n\)个点中找出任意两个点,如果这两个点的距离小于等于\(k+1\),那么在新图上连一条这两个点之间的边,所以我们就把经过边数小于等于\(k+1\)的限制转化为了在新图上只能走一步。
接着来,\(1 \to a \to b\)这样的问题怎么做?
我们记一个\(g_b = a\)代表从\(1\)走到\(a\)再走到\(b\)分数最大,那么分数就是\(s_a + s_b\)。
这个怎么求?枚举\(1\)的每一个出边\(x\),再枚举\(x\)的每一个出边\(y\),用\(x\)更新\(g_y\)。
我们枚举\(b\)和\(c\),这样我们就可以找到让分数最大的\(a\)和\(d\),那么问题又来了,如果\(a = d\)或者\(a = c\)或者\(b = d\)怎么办?
那么我们多记几个,记分数最大的,次大的,次次大的,记三个,因为换三次一定不会再相同了,就拿\(a\)来说吧,可能第一次等于\(d\),换了一次又等于\(c\),那么再换一次就不会重复了。
那么两边都可以换,换那一边的第几大呢?可以枚举每一种情况,因为总共每一边就三种情况,组合起来才九种情况,枚举一下即可。
tips:其实记分数最大的,次大的,次次大的并不是很好记,那么我们就把每一种过来的情况都记录下来,然后按分数降序排个序然后每次取前三个即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,k;
int sc[2505];
vector<int> ed[2505];
vector<int> e[2505];
int ds[2505][2505];
void dijk(int s){
memset(ds[s],0x3f,sizeof(ds[s]));
ds[s][s] = 0;
queue<int> q;
q.push(s);
while(!q.empty()){
int x = q.front();q.pop();
for(auto y:ed[x]){
if(ds[s][y] > ds[s][x]+1){
ds[s][y] = ds[s][x]+1;
q.push(y);
}
}
}
}
vector<int> g[2505];
bool cmp(int a,int b){
return sc[a] > sc[b];
}
signed main(){
freopen("holiday.in","r",stdin);
freopen("holiday.out","w",stdout);
cin >> n >> m >> k;
for(int i = 2;i <= n;++ i) cin >> sc[i];
for(int i = 1;i <= m;++ i){
int x,y;
cin >> x >> y;
ed[x].push_back(y);
ed[y].push_back(x);
}
for(int i = 1;i <= n;++ i)
dijk(i);
for(int x = 1;x <= n;++ x){
for(int y = 1;y <= n;++ y){
if(x == y) continue;
if(ds[x][y] <= k+1)
e[x].push_back(y);
}
}
for(auto x:e[1]){
for(auto y:e[x])
if(y != 1) g[y].push_back(x);
}
for(int i = 2;i <= n;++ i)
sort(g[i].begin(),g[i].end(),cmp);
int ans = 0;
for(int b = 2;b <= n;++ b){
for(int c = b+1;c <= n;++ c){
if(ds[b][c] <= k+1){
for(int i = 0;i < min(3ll,(int)g[b].size());++ i){
for(int j = 0;j < min(3ll,(int)g[c].size());++ j){
if(g[b][i] == g[c][j]||g[b][i] == c||b == g[c][j]) continue;
ans = max(ans,sc[g[b][i]]+sc[b]+sc[c]+sc[g[c][j]]);
}
}
}
}
}
cout << ans;
return 0;
}
7.找四元环
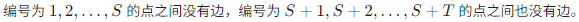
注意到这句话,这是一个二分图。
我们考虑一个四元环长什么样?
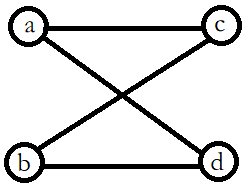
(画成了二分图的样子)
我们发现二分图的有一半(\(T\)那一半,这里我们认为\(c\)和\(d\)是在\(T\)那一半的)只有\(3000\),那么我们可以枚举\(c\)和\(d\),那么我们就要找到\(a\)和\(b\)两个另一半的点,使得\(c\)和\(d\)都向它们两个有连边。
怎么做呢?
我们可以枚举\(a\)和\(b\)那一半的每个点的所有出边,例如\(x\)的出边是\(y_1\),\(y_2\),\(y_3\),……,\(y_k\),我们把它们两两组对,就是\(y_1\)和\(y_2\),\(y_1\)和\(y_3\),\(y_1\)和\(y_4\),……,\(y_{k-1}\)和\(y_k\),那么这些对\(c\)和\(d\)那一半的点都同时连向\(x\)。
那么我们可以开一个\(vector\),记录每一对\(c\)和\(d\)那一半的点同时连向哪些点,这时我们把这些对的\(vector\)增加一个\(x\)即可。
做完了这个,我们接着说枚举\(c\)和\(d\),那么我们只需要看看这对点同时连向哪些点,只要多于两个即可输出。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int s,t,m;
vector<int> v[3005][3005];
vector<int> e[300005];
vector<int> px;
signed main(){
cin >> s >> t >> m;
for(int i = 1;i <= m;++ i){
int u,v;
cin >> u >> v;
e[u].push_back(v);
}
for(int i = 1;i <= s;++ i){
sort(e[i].begin(),e[i].end());
for(int j = 0;j < e[i].size();++ j){
for(int k = j+1;k < e[i].size();++ k){
int a = e[i][j]-s;
int b = e[i][k]-s;
v[a][b].push_back(i);
if(v[a][b].size() >= 2){
px.push_back(v[a][b][0]);
px.push_back(i);
px.push_back(a+s);
px.push_back(b+s);
sort(px.begin(),px.end());
for(auto x:px) cout << x << " ";
return 0;
}
}
}
}
cout << -1 << endl;
return 0;
}
作业
1.简单背包问题
比较好想。
由于\(w_1 \leq w_i \leq w_1+3\),重量只有四种,我们按重量分四类存储,每一类从大到小排列,枚举每一类选多少个判断一下重量合不合适即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m;
vector<int> wei[5];
vector<int> sum[5];
bool cmp(int a,int b){
return a>b;
}
signed main(){
cin >> n >> m;int w1;
for(int i = 0;i < 4;++ i) wei[i].push_back(0);
for(int i = 1;i <= n;++ i){
int w,v;
cin >> w >> v;
if(i == 1) w1 = w;
wei[w-w1].push_back(v);
}
for(int i = 0;i < 4;++ i){
sort(wei[i].begin()+1,wei[i].end(),cmp);
sum[i].resize(wei[i].size());
for(int j = 1;j < wei[i].size();++ j)
sum[i][j] = sum[i][j-1]+wei[i][j];
}
int ans = 0;
for(int i = 0;i < wei[0].size();++ i){
for(int j = 0;j < wei[1].size();++ j){
for(int k = 0;k < wei[2].size();++ k){
for(int l = 0;l < wei[3].size();++ l){
int wght = (i+j+k+l)*w1+j+k+k+l+l+l;
if(wght > m) break;
ans = max(ans,sum[0][i]+sum[1][j]+sum[2][k]+sum[3][l]);
}
}
}
}
cout << ans;
return 0;
}
2.好数
枚举\(x\)和\(y\),判断是否被\(K\)整除和除完了是否为平方数即可。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,k;
map<int,int> mp;
int ans;
signed main(){
cin >> k >> n;
for(int x = 1;x*x*x*x*x*x <= n;++ x){
for(int y = 1;y*y*y*y <= n;++ y){
int w = x*x*x*x*x*x+y*y*y*y;
if(w > n) break;
if(w%k == 0){
int zz = w/k;
int z = sqrt(zz);
if(z*z == zz){
if(!mp[w]) ans++;
mp[w] = 1;
}
}
}
}
cout << ans;
return 0;
}
3.立方差
4.和积之比
化简一下这个式子。
\(\frac{x_i+x_j+x_k}{x_ix_jx_k} = \frac{x_i}{x_ix_jx_k}+\frac{x_j}{x_ix_jx_k}+\frac{x_k}{x_ix_jx_k} = \frac{1}{x_jx_k}+\frac{1}{x_ix_k}+\frac{1}{x_ix_j}\)
我们记\(d_i = \frac{1}{x_i}\),那么上面的式子可以进一步化为\(d_jd_k+d_id_k+d_id_j\)。
我们以最大值为例。
\(d_jd_k+d_id_k+d_id_j = d_i(d_j+d_k)+d_jd_k\),那么我们如果确定了\(j\)和\(k\),\(i\)肯定越大越好。
\(j\)和\(k\)也同理,如果确定了另两个,一定是越大越好。
那么三个数就都是越大越好。
那么我们直接取出最大的三个和最小的三个,组合一下去最大值和最小值即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n;
double x[200005];
vector<double> v;
double xiao = 100000000;
double da = -100000000;
signed main(){
cin >> n;
for(int i = 1;i <= n;++ i){
int d;
cin >> d;
x[i] = 1.0/(d*1.0);
}
sort(x+1,x+1+n);
if(n >= 6){
v.push_back(x[1]);
v.push_back(x[2]);
v.push_back(x[3]);
v.push_back(x[n]);
v.push_back(x[n+1]);
v.push_back(x[n+2]);
}
else{
for(int i = 1;i <= n;++ i)
v.push_back(x[i]);
}
int m = v.size();
for(int i = 0;i < m;++ i){
for(int j = 0;j < m;++ j){
for(int k = 0;k < m;++ k){
if(i != j&&j != k&&i != k){
double t = v[i]*v[j];
t += v[j]*v[k]+v[k]*v[i];
xiao = min(xiao,t);
da = max(da,t);
}
}
}
}
printf("%.15lf\n%.15lf",xiao,da);
return 0;
}
5.数字和
首先考虑两个性质
1.当\(\sqrt{n} < b < n\)时,\(n\)的\(b\)进制只有两位。
2.当\(b \geq n\)是,\(n\)的\(b\)进制各个数位之和就是\(n\)。
所以我们可以特判一下性质2:如果\(n = s\),输出\(n\)。
这时剩下的就还有两部分,\(b \leq \sqrt{n}\)和\(b > \sqrt{n}\)。
对于前一部分,枚举每一个\(b\)暴力判断是否等于\(s\)。
后一部分有点麻烦。
我们先假设这个\(b\)合法。
我们把\(n\)转化为\(b\)进制,那么第一位是\(\lfloor \frac{n}{b} \rfloor\),第二位是\(n\)%\(b\)。
想一下除法算式,那么\(\lfloor \frac{n}{b} \rfloor\)就是商,\(n\)%\(b\)就是余数。
记\(p = \lfloor \frac{n}{b} \rfloor\),\(q = n\)%\(b\),那么有\(p+q = s\),\(b = \frac{n-q}{p}\)。
那么枚举\(p\),根据\(p+q = s\)算出\(q\),根据\(b = \frac{n-q}{p}\)算出\(b\)。
我们考虑现在有了这些东西,那么要怎么样\(b\)才合法呢?
1.\(b \geq 2\)
2.\(0 \leq q < b\),余数的要求
3.\(p < b\),如果\(p \geq b\)就又要进位了。
4.\(b*p+q = n\),也就是判断那个分数能不能整除。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,s;
int ans = 1e18;
signed main(){
cin >> n >> s;
if(n == s){
cout << n+1;
return 0;
}
for(int b = 2;b*b <= n;++ b){
int sum = 0;
int t = n;
while(t){
sum += t%b;
t /= b;
}
if(sum == s){
ans = min(ans,b);
}
}
for(int p = 1;p*p <= n;++ p){
int q = s-p;
int b = (n-q)/p;
if(b >= 2&&b*p+q == n&&q < b&&q >= 0&&p < b){
ans = min(ans,b);
}
}
if(ans == 1e18) cout << -1;
else cout << ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号