2024国庆S综合强化Day3

今天的题比较简单。

A 友矩阵

link

人话翻译一下题目中的条件。

1.和相等。
2.左上角相同。
3.右下角不同。
4.长宽之和相同（周长相同）。
5.长宽之差互为相反数（一个长减宽，一个宽减长）。

我们可以证明一下两个矩形如果互为满足2.3.4.5.条的友矩阵，一定是左上角重合一个横着一个竖着的两个相同长方形（如图黄色和绿色的长方形）。

证明：设两个长方形互为友矩阵，一个的长宽分别为\(x\)、\(y\)（\(x<y\)），另一个长宽分别为\(a\)、\(b\)（\(a<b\)）。
因为长宽之和相同，所以\(x+y=b+a\)。因为长宽之差互为相反数，所以\(x-y+b-a=0\)。
由第二个式子得到\(x+y-y-y+b+a-a-a=0 \to x+y+b+a-2y-2a=0\)，由第一个式子得到\(x+y+x+y-2y-2a=0 \to 2x+2y-2y-2a=0 \to 2x=2a \to x=a \to x=a且y=b\)。
这时我们就可以证明两个长方形全等，又因为第二三条条件，我们得知了这两个长方形是左上角重合一个横着一个竖着的两个相同长方形。

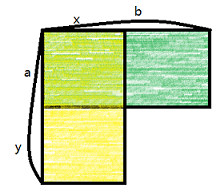
题目又给了我们长方形的长和宽，这时我们只要枚举左上角，即可确定一对满足2.3.4.5.条的友矩阵，再用二维前缀和判断和是否相等即可。

神奇的代码

#include<bits/stdc++.h>

#define int long long

using namespace std;

int n,m,a,b;
int s[1005][1005];
int qzh[1005][1005];
int ans = -1e17;

signed main(){
	
	freopen("matrix.in","r",stdin);
	freopen("matrix.out","w",stdout);
	
	cin >> n >> m >> a >> b;
	for(int i = 1;i <= n;++ i){
		for(int j = 1;j <= m;++ j){
			scanf("%lld",&s[i][j]);
			qzh[i][j] = qzh[i][j-1]+qzh[i-1][j]-qzh[i-1][j-1]+s[i][j];
		}
	}
	
	if(a < b) swap(a,b); 
	
	for(int i = 1;i+a-1 <= n;++ i){
		for(int j = 1;j+a-1 <= m;++ j){
			//以(i,j)为左上角的矩阵
			int sx = i+a-1,sy = j+b-1;
			int sums = 0;
			sums = qzh[sx][sy]-qzh[i-1][sy]-qzh[sx][j-1]+qzh[i-1][j-1];
			int hx = i+b-1,hy = j+a-1; 
			int sumh = 0;
			sumh = qzh[hx][hy]-qzh[i-1][hy]-qzh[hx][j-1]+qzh[i-1][j-1];
			if(sums == sumh){
				ans = max(ans,sums);
			}
		} 
	}
	
	if(ans != -1e17) cout << ans;
	else cout << "Chinese_zjc_ L";
	
	return 0;
	
}