2024国庆S综合强化Day1

A 四舍五入

link

求{ \(i/j\) } $ < 0.5$ ({}是取小数)，即\(i/j-\lfloor i/j \rfloor < 0.5\)，两边同时乘\(j\)，\(i-\lfloor i/j \rfloor j < 0.5j\)，会发现（别问怎么发现的）左边就是\(i\) % \(j\)，即\(i\) % \(j < 0.5j\)。观察一下图片：

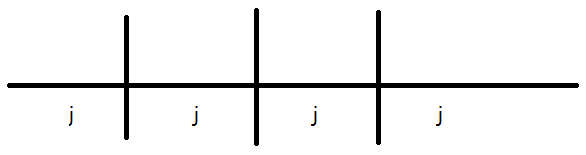
我们把序列分为许多段\(0\) ~ \(j-1\)、\(j\) ~ \(2j-1\)、\(2j\) ~ \(3j-1\)……，那么每个区间对\(j\)取模都是\(0\) ~ \(j-1\)，每个区间的前一半对答案有贡献，这样，这个序列就是对于每个\(j\)的所有\(i\)，只要枚举\(j\)即可。
对于有贡献的点，由于是一个区间，我们可以枚举每个区间，用差分来把这个区间的前一半（也是一个区间）都加一，代表这个区间的每一个\(i\)被当前的\(j\)贡献了\(1\)。
复杂的\(O(n*n/j) = O(nln_n)\)。
记得优化输入输出。

神奇的代码

#include<bits/stdc++.h>

using namespace std;

int n;
int ans[2000005];

signed main(){
	
	freopen("count.in","r",stdin);
	freopen("count.out","w",stdout);
	
	cin >> n;
	for(int j = 1;j <= n;++ j){
		for(int i = 0;i <= n;i += j){
			ans[i] += 1;
			ans[min(i+(j-1)/2+1,n+1)] -= 1;
		}
	}
	
	for(int i = 1;i <= n;++ i)
		ans[i] += ans[i-1],printf("%d ",ans[i]);
	
	return 0;
	
} 

B 填算符

link

\(O(n^2)\)（50分）做法

先不考虑第三个条件。
首先我们想一位的情况，&要求高，只有两边都是\(1\)才会保持\(1\)，而|相对来说比较好，只要两边有一个\(1\)即可力挽狂澜，所以我们认为|比&好，可以在后面救场（只要有\(1\)就救活了），所以我们初步设想答案是先\(k\)个&和再\(n-k-1\)个|组在一起会得到最优答案（可以自证一下，交换两个可以发现&在前的确好）。
现在就该考虑第三个条件了。
我们考虑把&往后移，首先我们规定这些&的位置的大小关系就是现在这样的，因为如果不同我们就可以交换一下。从最靠后的那个开始移，依次枚举这一个放在\(n\)、\(n-1\)、\(n-2\)……的位置，然后扫一下这时的整个序列，看看和最大值是否相同。相同之后，下一个就可以从这一个的位置再接着往前放，接着判断，就是循环每一个&放的位置，最后即可得到字典序最大的。
因为枚举每个&有一个\(n\)，求答案扫序列又有一个\(n\)，而枚举放在哪每次是从上次接着放的，所有&总共是\(n\)，不贡献时间复杂度，所以最终时间复杂度是\(O(n^2)\)。

神奇的代码

#include<bits/stdc++.h>

#define int long long

using namespace std;

int n,k;
int a[1000005];
int ans;
int wz[1000005];
int fh[1000005];

signed main(){
	
	freopen("bitop.in","r",stdin);
	freopen("bitop.out","w",stdout);
	
	cin >> n >> k;
	for(int i = 1;i <= n;++ i)
		cin >> a[i];
	
	ans = a[1];
	for(int i = 1;i <= k;++ i){
		ans &= a[i+1],wz[i] = i;
		fh[i] = 1;
	}
	for(int i = k+1;i < n;++ i){
		ans |= a[i+1];
		fh[i] = 0;
	}
	
	int w = n-1;
	for(int i = k;i >= 1;-- i){
		fh[i] = 0;fh[w] = 1;
		int res = ans-1;
		while(res != ans&&w > 0){
			//cout << w << " ";
			res = a[1];
			for(int j = 1;j < n;++ j){
				if(fh[j] == 1) res &= a[j+1];
				else res |= a[j+1];
			}
			if(res != ans) swap(fh[w],fh[w-1]),w--;;
		}
		wz[i] = w;
		w--;
	}
	
	for(int i = 1;i <= k;++ i)
		cout << wz[i] << " ";
	
	return 0;
	
}

\(O(n)\)（满分）做法

我们要优化掉扫序列求答案的\(n\)。