CTF 之 Crypto (Cryptography) 学习笔记

CTF 之 Crypto (Cryptography)

Chapter 0. 前置知识

群 (Group)

给定一个集合 \(G\neq \emptyset\) 以及二元代数运算 \(\circ\)，若满足：

  • 封闭性 (Closure)：\(\forall u,v\in G\)，\(u\circ v\in G\)；
  • 结合律 (Associativity)：\(\forall u,v,w\in G\)，\((u\circ v)\circ w=u\circ (v\circ w)\)；
  • 单位元 (Identity)：\(\exists e\in G\)，\(\forall u\in G\)，\(e\circ u=u\)；
  • 逆元 (Inverse)：\(\forall u\in G\)，\(\exists u^{-1}\in G\)，\(u\circ u^{-1}=e\)。

则称集合 \(G\) 对代数运算 \(\circ\) 作成一个群，记作 \((G,\circ)\)。

Ex. 正有理数集 \((\mathbb Q^+,\times)\) 对乘法作成群；实数域 \(\mathbb R\) 上的 \(m\) 阶可逆矩阵对乘法作成群（记作一般线性群 \(\text{GL}_m(\mathbb R)\)）。

半群 (Semigroup) & 幺半群 (Monoid)

  • 半群：满足封闭性、结合律；
  • 幺半群：满足封闭性、结合律、单位元。

易知，幺半群是「含有单位元」的半群，群是「每个元素皆有逆元」的幺半群。

交换群 / 阿贝尔群 (Abelian Group)

对于群 \((G,\circ)\)，若满足交换律 (Commutativity)：\(\forall u,v\in G\)，\(u\circ v=v\circ u\)，则称之为交换群 / 阿贝尔群。

Ex. 整数加法群 \((\mathbb Z,+)\) 为交换群；但 \(\text{GL}_m(\mathbb R)\) 不是交换群。

环 (Ring) & 幺环 (Ring with Identity)

给定一个集合 \(R\neq \emptyset\) 以及两个二元代数运算 \(+,\circ\)，若满足：

  • \((R,+)\) 作成交换群；
  • 结合律 (Associativity)：\(\forall u,v,w\in R\)，\((u\circ v)\circ w=u\circ (v\circ w)\)；
  • 分配律 (Distributivity)：\(\forall u,v,w\in R\)，\((u+v)\circ w=u\circ w+v\circ w\)，\(w\circ (u+v)=w\circ u+w\circ v\)。

则称集合 \(R\) 对代数运算 \(+,\circ\) 作成一个环，记作 \((R,+,\circ)\)，并通常称运算 \(+,\circ\) 为加法和乘法。

对于环 \((R,+,\circ)\)，若 \(\circ\) 满足单位元 (Identity)：\(\exists e\in G\)，\(\forall u\in G\)，\(e\circ u=u\)，则称之为幺环。

交换环 (Commutative Ring) & 除环 (Division Ring)

对于环 \((R,+,\circ)\)，若 \(\circ\) 满足交换律 (Commutativity)，则称之为交换环。

对于环 \((R,+,\circ)\)，若 \(\circ\) 满足逆元 (Inverse)：\(\forall u\in G\) 且 \(u\) 不是加法单位元，皆存在 \(u^{-1}\)，则称之为除环。

域 (Field)

对于环 \((R,+,\circ)\)，若它既是交换环，又是除环，则称之为域。

阶 (Order)

对于群 \(G\) 中元素 \(u\)，定义阶为最小的正整数 \(m\)，满足 \(u^m=\underbrace{u\circ u\circ \cdots \circ c}_{m个c}=e\)。

Ex. 群 \((\{1,-1,i,-i\},\times)\) 中，\(1\) 的阶为 \(1\)，\(-1\) 的阶为 \(2\)，\(i,-i\) 的阶均为 \(4\)。

同态 (Homomorphism)

代数系统间的同态指的是「不同代数系统间能够保持代数运算」的映射。

对于群 \((G,\circ)\) 和 \((H,*)\)，若有映射 \(\psi:G\to H\)，满足 \(\forall u,v\in G\)，有 \(\psi(u\circ v)=\psi(u)\times \psi(v)\)，则称映射 \(\psi\) 为从 \(G\) 到 \(H\) 的一个群同态。

Chapter 1. 古典密码

1.1 单表代换加密

凯撒密码 (Caesar Cipher)

密钥为 \(k\)，将明文中的每个字母循环右移 \(k\) 位。

埃特巴什码 (Atbash Cipher)

很简单，\(A\to Z\)，\(B\to Y\)，\(\cdots\)

简单替换密码 (Simple Substitution Cipher)

将 \(26\) 个字母随机映射，此时无法暴力破解，一般采用词频分析。

破解工具：https://quipqiup.com/

仿射密码 (Affine Cipher)

设定加密函数 \(E(x)=(ax+b)\pmod m\)，其中：

  • \(x\) 为明文映射对应的数字（通常为字母次序）；
  • \(a\) 和 \(m\) 互质；
  • \(m\) 为字母种数。

显然可得解密函数 \(D(x)=a^{-1}(x-b)\pmod m\)，其中 \(a^{-1}\) 为 \(\mathbb Z_m\) 群的乘法逆元。

1.2 多表代换加密

Playfair 密码 (Playfair Cipher)

流程：

  • 对于密钥，先进行去重操作，再将密钥的字母顺次填入 \(5\times 5\) 的矩阵内。剩下的空间填入未加入的 \(a\sim z\)。由于只有 \(25\) 个位置，一般将 \(q\) 去除，或将 \(i,j\) 视作同一字母。
  • 将明文每两个分为一组。若组内字母相同，将 \(x\) 添加到两个字母中央，并重新分组。若剩下一个字母，也加入 \(x\)。
  • 在每组中，找到两个字母在矩阵中的地方：
    • 若两个字母同行，取两个字母右方的字母（若在最右侧，则取最左侧的字母）；
    • 若两个字母同列，取两个字母下方的字母（若在最下侧，则取最上侧的字母）；
    • 若两个字母不同行不同列，则找到另两个字母（第一个字母对应行优先），使得四个字母形成一个长方形的四个角。

Ex. 明文为 Hide，密钥为 playfair example，则得到矩阵：

P L A Y F
I R E X M
B C D G H
K N O Q S
T U V W Z

明文分段为 HI DE，得到密文 BM OD。

Polybius 密码 / 棋盘密码 (ADFGX Cipher)

一战德军电报采用了 ADFGX 五个字母实现加密，密码表为：

A D F G X
A b t a l p
D d h o z k
F q f v s n
G g j c u x
X m r e w y

对于明文的每个字符，将其替换为它的行列对应字母。

  • 特征：密文只含 5 个字母，密文长度是明文长度的 \(2\) 倍。

Ex. 明文为 HELLO，密文为 DD XF AG AG DF。

维吉尼亚密码 (Vigenere Cipher)

维吉尼亚密码其实就是二维的凯撒密码，属于多表密码的一种简单形式。

它的密钥为串，循环拷贝至明文的长度，第 \(i\) 个字母加密明文的第 \(i\) 位字母。

Ex. 明文为 comegreatwall，密钥为 crypto。先将密钥循环拷贝：

明文 c o m e g r e a t w a l l
密钥 c r y p t o c r y p t o c

于是得到密文为 efktzferrltzn。

希尔密码 (Hill Cipher)

令 \(A=0,\cdots,Z=25\)，将明文表示为一个 \(n\) 维列向量 \(\mathrm a\)，密钥为 \(\text{key}\in \mathbb Z_{26}^{n\times n}\) 且可逆。密文即为 \(\text{key}\times \mathrm a\)。

Ex. 明文为 ACT，即 \(\begin{bmatrix}0 \\ 2 \\ 19\end{bmatrix}\)，密钥为 \(\begin{bmatrix}6 & 24 & 1 \\ 13 & 16 & 10 \\ 20 & 17 & 15\end{bmatrix}\)，则密文为 \(\begin{bmatrix}15 \\ 14 \\ 7\end{bmatrix}\)，即 POH。

1.3 其他类型加密

详见 ctf-wiki，https://ctf-wiki.org/crypto/classical/others/，较为混杂且无营养。

Chapter 2. 对称加密

2.1 伪随机数生成器（Pseudo Random Number Generator）

PRNG 是用来生成「接近于绝对随机序列」的数字序列的算法。

一般来说，PRNG 依赖一个初始值（aka. 种子），来生成对应的伪随机数数列。

随机性的严格性

  • 随机性：随机数不存在统计学偏差，是完全杂乱的数列；
  • 不可预测性：不能从过去的序列推测出下一个出现的数；
  • 不可重现性：除非数列保存下来，否则不能重现相同的数列。

三个性质的严格性依次递增。随机数分为三类：

类别 随机性 不可预测性 不可重现性
弱伪随机数 ✅ ❌ ❌
强伪随机数 ✅ ✅ ❌
真随机数 ✅ ✅ ✅

我们在密码学中使用第二种。

2.2 流密码

  • 流密码一般 逐字节 或 逐 bit 处理信息，密钥与明文的长度相同，且密钥派生自「伪随机数生成算法」。

  • 流加密都是对称加密。

线性同余生成器（Linear Congruential Generator）

\(S_0=\text{seed}\)，\(S_{n+1}=(aS_n+b) \pmod m\)。

线性反馈移位寄存器（Linear Feedback Shift Register）

一般，一个 \(n\) 级反馈移位寄存器，形如下图：

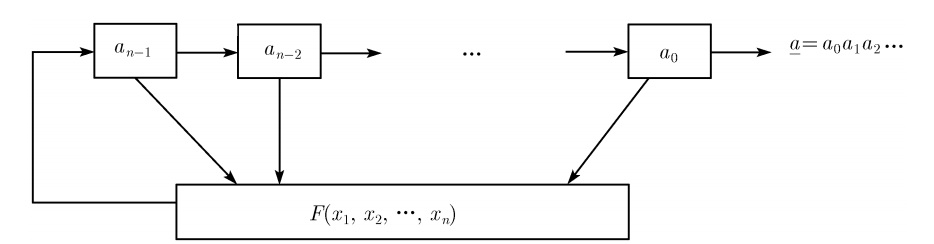
其中 \(a_0,a_1,\cdots,a_{n-1}\) 为初态，\(\mathrm{F}\) 为反馈函数，\(a_{i+n}=\mathrm{F}(a_i,a_{i+1},\cdots,a_{i+n-1})\)。

如果 \(\mathrm{F}\) 为线性函数，称其为线性反馈移位寄存器，否则称为非线性…。

【这一块我暂时还没学会，留坑】

非线性反馈移位寄存器

为了让密钥流输出的序列尽可能复杂，我们可以使用非线性反馈移位寄存器，常见的有三种：

  • 非线性组合生成器：对多个 LFSR 的输出使用一个非线性组合函数；
  • 非线性滤波生成器：对一个 LFSR 的内容使用一个非线性组合函数；
  • 钟控生成器：使用一个（或多个）LFSR 的输出来控制另一个（或多个）LFSR 的时钟。

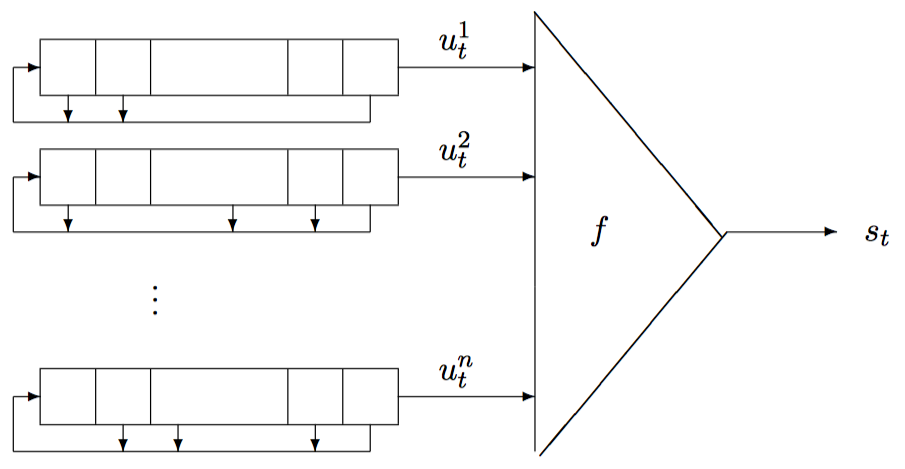
以 Geffe 为例，它包含 3 个线性反馈移位寄存器，反馈函数（非线性）为 \(F(x_1,x_2,x_3)=(x_1 \and x_2)\oplus (\urcorner x_1 \and x_3)\)。

它有一个很致命的弱点，就是 \(F\) 与 \(x_1,x_3\) 相等的概率均为 \(75\%\)。

RC 4

RC4 算法广泛应用于 SSL / TLS 协议和 WEP / WPA 协议。基本流程：

  • 初始化 \(S\) 和 \(T\) 数组。

    for i = 0 to 255 do
    S[i] = i
    T[i] = K[i mod keylen])

  • 初始化置换 \(S\)。

    j = 0
for i = 0 to 255 do 
    j = (j + S[i] + T[i]) (mod 256) 
    swap (S[i], S[j])

  • 生成密钥流。

    i = j = 0 
for each message byte b
    i = (i + 1) (mod 256)
    j = (j + S[i]) (mod 256)
    swap(S[i], S[j])
    t = (S[i] + S[j]) (mod 256) 
    print S[t]

2.3 块密码

posted @ 2025-01-08 19:50  wlzhouzhuan  阅读(568)  评论(0)    收藏  举报