01背包

01背包

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

示例1：

​
输入：n = 3, w = 4, weight = [1, 3, 4], value = [15, 20, 30]
输出：35
​

解题思路

经典动态规划问题。

二维数组解法

1. 确定dp数组以及其下标的含义

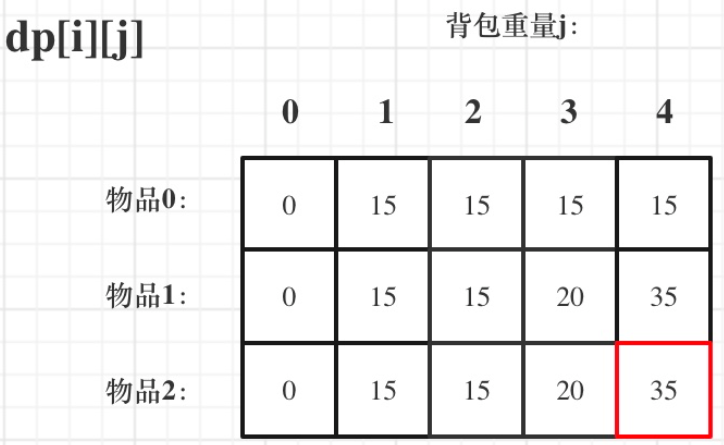
   dp[i,j]表示任取下标为0-i的物品(物品的下标从0开始)放入容量为j的背包中，可以获得的最大价值总和

2. 确定递推公式

   • 如果装不下当前物品，那么装 前i个物品所得的最大价值 和 前i-1个物品所得的最大价值 是一样的。即有 dp[i][j] = dp[i-1][j]

   • 如果装得下当前物品：

     • 假设1：选择不装当前物品，那么装 前i个物品所得的最大价值 和 前i-1个物品所得的最大价值 是一样的。即有 dp[i][j] = dp[i-1][j]。

     • 假设2：选择将当前物品装入背包，那么找出在背包容量为j - weight[i]时装入前i-1个物品时所得的最大价值，再加上当前物品i的价值就是dp[i][j]。

     选取假设1和假设2中的 较大价值 作为当前的总价值即可。即dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])

3. dp数组的初始化

   首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。

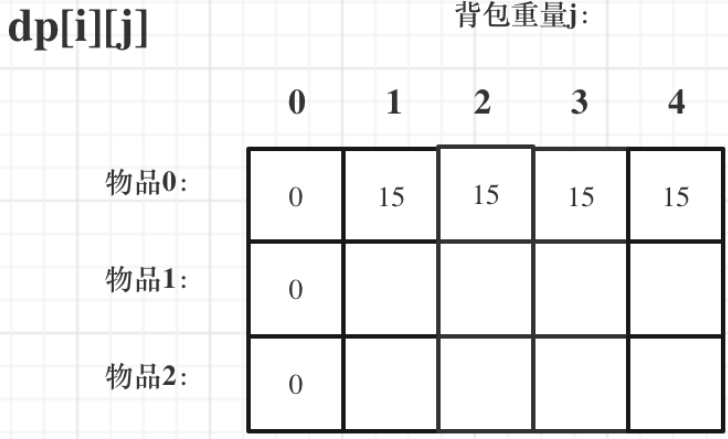
   再看其他情况。状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i是由i-1推导出来，那么i为0的时候就一定要初始化。

   dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

   那么很明显当j < weight[0]的时候，dp[0][j]=0，因为背包容量比编号0的物品重量还小。

   当j >= weight[0]时，dp[0][j]应该是value[0]，因为背包容量放足够放编号0物品。

   按照示例一，可以得到的初始后的dp数组如下所示。

   

   另外，由递推公式可以看出dp[i][j]（除dp[0][j]和 dp[i][0]）是由左上方数值推导出来了，那么 其他下标初始为什么数值都可以，因为都会被覆盖（一般都赋值为0）。

4. 确定遍历顺序

   先遍历物品或者先遍历背包都可以，但一般选择先遍历物品(这样好理解)

5. 举例推导dp数组

    

C++

//二维数组
class Solution {
public:
    void backpack(vector<int> weight, vector<int> value, int bagsize) {
        //1. dp[i][j]表示任取下标为0-i的物品(物品的下标从0开始)放入容量为j的背包中，可以获得的最大价值总和
        vector<vector<int>> dp(weight.size(),vector<int>(bagsize + 1,0));
        //3. 初始化dp数组
//        for (int i = 0; i < weight.size(); i++) { //这一步初始可以省略，因为dp数组全部赋值为0了
//            dp[i][0] = 0;
//        }
        for (int j = weight[0]; j < bagsize + 1; j++) {
            dp[0][j] = value[0];
        }
        //4. 遍历顺序(先遍历物品或者先遍历背包都可以)，此处选择先遍历物品
        for (int i = 1; i < weight.size(); i++) { //遍历物品
            for (int j = 0; j < bagsize + 1; j++) { //遍历背包容量
                //2. 状态方程
                if (j < weight[i]) dp[i][j] = dp[i - 1][j];
                else
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
        //5. 打印dp方程组
        for (int i = 0; i < weight.size(); i++) {
            for (int j = 0; j < bagsize + 1; j++) {
                cout << dp[i][j] << " ";
            }
            cout << endl;
        }
        cout << "The maximum value a backpack can get is " << dp[weight.size() - 1][bagsize];
    }
};

JavaScript

/**
 * @param {number[]} weight
 * @param {number[]} value
 * @param {number} bagsize
 */
// 二维数组
function backpack(weight, value, bagsize) {
    // 1.dp[i][j]表示为任取下标为0-i的物品放到容量为j的背包中可以获得的最大价值总和
    const dp = new Array(weight.length).fill().map(item => Array(bagsize + 1).fill(0));
    // 3.dp的初始化
    for (let j = weight[0]; j < bagsize + 1; j++) {
        dp[0][j] = value[0];
    }
    //4.遍历顺序
    for (let i = 1; i < weight.length; i++) {
        for (let j = 0; j < bagsize + 1; j++) {
            //2.状态方程
            if (j < weight[i]) dp[i][j] = dp[i - 1][j];
            else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
        }
    }
    //5.打印dp数组
    console.log(dp);
};

一维数组解法

1. 确定dp数组以及其下标的含义

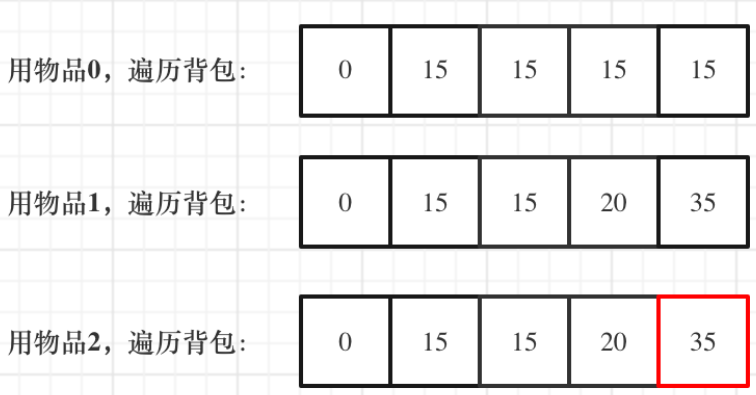
   dp[j]dp[j]表示容量为j的背包，可以获得的最大价值总和

2. 确定递推公式

   dp[j]可以通过 dp[j - weight[j]]推导出来，dp[j - weight[i]]表示容量为 j - weight[i]的背包所得的最大价值。

   dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。

   所以此时dp[j]有两个选择，一个是取自己dp[j]，一个是取dp[j - weight[i]] + value[i]，在这二者中取价值较大的即可。

   即dp[j] = max(dp[j], dp[j-weight[i]]+value[i])

3. dp数组的初始化

   dp[0] = 0（背包容量为0）。因为背包问题中的物品价值都为正整数，必须保证取到最大值，所以其余的dp[j]也都初始化为0

4. 确定遍历顺序

   只能先遍历物品，再遍历背包。 注意这种方式背包的遍历顺序是不一样的，要从大往小遍历。

5. 举例推导dp数组

   

C++

//一维数组
class Solution1 {
public:
    void backpack(vector<int> weight, vector<int> value, int bagsize) {
        //1. dp[j]表示容量为j的背包，可以获得的最大价值总和
        vector<int> dp(bagsize + 1, 0);
        //3. 初始化dp数组,dp[0] = 0（背包容量为0）。因为背包问题中的物品价值都为正整数，必须保证取到最大值，所以其余的dp[j]也都初始化为0
        //4. 遍历顺序，必须先遍历物品，因为一维滚动数组的值相当于按层来保留了前一层数组的值，
        // 并且再更新数组时，要从后向前更新，因为后面的数组会用到前一层保留下来的值
        for (int i = 0; i < weight.size(); i++) { // 物品的下标从0开始
            for (int j = bagsize; j >= 0; j--) {
                //2. 状态方程
                if (j >= weight[i]) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        //5. 打印dp方程组
        for (int j = 0; j <= bagsize; j++) {
            cout << dp[j] << " ";
        }
        cout << endl;
        cout << "The maximum value a backpack can get is " << dp[bagsize];
    }
};

JavaScript

/**
 * @param {number[]} weight
 * @param {number[]} value
 * @param {number} bagsize
 */
// 一维数组
function backpack1(weight, value, bagsize) {
    // 1.dp[j]表示容量为j的背包可以获得的最大价值总和
    const dp = new Array(bagsize + 1).fill(0);
    // 3.dp的初始化
    //4.遍历顺序,先遍历物品
    for (let i = 0; i < weight.length; i++) {
        for (let j = bagsize; j >= weight[i]; j--) {
            //2.状态方程
            dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    //5.打印dp数组
    console.log(dp);
};