Contraint Satisfaction Problems 约束满足问题
1 CSP定义
1.1 什么是约束满足问题
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. ——Wikipedia
约束满足问题 (Constraint satisfaction problem,CSPs) 是定义为一组对象的数学问题,其状态必须满足许多约束或限制。
约束满足问题包含一组变量和一组变量间的约束,解决此类问题需要找到所有变量的一个(或多个)赋值,使所有约束都得到满足。
例如,地图着色问题是一个典型的约束满足问题,要求给地图上的每个区域分配一种颜色,使得相邻的区域颜色不同。
有关概念
约束问题的组成
一个约束满足问题由 变量集合\(X\)、值域集合\(D\)和约束集合\(C\)组成三个部分组成。
值域集合中的值域\(D_i\)由变量\(X_i\)的可能取值组成。
约束集合中的每个约束\(C_i\)由一个有序对\(<scope,relation>\)组成。\(scope\)这个约束中的变量组,\(relation\)则是这些变量取值应该满足的关系。
简单来说:
一个约束满足问题就是要给一些变量分配一些值,但是要满足一些条件。这些变量、值和条件有三个名字:
- 变量集合\(X\):就是要分配值的变量的名单,比如\(X_1,X_2,...,X_n\)。
- 值域集合\(D\):就是每个变量可以取的值的范围,比如\(D_1,D_2,...,D_n\)。每个变量\(X_i\)只能从它对应的值域\(D_i\)里面选一个值。
- 约束集合\(C\):就是一些规则,限制了变量之间的关系,比如\(C_1,C_2,...,C_m\)。每个规则\(C_i\)包含两部分:一部分是说这个规则涉及哪些变量,叫做\(scope\);另一部分是说这些变量的值要满足什么样的关系,叫做\(relation\)。
状态与赋值
在约束满足问题中,状态是一组变量的赋值,即\(X=\{X1,X2,…,Xn\}\),其中\(X_i\)是\(D_i\)中的一个值。初始状态是空的赋值,即\(X=\{\}\)。后继函数是给一个未赋值的变量分配一个值,即\(X=\{…,X_i=d_i,…\}\)。目标测试是检查当前的赋值是否满足所有的约束,即\(C={C_1,C_2,…,C_m}\)。如果满足,则找到了问题的解。
1.2 举例:地图着色问题
这个问题的目标是给澳大利亚地图上的不同区域涂上不同的颜色,并且要求相邻的区域不能有相同的颜色。
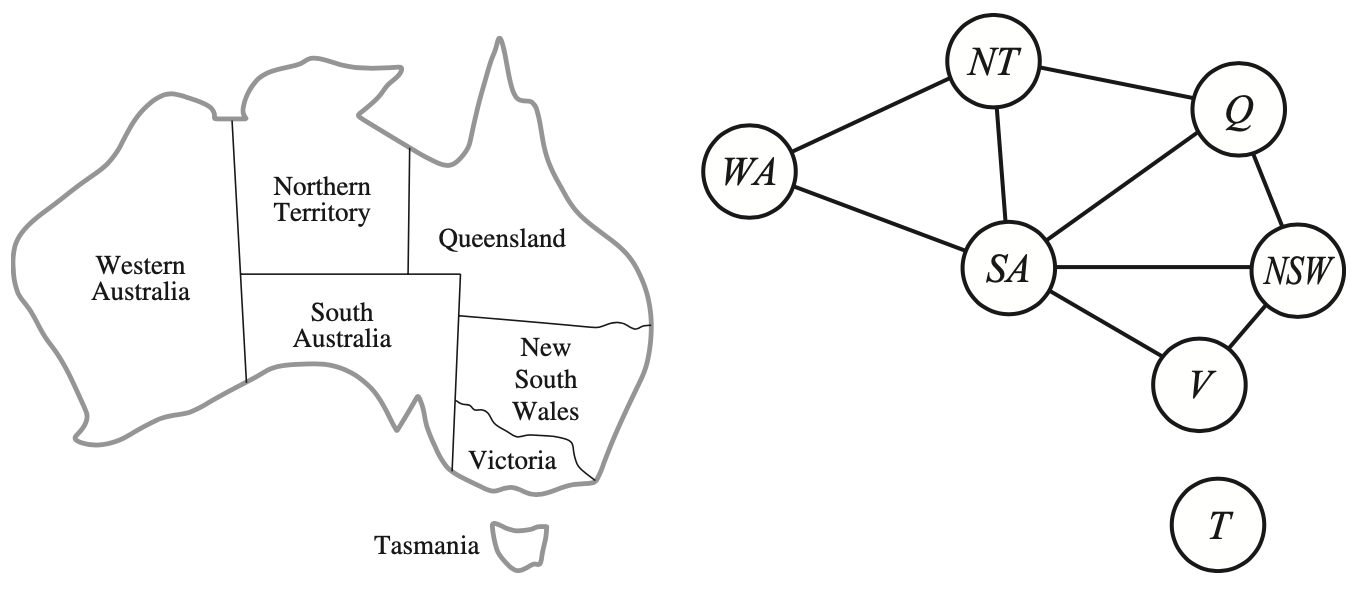
这个问题可以用以下三个部分来描述:
- 变量集合\(X\):就是地图上的各个区域,比如澳大利亚地图的例子中,有\(X=\{WA,NT,Q,NSW,V,SA,T\}\),分别代表西澳大利亚、北领地、昆士兰、新南威尔士、维多利亚、南澳大利亚和塔斯马尼亚。
- 值域集合\(D\):就是可以用来涂色的颜色,比如\(D=\{红,绿,蓝\}\)。
- 约束集合\(C\):就是规定相邻区域不能有相同颜色的条件,比如\(C=\{WA\neq NT ,WA\neq SA,NT\neq Q,NT\neq SA\neqQ\neq NSW\neq,Q\neq SA,NSW\neq V,NSW\neq SA ,V\neq SA\}\),其中\(\neq\)表示不等于。
这个问题的一个可能的解是:
{\(WA=红\),\(NT=绿\),\(Q=红\),\(NSW=绿\),\(V=红\),\(SA=蓝\),\(T=绿\)}
如下图所示:
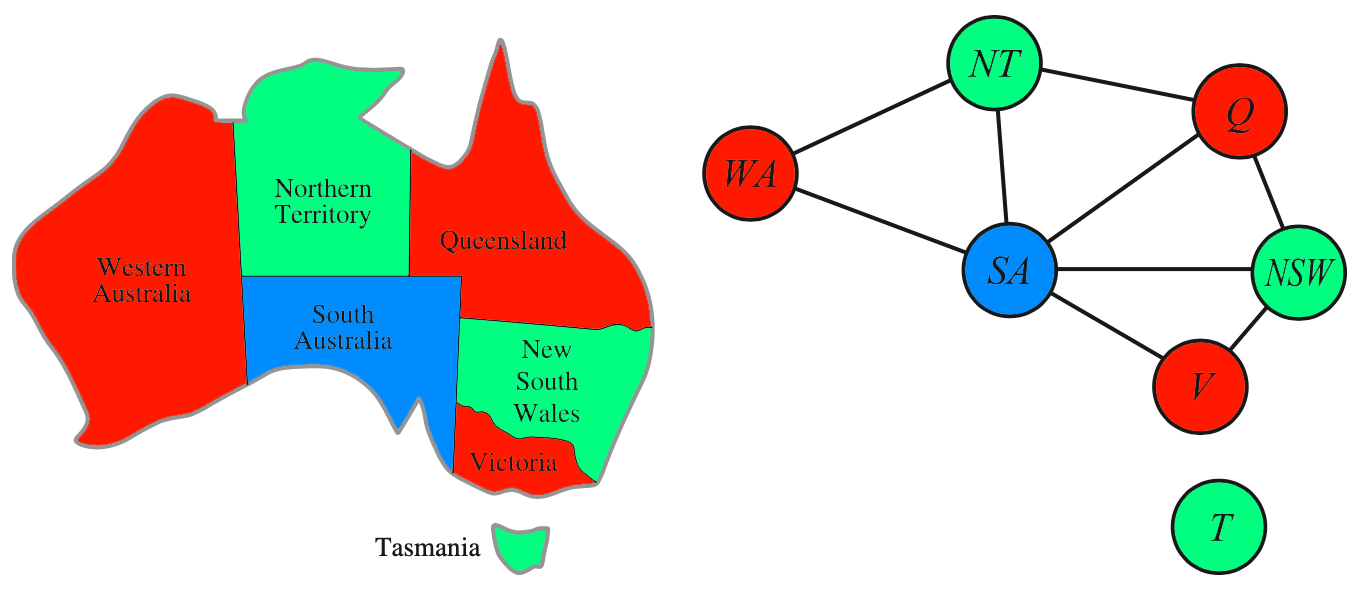
1.3 形式化的约束满足问题
1.3.1 值域
CSP涉及的变量可以是有限的或无限的。
例如,数独问题中的变量就是有限值域的,而整数集合或字符串集合则是无限的。
变量可以是离散的,也可以是连续的。
例如,地图着色问题中的变量是离散的,而天文观测的时间则是连续的。
线性规划问题是最著名的一类连续值域CSP问题。
1.3.2 约束
CSP涉及的约束可以是一元的、二元的、高阶的或全局的。
一元约束是最简单的约束类型,它只限制单个变量的取值。
例如,在一个户外活动的安排问题中,阿鲲不喜欢打篮球,可以这样表示:\(<(阿鲲),阿鲲\neq 打篮球>\)
二元约束与两个变量有关。
例如,阿鲲参加的活动要和阿娇不同,可以这样表示:\(阿鲲\neq 阿娇\)
全局约束是变量个数任意的约束。
最常见的全局约束是\(Alldiff\),指约束中所有变量必须取不同的值。
在数独游戏中(见第 6.2.6 节),一行或一列中的所有变量必须满足\(Alldiff\)约束。
二元约束可以用约束图来表示,如前文地图着色问题中的右图。
前面所讲的约束都是绝对约束,必须严格满足的等式约束和不等式,违反绝对约束的解是不可接受的。
而现实生活中的CSP问题含有偏好约束。偏好约束是指达到此目标值时允许发生正或负偏差,将约束条件右端项视为追求的目标值,偏好约束指出哪些解是更偏好的。
例如,在一个教务处排课问题中,李老师偏好在下午上课。把李老师安排在上午上课也是问题的一个解,但这不是最优的解。
有约束偏好的CSP问题可以用基于路径的或局部的最优搜索方法求解,这样的问题被称为约束优化问题(COP问题)。
2 约束传播:CSP中的推理
在常规的状态空间搜索中,算法通过搜索寻找从初始状态到目标状态的路径。
在CSP问题中,约束传播是一种特殊的推理方法,它使用约束来减少变量的合法取值范围,从而影响到跟此变量有约束关系的另一个变量的取值,如此进行。
约束传播的核心思想是局部相容性,具体有以下几种类型:
- 结点相容:如果单个变量值域中的所有取值满足它的一元约束,就称此变量是结点相容的。
- 弧相容:如果CSP中某个变量值域中的所有取值满足该变量的所有二元约束,则称此变量是弧相容的。
- 路径相容:如果两个变量的集合对于第三个变量是相容的,指的是对这两个变量的每一个相容的赋值,第三个变量都有合适的取值同时使得三个变量之间都是相容的。
- K相容: 如果对于任何k-1个变量的赋值,第k个变量总能被赋予一个和前面k-1个变量相容的值。
如果一个图是k相容的,k-1相容的,…,直到1相容的,那么此CSP是强k相容的。 - 边界相容:变量的取值必须同时满足与其他约束条件的限制和变量自身的边界限制。
3 CSP回溯搜索
3.1 定义
回溯法是一种可以找出所有(或一部分)解的一般性算法,尤其适用于约束满足问题(在解决约束满足问题时,我们逐步构造更多的候选解,并且在确定某一部分候选解不可能补全成正确解之后放弃继续搜索这个部分候选解本身及其可以拓展出的子候选解,转而测试其他的部分候选解)。
3.2 思想
回溯法采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现,现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。
回溯法通常用最简单的递归方法来实现。
3.3 大致过程
(1) 确定当前的问题的目标以及约束条件;
(2) 在未赋值的变量中选择一个进行赋值。可以直接按顺序依次选择,也可以使用启发式方法去选择最优变量;
(3) 对于未赋值的变量,我们应当根据约束条件去确定变量可以取的值;
(4) 在可选择的值里面选择一个填入。填入完成后根据选择的顺序来选择下一个需要进行赋值的未赋值变量;
(5) 对于未赋值变量,若任意一个数值填入均不符合约束变量,则表明了前面的过程中填入的数值有误。
此时应当先回溯到上一个格子尝试填入符合约束条件的变量。如果所有的数字都已经尝试过了,仍然无法找到合法的填充方案,就会回溯到上上个格子,以此类推,直到找到合法的解或者搜索完所有的可能性。
(6) 当算法结束的时候,我们会输出找到的最终解。若完成全部回溯后没有没有符合约束条件的解,那么我们便会报告无解。
3.4 算法分析
算法在最坏的情况下,需要搜索整个解空间,时间复杂度为指数级别,即\(O(b^d)\),\(b\)是每个变量的取值范围,\(d\)是变量的数量。不过,在实际的应用中,回溯法通常能够在搜索树的较浅层找到合法解,因此实际运行时间会受到变量选择和值域约束等因素的影响。
4 CSP局部搜索
4.1 定义
局部搜索算法对求解许多CSP都是很有效的。它们使用完整状态的形式化:初始状态是给每个变量都赋一个值,搜索过程是一次改变一个变量的取值。如最小冲突启发法便是采用了该思想。
4.2 组成部分
(1) 初始解的生成:从可行解空间中随机生成一个初始解,或者使用其他方法生成一个较优的初始解。
(2) 邻域操作:定义一些变量的值的变化方式,用于生成新的解。常见的邻域操作包括交换、替换、插入等。
(3) 评估函数:用于评估当前解的质量。通常是在CSP问题中定义的约束函数,表示解中变量的取值是否满足约束条件。
4.3 常用基本算法:最小冲突算法
4.3.1 算法定义:
最小冲突算法(Minimum Conflicts Algorithm,MCA):这是一种启发式算法,它从当前解开始,迭代地尝试调整变量的取值,以最小化当前解中的冲突数量。
4.3.2 大致过程:
给定一个约束满足问题的所有变量的初始值分配,该算法从一组变量中随机选择一个变量,其冲突违反了一个或多个约束。然后,它将最小化冲突次数的值分配给该变量。如果存在多个具有最小冲突数的值,它会随机选择一个。迭代随机变量选择和最小冲突值分配的过程,直到找到解决方案或达到预选的最大迭代次数。
4.3.3 算法分析
我们选择了从第一行开始直到最后一行,逐个处理的方法。如果这样一轮下来没有终止,就再来一轮……直到终止。
在该方法中,计算每行最小冲突的位置是这个算法比较核心的一步。简单的想法就是对每个位置,遍历所有的皇后,看看与其中几个有冲突;对N个可能的位置都执行这一操作,这就是\(O(N^2)\)的复杂度,这样每一轮的调整就是\(O(N^3)\)。
4.3.4 举例:数独问题
4.3.4.1 问题描述:
根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫(3*3)内的数字均含1-9,不重复。
4.3.4.2 解决方法:
(1). 初始为一个9x9的数独盘面。
(2). 随机选择一个空白格子作为冲突变量,在这个格子中队数字1到9分贝进行尝试。将当前情况下无冲突的对应的数字填入其中。若存在多个值符合条件,则先任选一个填入。
(3). 找到棋盘中剩余的空白格子,重复操作2。若存在一格子对任意一个数字均存在冲突,则表明上一过程中填入的数字有误,应当进行更换。同时,该空格直接填入冲突最小的值,而不需要上一步修改完成后再次进行重复计算,
(4). 重复上述的过程(3)与(4)。如果达到了预定的迭代次数或其他停止条件,则返回当前棋盘即为最优解。
4.3.4.3 图示:
最小冲突算法(MCA)解决数独问题
初始状态:
| 6 | 9 | 4 | 2 | |||||
|---|---|---|---|---|---|---|---|---|
| 4 | 6 | |||||||
| 8 | 6 | |||||||
| 3 | 1 | 5 | 7 | 2 | ||||
| 9 | 3 | 5 | ||||||
| 6 | 7 | |||||||
| 3 | 1 | 7 | ||||||
| 9 | 1 | |||||||
| 6 |
现在,我们选定第一行第二个空白格子为第一个填入数字的格子。通过分析可以得到,该格子可以填入5,7,8。我们先选择5作为我们第一次填入的数据。则得到的数组如下:
| 6 | 5* | 9 | 4 | 2 | ||||
|---|---|---|---|---|---|---|---|---|
| 4 | 6 | |||||||
| 8 | 6 | |||||||
| 3 | 1 | 5 | 7 | 2 | ||||
| 9 | 3 | 5 | ||||||
| 6 | 7 | |||||||
| 3 | 1 | 7 | ||||||
| 9 | 1 | |||||||
| 6 |
我们刚刚填入的格子中的右侧空白格子为第二个填入数字的格子。通过分析可以得到,该格子可以填入1,7,8。我们先选择1作为我们本次填入的数据。则得到的数组如下:
| 6 | 5 | 1* | 9 | 4 | 2 | |||
|---|---|---|---|---|---|---|---|---|
| 4 | 6 | |||||||
| 8 | 6 | |||||||
| 3 | 1 | 5 | 7 | 2 | ||||
| 9 | 3 | 5 | ||||||
| 6 | 7 | |||||||
| 3 | 1 | 7 | ||||||
| 9 | 1 | |||||||
| 6 |
我们再次选定其右侧空白格子为本次填入的格子。经过分析我们会发现,该格子填入1-9任一数字都存在冲突。这表明了我们上一步填入的数字有误。但是,该格子填入数字1的时候冲突最小,则该格子直接填入1。对于上一步中的空格得到的错误数据,我们再返回进行修改。
| 6 | 5 | 7* | 1* | 9 | 4 | 2 | ||
|---|---|---|---|---|---|---|---|---|
| 4 | 6 | |||||||
| 8 | 6 | |||||||
| 3 | 1 | 5 | 7 | 2 | ||||
| 9 | 3 | 5 | ||||||
| 6 | 7 | |||||||
| 3 | 1 | 7 | ||||||
| 9 | 1 | |||||||
| 6 |
重复上述的过程,我们最终便会得到最终的答案为
| 6 | 5 | 3 | 1 | 7 | 9 | 8 | 4 | 2 |
|---|---|---|---|---|---|---|---|---|
| 1 | 8 | 4 | 5 | 3 | 2 | 7 | 6 | 9 |
| 2 | 7 | 9 | 4 | 8 | 6 | 1 | 1 | 5 |
| 3 | 1 | 5 | 7 | 2 | 8 | 4 | 6 | 9 |
| 7 | 9 | 6 | 3 | 1 | 4 | 2 | 5 | |
| 8 | 4 | 2 | 9 | 6 | 5 | 1 | 7 | 3 |
| 4 | 3 | 8 | 6 | 5 | 1 | 9 | 2 | 7 |
| 9 | 6 | 7 | 2 | 4 | 3 | 5 | 8 | 1 |
| 5 | 2 | 1 | 8 | 9 | 7 | 6 | 3 | 4 |
5 两种算法的比较
原理不同:
回溯法是一种基于深度优先搜索的算法,通过枚举所有可能的解来求解问题;而MCA是一种基于启发式搜索的算法,通过局部搜索和最小冲突策略来快速求解问题。
时间复杂度不同:
回溯法在求解数独问题时,需要枚举所有可能的解,当环境较差的时候。时间复杂度为指数级别;而MCA的时间复杂度相对较低,通常在\(O(n^3)\)到\(O(n^4)\)之间。
实现方式:
回溯法通常使用递归函数来实现,可以比较容易地处理各种复杂的情况;而MCA则需要实现局部搜索和最小冲突策略,相对不宜读懂且实现更为困难。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号