博客作业01-抽象数据类型

1.用ADT的抽象数据模型描述你的有理数数据类型。

ADT  Rational{
	数据对象：D={T1[2],T2[2],T3[2]|T1[0],T[1]为有理数T1的分子和分母
							  T2[0],T2[1]为有理数T2的分子和分母
							  T3[0],T3[1]为有理数T3的分子和分母}
基本关系：R1={<T1,T2>,<T2,T3>}
基本操作：
  	Rationals(T1,T2,T3,A)
	add(T1,T2,T3)
	minuss(T1,T2,T3)
	multiply(T1,T2,T3)
	divide(T1,T2,T3)
	modify(T3,e,i)
        destroy(T1)
        destroy(T2)
        destroy(T3)
}ADT  Rational

2.数据结构、函数说明

• 

3.代码实现说明

(1)构造三个数组存放有理数T1，T2，T3

• 
  做法：动态申请内存，把结构体数组的分母，分子分别给数组T1，T2进行赋值

(2)有理数相加

• 
  做法：首先先考虑分母相同的情况，分子直接相加，分母等于T1的分母，值赋予数组T3,再进行约分输出
  再考虑分母不相同的情况，T3的分子T[1]等于T1的分子T1[0]乘以T2的分母T2[1]加上T1的分母T1[1]乘以T2的分子T2[0]，T3的分母T3[1]等于T1的分母T1[1]乘以T2的分母T2[1]，接着约分后输出

(3)有理数相减

• 
  做法：首先考虑分母相同的情况，T3的分子T3[0]等于T1的分子T1[0]减去T2的分子T2[0]，T3的分母T3[0]等于T1的分母T1[1]，如果值为0，输出0，否则约分输出
  再考虑分母不同的情况，T3的分母T3[0]等于T1的分母T1[1]乘以T2的分母T2[1]，T3的分子T3[0]等于T1的分子T1[0]乘以T2的分母T2[1]减去T1的分母T1[11]乘以T2的分子T2[0]，接着约分后输出

(4)有理数相乘

• 
  做法：T3的分子T3[0]等于T1的分子T1[0]乘以T2的分子T2[0]，T3的分母T3[0]等于T1的分母T1[1]乘以T2的分母T2[1]，接着约分后输出

(5)有理数相减

• 
  做法：T3的分子T3[0]等于T1的分子T1[0]乘以T2的分母T2[1]，T3的分母等于T2的分子T2[0]乘以T1的分母T1[1]，接着约分后输出

(6)求最大公约数进行约分

• 
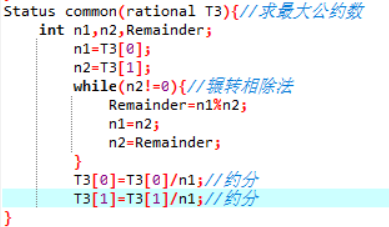
  做法：利用辗转相除法求最大公约数，最大公约数存于变量n1，最后利用n1进行T3分子T3[0]和T3分母T3[1]的约分

(7)释放空间

• 
  做法：运用free()函数销毁T1，T2，T3数组

(8)使用引用类型参数e修改有理数T3的分子和分母

• 
  做法：主函数里定义整型变量e,函数定义使用&进行引用，利用cin输入对e进行赋值，再利用参数i和e对T3的分子T3[0]和分母T3[1]赋值

4.代码互评

• 我选取的是熊志坚同学的代码

1.函数设计风格不同：

• 我的代码ｃ和ｃ＋＋并用，志坚的代码都是ｃ＋＋，看出他对ｃ＋＋还是挺熟练的，我需要向他学习
  

2.变量名命名不同：

志坚：

我：

3.结构体

• 我有结构体，志坚没有使用结构体,他的方法比较节省空间
  我:
  志坚:无

4.函数

• 定义函数时，我定义的形参T3是指针，调用函数时需要传入地址，志坚同学定义函数的形参T3不是指针，举加法函数(其他函数都一样)为例
  我：
  志坚：

5：输出展示

• 我：输出有理数为0时，我直接输出0
  

• 志坚：输出有理数为0时，不直接输出0
  

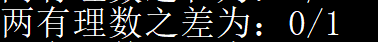
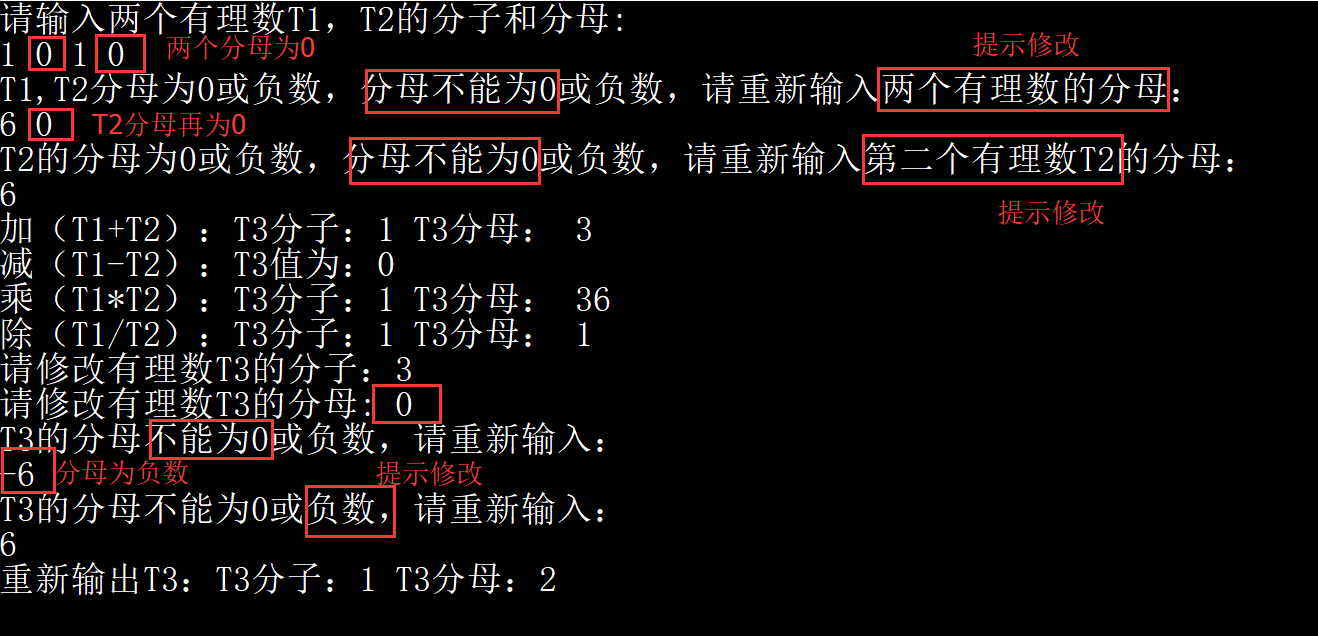
5.结果展示

• 正常运行情况：
  
  
• 极端：
  

6.总结

• 数据结构：数据元素之间存在一种或者多种关系,高效率地处理好数据元素的关系，有利于读码人的理解，也有助于后期代码的修改与完善。(个人观点)
• 抽象数据类型：类似于数学模型的构造：先定义数学模型，再对数学模型里的各个成员进行操作，写出能实现相应功能的函数，最后再拼装成型。(个人观点)