CSP11
CSP11
T1
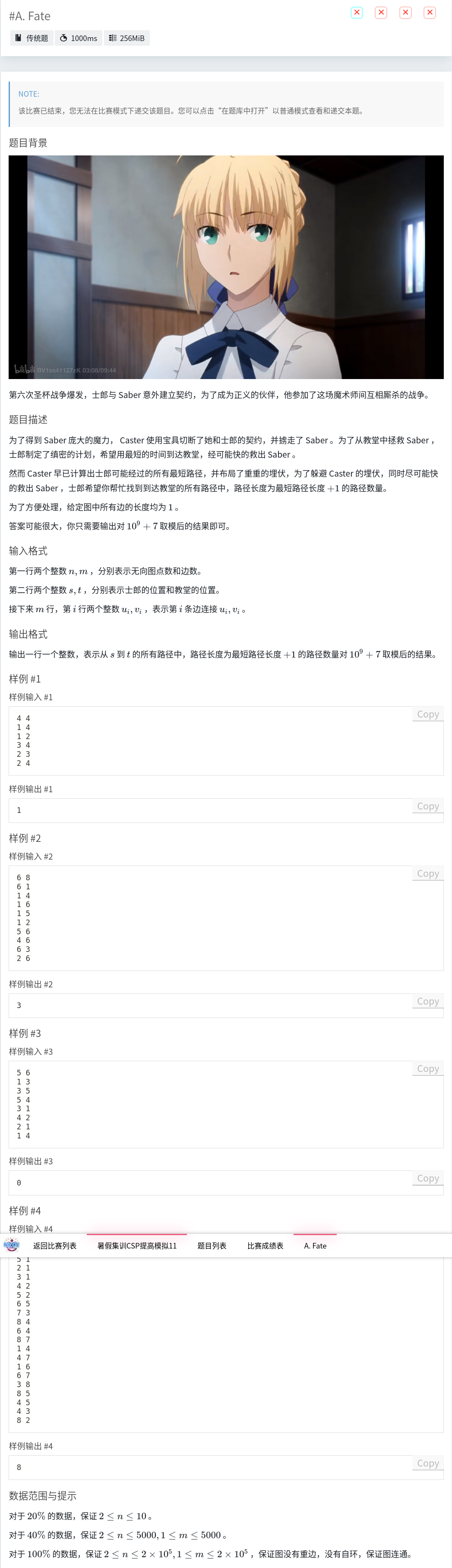
暴力
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
// #pragma comment(linker, ¡°/STACK:512000000,512000000¡±)
using namespace std;
const int N = 2e5+5,mod=1e9+7,inf=1e9;
int n,m,dis[N];bool vis[N];
vector <int> edge[N];
struct Node
{
int dis,u;
bool operator < (const Node& A)const
{
return dis>A.dis;
}
};
int st,en;
void dij(int st)
{
for(int i=1;i<=n;i++)dis[i]=1e9;
priority_queue <Node> q;
q.push({0,st});
dis[st]=0;
while(q.size())
{
int u=q.top().u;q.pop();
if(vis[u])continue;
vis[u]=1;
for(auto to:edge[u])
{
if(vis[to])continue;
if(dis[to]>dis[u]+1)
{
dis[to]=dis[u]+1;
q.push({dis[to],to});
}
}
}
}
inline ll dfs(const int u,const int step,const int tg)
{
if(step>tg||(step==tg&&u!=en))return 0;//这两个特判优化不少
if(u==en)return step==tg;
vis[u]=1;
ll res=0;
for(auto to:edge[u])
{
if(vis[to])continue;
res=(dfs(to,step+1,tg)+res)%mod;
}
vis[u]=0;
return res;
}
int main()
{
speed();
// freopen("Fate1.in","r",stdin);
// freopen("Fate9.in","r",stdin);
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
cin>>n>>m;
cin>>st>>en;
// cout<<"**********"<<endl;
int u,v;
for(int i=1;i<=m;i++)
{
cin>>u>>v;
edge[u].pb(v);edge[v].pb(u);
}
dij(st);
memset(vis,0,sizeof vis);
int tg=dis[en]+1;
cout<<dfs(st,0,tg);
return 0;
}
我们其实没必要\(dfs\)找一遍,其实可以直接\(BFS\),从起点开始,\(f\)表示最短路径的数量,\(g\)表示最短路径+1的数量
如何转移?,设当前为\(u->to\),\(dis_u==dis_{to}则g_{u}+=f_{to}\)\(dis_{to}=dis_u+1,则g_{to}+=g_u,f_{to}+=f_u\)
注意顺序一定不能换,否则\(g_u\)不上
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
#define pii pair<int,int>
// #pragma comment(linker, ¡°/STACK:512000000,512000000¡±)
using namespace std;
const int N = 2e5+5,mod=1e9+7,inf=1e9;
int n,m,dis[N],g[N],f[N],id[N];bool vis[N];
vector <int> edge[N];
vector <pii> G;
struct Node
{
int dis,u;
bool operator < (const Node& A)const
{
return dis>A.dis;
}
};
int st,en;
void dij(int st)
{
for(int i=1;i<=n;i++)dis[i]=1e9;
priority_queue <Node> q;
q.push({0,st});
dis[st]=0;
while(q.size())
{
int u=q.top().u;q.pop();
if(vis[u])continue;
vis[u]=1;
for(auto to:edge[u])
{
if(vis[to])continue;
if(dis[to]>dis[u]+1)
{
dis[to]=dis[u]+1;
q.push({dis[to],to});
}
}
}
}
// unordered_map <int,map<int,int>> dp;
// inline ll dfs(const int u,const int step,const int tg)
// {
// if(step>tg||(step==tg&&u!=en))return 0;
// if(u==en)return step==tg;
// if(dp[u][step])return dp[u][step];
// // cout<<step<<endl;
// vis[u]=1;
// ll res=0;
// for(auto to:edge[u])
// {
// if(vis[to])continue;
// res=(dfs(to,step+1,tg)+res)%mod;
// }
// vis[u]=0;
// return dp[u][step]=res;
// }
int main()
{
speed();
// freopen("Fate1.in","r",stdin);
// freopen("Fate9.in","r",stdin);
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
cin>>n>>m;
cin>>st>>en;
// cout<<"**********"<<endl;
int u,v;G.pb({0,0});
for(int i=1;i<=m;i++)
{
cin>>u>>v;
G.pb({u,v});
edge[u].pb(v);edge[v].pb(u);
}
dij(st);
memset(vis,0,sizeof vis);
auto ans=[&](int st,int en)
{
queue <int> q;
q.push(st);
f[st]=1;
// vis[st]=1;
while(q.size())
{
int u=q.front();q.pop();
// if(vis[u])continue;
// vis[u]=1;
for(auto to:edge[u])
{
if(dis[u]==dis[to])
{
g[u]+=f[to];g[u]%=mod;
// q.push(to);
}
}
for(auto to:edge[u])
{
if(dis[to]==dis[u]+1)
{
g[to]+=g[u];
f[to]+=f[u];
g[to]%=mod;f[to]%=mod;
if(!vis[to])vis[to]=1,q.push(to);
}
}
}
return g[en];
};
ll p=ans(st,en);
cout<<p<<endl;
return 0;
}
T2
暴力
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e4+5;
int sum[N];
int n,a;
struct Fs
{
int x,w,v;
double dis;
}f[N];
bool cmp(Fs a,Fs b)
{
return a.x<b.x;
}
bool cmpdis(Fs a,Fs b)
{
return a.dis<b.dis;
}
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
// freopen("EVA1.in","r",stdin);
cin>>n>>a;
bool ev=1;
for(int i=1;i<=n;i++)
{
cin>>f[i].w>>f[i].x>>f[i].v;
if(i>1&&f[i].v!=f[1].v)ev=0;
}
if(ev)
{
// cout<<"****"<<endl;
sort(f+1,f+1+n,cmp);
for(int i=1;i<=n;i++)sum[f[i].x]+=f[i].w;
for(int i=1;i<=f[n].x;i++)sum[i]+=sum[i-1];
int ans=0;
for(int i=1;i<=f[n].x;i++)
{
ans=max(ans,sum[min(i+a,f[n].x)]-sum[i-1]);
}
cout<<ans<<endl;
return 0;
}
// for(int i=1;i<=n;i++)
// cout<<"****"<<endl;
int ans=0;
for(double t=0.0001;t<=1;t+=0.0001)
{
for(int i=1;i<=n;i++)
{
f[i].dis=f[i].x+f[i].v*t;
}
sort(f+1,f+1+n,cmpdis);
for(int i=1;i<=n;i++)sum[i]=sum[i-1]+f[i].w;
int st=1;
for(int i=1;i<=n;i=-~i)
{
while(f[i].dis-a>f[st].dis)st++;
ans=max(ans,sum[i]-sum[st-1]);
}
}
for(double t=0.001;t<=10;t+=0.02)
{
for(int i=1;i<=n;i++)
{
f[i].dis=f[i].x+f[i].v*t;
}
sort(f+1,f+1+n,cmpdis);
for(int i=1;i<=n;i=-~i)sum[i]=sum[i-1]+f[i].w;
int st=1;
for(int i=1;i<=n;i=-~i)
{
while(f[i].dis-a>f[st].dis)st++;
ans=max(ans,sum[i]-sum[st-1]);
}
}
cout<<ans;
return 0;
}
/*
3 10
1 15 55
10 20 55
100 25 55
*/
正解是枚举每一条鱼,设为\(i\)作为左端点(一定是最优的),通过相对速度,算出每一条鱼对它的贡献\(l_t,r_t\),进行差分即可
一些细节问题,
精度问题
还有判断\(r\)是负数的情况不能要
速度相等的情况要注意
由于精度问题\(l,r\)可能要互换位置,先要换位置,再判断是否\(r<0\)
关于差分时,右端点\(r\)要加上一个\(eps\),就是为了先让鱼进来,再让鱼出去,以满足答案最优
点击查看代码
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e4+5;
const double eps=1e-9;
int sum[N];
int n,a,cnt[N],jcnt[N];
struct Fs
{
int x,w,v;
}f[N];
bool cmp(Fs a,Fs b)
{
return a.x<b.x;
}
map <double,int> tmm;
int main()
{
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
// freopen("EVA1.in","r",stdin);
cin>>n>>a;
for(int i=1;i<=n;i++)
{
cin>>f[i].w>>f[i].x>>f[i].v;
}
sort(f+1,f+1+n,cmp);ll ans=0;
for(int i=1;i<=n;i++)
{
tmm.clear();
ll res=f[i].w;
for(int j=1;j<=n;j++)
{
if(i==j)continue;
if(f[j].v==f[i].v)
{
if(f[j].x>=f[i].x&&f[j].x-f[i].x<=a)res+=f[j].w;
// cout<<res<<endl;
continue;
}
// if(f[j].x<f[i].x&&f[j].v<=f[i].v)continue;
double l=1.0*(f[i].x-f[j].x)/(f[j].v-f[i].v);
double r=1.0*(f[i].x-f[j].x+a)/(f[j].v-f[i].v);
// cout<<t<<" "<<r<<rdl;
// if(t<0)continue;
if(l>r-eps)swap(l,r);//先要换位置,再判断是否r<0
if(r<0)continue;
l=max(l,0.0000);
tmm[l]+=f[j].w;
tmm[r+eps]-=f[j].w;
// if(f[j].x>f[i].x&&f[j].v>=f[i].v&&f[j].x-f[i].x>a)continue;
}
ans=max(ans,res);
for(auto it:tmm)
{
res+=(it.second);
ans=max(ans,res);
}
}
cout<<ans;
return 0;
}
/*
3 10
1 15 55
10 20 55
100 25 55
*/
T3
计数题
做法一:
排序\(a\)数组,然后,我们初始左右指针\(l=1,r=n\),在满足\(l<r企鹅a[l]+a[r]>=k\)的情况下不断让\(r\)指针右移,这样,一定会有一个边界,使得左端点\(a_l\)只能与\([r,n]\)的\(a\)匹配,我们把他们加入到数列中,用\(ans\)乘上贡献,类似插空的思想,当前未放入\(a_l,a_r\),
数列中已经包含\([1,l-1],[r+1,n]\),这样就有\(n-r+l-1+1\)个空,再减去有\([1,l-1]\)元素周围不能放\(a_r,a_l\)所以,贡献为\(n-r+l-2\times (l-1)\),但是要注意最后还用相同数的情况,所以乘上相同数阶乘的逆元即可
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
#define endl '\n'
//#define int long long
#define pb push_back
// #pragma comment(linker, ¡°/STACK:512000000,512000000¡±)
using namespace std;
const int N = 2e5+5,mod=998244353,inf=1e9;
ll n,k,a[N],jie[N];
ll qpow(ll a,ll b)
{
ll ans=1;
while(b)
{
if(b&1)ans=ans*a%mod;
b>>=1;
a=a*a%mod;
}
return ans;
}
ll calc(ll l,ll r)
{
return (n-l-r+2);
}
int main()
{
speed();
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
cin>>n>>k;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
jie[0]=1;
for(ll i=1;i<=n;i++)jie[i]=jie[i-1]*i%mod;
sort(a+1,a+1+n);
ll l=1,r=n;
ll ans=1;
while(l<=r)
{
while(l<r&&a[r]+a[l]>=k)
{
ans=ans*calc(l,r)%mod;
r--;
}
ans=ans*calc(l,r)%mod;
l++;
}
ll cnt=1;
a[n+1]=inf;
for(int i=2;i<=n+1;i++)
{
if(a[i]==a[i-1])cnt++;
else
{
ans=ans*qpow(jie[cnt],mod-2)%mod;
cnt=1;
}
}
cout<<ans<<endl;
// for()
return 0;
}
T4
暴力
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
// #pragma comment(linker, “/STACK:512000000,512000000”)
using namespace std;
const int N = 1e5+5,mod=998244353,inf=1e9;
int n,m,q,a[N];
vector <int> edge[N];
int dep[N],f[N][25],kd;
int dis[N];
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1;
f[u][0]=fa;
for(int i=1;i<=20;i++)
f[u][i]=f[f[u][i-1]][i-1];
for(auto to:edge[u])
{
if(to==fa)continue;
dfs(to,u);
}
}
ll ans;
bool vis[N];
inline int lca(int x,int y)
{
if(dep[x]<dep[y])swap(x,y);
for(int i=20;i>=0;i--)
{
if(dep[f[x][i]]>=dep[y])x=f[x][i];
}
if(x==y)return x;
for(int i=20;i>=0;i--)
{
if(f[x][i]!=f[y][i])x=f[x][i],y=f[y][i];
}
return f[x][0];
}
int main()
{
speed();
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
cin>>n>>m>>q;
int u,v;
bool lian=1;
for(int i=1;i<=n-1;i++)
{
cin>>u>>v;
if(abs(u-v)!=1)lian=0;
edge[u].pb(v);edge[v].pb(u);
}
for(int i=1;i<=m;i++)
{
cin>>a[i];
}
dfs(1,0);
int l,r;
while(q--)
{
cin>>l>>r;
if(l==r)
{
cout<<1<<endl;
continue;
}else if(lian)
{
int mi=1e9,mx=0;
for(int i=l;i<=r;i=-~i)
{
mx=max(mx,dep[a[i]]);
mi=min(mi,dep[a[i]]);
}
cout<<mx-mi+1<<endl;
continue;
}
for(int i=1;i<=n;i=-~i)vis[i]&=0;
for(int i=l;i<=r;i=-~i)
{
if(vis[a[i]])continue;
for(int j=i+1;j<=r;j=-~j)
{
if(vis[a[j]])continue;
int q=lca(a[i],a[j]);
vis[a[i]]=vis[a[j]]=1;
if(!vis[q])
{
vis[q]=1;
}
int x=a[i],y=a[j];
while(x!=q)
{
x=f[x][0];
vis[x]=1;
}
while(y!=q)
{
y=f[y][0];
vis[y]=1;
}
}
}
ll ans=0;
for(int i=1;i<=n;i=-~i)
{
// if(vis[i])cout<<i<<" ";
ans+=(vis[i]==1);
}
// cout<<endl;
cout<<ans<<endl;
}
return 0;
}
/*
10 9 3
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
1 2 3 4 5 6 7 8 9
1 4
4 7
2 9
*/
回滚莫队做法(逆天题库给的限制甚至连暴力分都不如)
逆天\(LCA O(nlogn)\)预处理\(O(1)\)查询,用\(ST\)表维护(否则挂一个\(log\)),这个还是理性用吧,当调用\(LCA\)的次数很少,这种写法是要命的
有个显然的结论,将所有关键点按 DFS 序排序,走过的边的数量为排序后相邻的点之间的距离。记走过的边的数量为 \(cnt\),则此时这些关键点所构成的虚树的大小为\(cnt/2+1\)
利用了\(dfn\)的性质,假设有\(dfs序为\)\(i,j,k,w(i<j<k<w)\)三个点,则\(dis(i,j)+dis(j,k)+dis(k,w)+dis(i,w)+2=2*ans\),(为什么还有\(dis(i,w)\)?,因为这玩意首尾还要连一下)推广规律\(有k个点,他们之间的答案即为各点之间的距离/2+1\),这样的话我们只用维护一个点的前驱和后继即可,,然后考虑用回滚莫队,用链表维护
发现只删的前驱后继可以用链表维护,套一个只删不加的回滚莫队,右端点从右到左排序,左端点从左到右排序,同时用 \(O(1) lca\) 求两个点间的距离,用的是 \(dfs\) 序 \(lca\),这样常数小,还不用多记一个欧拉序。我们相当于固定一个点\(r=k\),然后让初始化从一个块开始的答案,然后回滚就行了
点击查看代码
#include <bits/stdc++.h>
#define speed() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define ll long long
#define ull unsigned long long
#define lid (rt<<1)
#define rid (rt<<1|1)
// #define endl '\n'
//#define int long long
#define pb push_back
#define pii pair<int,int>
using namespace std;
const int N = 1e5+5;
int n,k,qu,a[N];
vector <int> edge[N];
int dep[N],dfn[N],rk[N];int dfstot;
int lg[N],st[20][N],f[N][20];
inline void dfs(int u,int fa){
dep[u]=dep[fa]+1;
dfn[u]=++dfstot;rk[dfstot]=u;
st[0][dfstot]=fa;
for(int v:edge[u]) if(v!=fa) dfs(v,u);
}
inline int Min(int x,int y){return dep[x]<dep[y]?x:y;}
inline void init(){
for(int i=2;i<=n;i++) lg[i]=lg[i>>1]+1;
for(int j=1;j<=19;j++) for(int i=1;i<=dfstot-(1<<j)+1;i++) st[j][i]=Min(st[j-1][i],st[j-1][i+(1<<(j-1))]);
}
inline int lca(int l,int r){//这里的LCA求的dfs序的LCA对应返回的是dfs序对应的点下标
if(l==r) return rk[l];
if(l>r) swap(l,r);
++l;int k=lg[r-l+1];
return Min(st[k][l],st[k][r-(1<<k)+1]);
}
struct query
{
int l,r,bl,id;
inline bool operator < (const query &x)const{return bl!=x.bl?l<x.l:r>x.r;}
}q[N];
struct Node
{
int pre,nxt,id;
Node(){}
Node(int p,int n,int id):pre(p),nxt(n),id(id){}
};
vector <Node> s;
int dis(int x,int y){return dep[rk[x]]+dep[rk[y]]-2*dep[lca(x,y)];}
int pre[N],nxt[N],num[N];
ll res=0;
inline void Del(int x)
{
--num[x];
if(!num[x])
{
res-=dis(pre[x],x)+dis(x,nxt[x]);
res+=dis(pre[x],nxt[x]);
// cout<<res<<endl;
pre[nxt[x]]=pre[x];nxt[pre[x]]=nxt[x];
}
}
inline void del(int x)
{
s.pb({pre[x],nxt[x],x});
--num[x];
if(!num[x])
{
res-=dis(pre[x],x)+dis(x,nxt[x]);
res+=dis(pre[x],nxt[x]);
pre[nxt[x]]=pre[x];nxt[pre[x]]=nxt[x];
}
}
int len,ans[N];
inline void solve()
{
int l=1,r=0;
for(int i=1;i<=qu;i++)
{
if(q[i].bl!=q[i-1].bl)//不同块内初始化
{
memset(num,0,sizeof num);
for(int j=(q[i].bl-1)*len+1;j<=k;j++)++num[dfn[a[j]]];
int lst=0;
for(int j=1;j<=n;j++)//找前驱
{
pre[j]=lst;
if(num[j])lst=j;
}
for(int j=1;j<=n;j++)if(!pre[j])pre[j]=lst;//因为首尾要相连
lst=0;
for(int j=n;j;j--)//找后继
{
nxt[j]=lst;
if(num[j])lst=j;
}
for(int j=n;j;j--)if(!nxt[j])nxt[j]=lst;//因为首尾要相连
res=0;
for(int j=1;j<=n;j++)if(num[j])res+=dis(pre[j],j);//统计答案
r=k;
}
l=(q[i].bl-1)*len+1;//紧接着上面初始化完成
while(r>q[i].r)Del(dfn[a[r--]]);
int now=res;
while(l<q[i].l)del(dfn[a[l++]]);
// cout<<res<<endl;
ans[q[i].id]=res/2+1;
res=now;
while(s.size())
{
Node tmp=s.back();s.pop_back();
if(!num[tmp.id])nxt[tmp.pre]=tmp.id,pre[tmp.nxt]=tmp.id;
++num[tmp.id];
}
}
}
bool M2;
int main()
{
speed();
// freopen("in.in","r",stdin);
// freopen("out.out","w",stdout);
cin>>n>>k>>qu;
len=sqrt(k);
int u,v;
for(int i=1;i<=n-1;i++)
{
cin>>u>>v;edge[u].push_back(v);edge[v].push_back(u);
}
dfs(1,0);init();
for(int i=1;i<=k;i++)cin>>a[i];
for(int i=1;i<=qu;i++){cin>>q[i].l>>q[i].r,q[i].bl=(q[i].l-1)/len+1,q[i].id=i;}
sort(q+1,q+1+qu);
solve();
for(int i=1;i<=qu;i++)cout<<ans[i]<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号