Matlab函数linprog笔记。

所谓线性规划问题，是指在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。

一般线性规划问题的数学模型为：

 

 

 

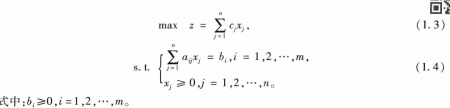
可行解：满足约束条件式（1.4）的解x=[x1,...,xn]^T，称为线性规划问题的可行解，而使目标函数式（1.3）达到最大值的可行解称为最优解。

可行域：所有可行解构成的集合称为问题的可行域，记为R。

 

而在matlab中，线性规划的标准形式为：

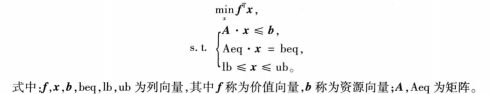
Matlab中求解线性规划问题的命令为linprog，官方文档：https://ww2.mathworks.cn/help/optim/ug/linprog.html

在《数学建模算法与应用》中着重介绍的是[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)

其中，x为返回决策向量的取值；favl返回目标函数的最优质的；f为价值向量；A和b对应线性不等式约束；Aeq和beq对应线性等式的约束；lb和ub分别对应决策向量的下界向量和上界向量。

而使用时，可使用

[x,fval]=linprog(f,A,b)

[x,fval]=linprog(f,A,b,Aeq,beq)

[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)

 

当没有线性不等式，只有线性等式的约束使，可以这样用：[x,fval]=linprog(f,[],[],Aeq,beq,lb,ub)，即A和b取[]

 

PS：如果求的是最小值，则f，A，b，Aeq，beq，lb和up均取负号即可。