迭代法求解方程（组）的根

 

 

摘自福星师哥的博客在这里给出链接https://blog.csdn.net/Akatsuki__Itachi/article/details/80719686

 

首先，迭代法解方程的实质是按照下列步骤构造一个序列x0,x1,…,xn,来逐步逼近方程f(x)=0的解:

1）选取适当的初值x0；

2）确定迭代格式，即建立迭代关系，需要将方程f(x)=0改写为x=φ(x)的等价形式；

3)   构造序列x0，x1，……，xn，即先求得x1=φ(x0)，再求x2=φ(x1)，……如此反复迭代，就得到一个数列x0， x1，……，xn，若这个数列收敛，即存在极值，且函数 φ(x)连续，则很容易得到这个极限值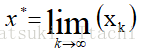,x*就是方程f(x)=0的根。

 

举个例子：

求解方程： f(x) =x^3-x-1=0  在区间 （1，1.5）内的根。

首先我们将方程写成这种形式：

用初始根x0=1.5带入右端，可以得到

这时，x0和x1的值相差比较大，所以我们要继续迭代求解，将x1再带入公式得

直到我们我们得到的解的序列收敛，即存在极值的时候，迭代结束。

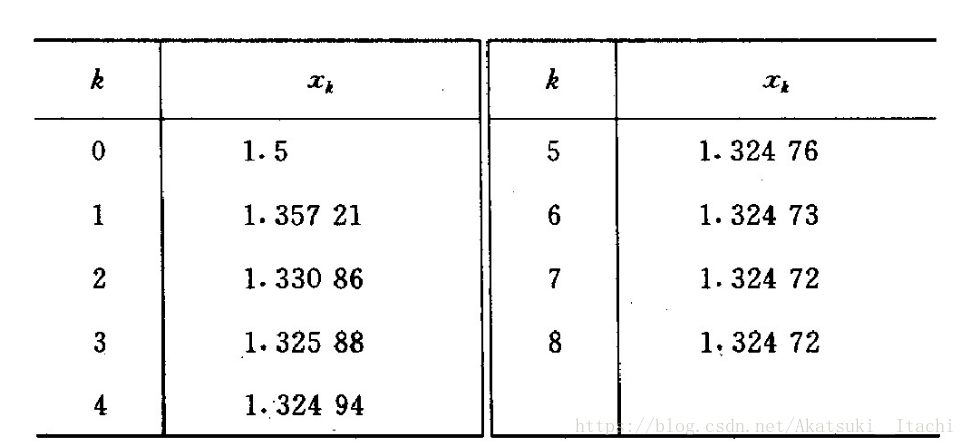
下面是这个方程迭代的次数以及每次xi的解（i=0,1,2....）

 

我们发现当k=7和8的时候，方程的解已经不再发生变化了，这时候我们就得到了此方程的近似解。

 

#define eps 1e-8
int main()
{
    x0=初始近似根；
    do{
        x1=x0;
        x0=g(x1); //按特定的方程计算新的近似根
    }while(fabs(x0-x1)>eps);
    printf("方程的近似根是%f\n",x0);
}

 

注意：如果方程无解，算法求出的近似根序列就不会收敛，那么迭代过程就会变成死循环。因此，在使用迭代算法前应先考察方程是否有解，并在算法中对迭代次数给予限制。

 

下面再写一个求解方程组的例子加深一下理解：

 

算法说明：

方程组解的初值X=（x0，x1，…，xn-1）,迭代关系方程组为：xi=gi(X)(i=0,1,…,n-1),w为解的精度,maxn为迭代次数。

算法如下：

算法核心：

int main()
{
    for (i=0; i<n; i++)
        x[i]=初始近似根;
    do
    {
        k=k+1;
        for(i=0; i<n; i++）
            y[i]=x[i];
        for(i=0; i<n; i++)
            x[i]=gi(X);   //按特定的方程计算新的近似根
        c=0;
        for(i=0; i<n; i++)
            c=c+fabs(y[i]-x[i]);//c要每次重新设初值为0
    }while(c>eps and k<maxn );
    for(i=0; i<n; i++)
        print("变量的近似根是"，x[i]);
}

 

选取初始向量 

精确度为1e-8，迭代次数为100

求解代码如下：

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define eps 1e-8
using namespace std;
const int maxn=100;
double x[10],y[10];
int main()
{
    for(int i=1;i<=4;i++)
        x[i]=0;
    int cnt=0;
    double c=0;
    do{
        for(int i=1;i<=4;i++)
            y[i]=x[i];
        for(int i=1;i<=4;i++)
        {
            x[1]=(6+x[2]-2*x[3])/10;
            x[2]=(25+x[1]+x[3]-3*x[4])/11;
            x[3]=(-11-2*x[1]+x[2]+x[4])/10;
            x[4]=(15-3*x[2]+x[3])/8;
        }
        c=0;
        for(int i=1;i<=4;i++)
            c+=(fabs(y[i]-x[i]));
    }while(c>eps&&cnt<maxn);
    for(int i=1;i<=4;i++)
        printf("x%d = %.4lf\n",i,x[i]);
}

 

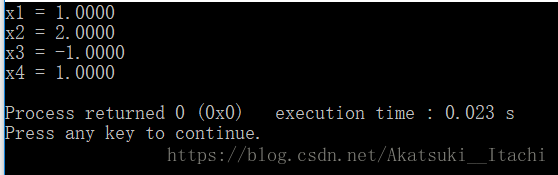
运行结果如下：

 

迭代法求解方程的过程是多样化的，比如二分逼近法求解，牛顿迭代法等。

下面就是效率比较高且比较常用的牛顿迭代法：

牛顿迭代法又称为切线法，它比一般的迭代法有更高的收敛速度，如下图所示。

首先, 选择一个接近函数f(x)零点的x0, 计算相应的f(x0)和切线斜率f'(x0)（这里f '  表示函数f的导数）。然后我们计算穿过点   (x0,f (x0))且斜率为f '(x0)的直线方程

和x轴的交点的x的坐标，也就是求如下方程的解

将新求得交点的x坐标命名为x1。如图4所示，通常x1会比x0更接近方程f(x) = 0的解。接下来用x1开始下一轮迭代 .

迭代公式可化简为：

上式就是有名的牛顿迭代公式。已经证明, 如果f'  是连续的, 并且待求的零点x是孤立的, 那么在零点x周围存在一个区域, 只要初始值x0位于这个邻近区域内, 那么牛顿法必定收敛。

 

求形如ax^3+bx^2+cx+d=0方程根的算法，系数a、b、c、d的值依次为1、2、3、4，由主函数输入。求x在1附近的一个实根。求出根后由主函数输出。

 

由以上的公式可得到代码：

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define eps 1e-8
using namespace std;
int main()
{
    double a,b,c,d;
    cin>>a>>b>>c>>d;
    double x1=1,x,f,fx;
    do{
        x=x1;
        f=((a*x+b)*x+c)*x+d;
        fx=(3*a*x+2*b)*x+c;
        x1=x-f/fx;
    }while(fabs(x1-x)>=eps);
    printf("%.2lf",x1);
}

结果如下：

 

接下来说一下二分逼近法

用二分法求解方程f(x)=0根的前提条件是：f(x)在求解的区间[a,b]上是连续的，且已知f(a)与f(b)异号，即 f(a)*f(b)<0。

令[a0,b0]=[a,b]，c0=(a0+b0)/2，若f(c0)=0，则c0为方程f(x)=0的根；否则，若f(a0)与f(c0)异号，即 f(a0)*f(c0)<0，则令[a1,b1]=[a0,c0]；若f(b0)与f(c0)异号，即 f(b0)*f(c0)<0，则令[a1,b1]=[c0,b0]。

 依此做下去，当发现f(cn)=0时，或区间[an,bn]足够小，比如| an-bn |<0.0001时，就认为找到了方程的根。

 

例：

用二分法求一元非线性方程f(x)= x^3/2+2x^2-8=0（其中^表示幂运算）在区间[0，2]上的近似实根r，精确到0.0001.

算法如下：

 

int main( )
{
    double x,x1=0,x2=2,f1,f2,f;
    print(“input a,b (f(a)*f(b)<0)”);
    input(a,b);
    f1=x1*x1*x1/2+2*x1*x1-8;
    f2=x2*x2*x2/2+2*x2*x2-8;
    if(f1*f2>0)
    {
        printf("No root");
        return;
    }
    do{
        x=(x1+x2)/2;
        f=x*x*x/2+2*x*x-8;
        if(f=0)
            break;
        if(f1*f>0.0)
        {
            x1=x;
            f1=x1*x1*x1/2+2*x1*x1-8;
        }
        else
            x2=x;
    }
    while(fabs(f)>=1e-4);
    print("root=",x);
}