《文章翻译》PCA&SVD
Principle Component Analysis && Singular Value Decomposition
强烈推荐,理解PCA和SVD很有帮助
一. Intuition of PCA
1.1 去掉多余的特征
假设我们有房子的这些信息:价格(千美元)、面积、层数、户型。
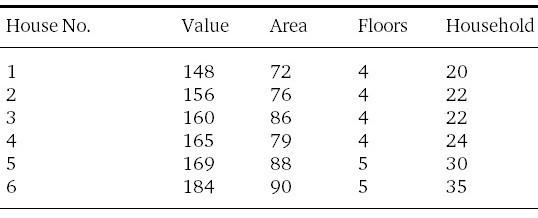
房子包含了四维的信息,我们无法在一幅图像中直观的显示出来。然而,如果你仔细的观察特征之间的联系,你将会注意到不是所有的特征都是同等重要的。
例如,你可以通过房子的层数去识别房子的价格(或对应哪个房子)吗?房子的层数是否帮助我们区分是哪个房子?房子的层数几乎相同,他们的方差很小,\(\sigma^2=0.2\) 所以房子的层数不是非常有用。那房子的户型呢?他们值变化也不是很大,但是他们的方差却很大,\(\sigma^2=127\),因此房子的户型可以很好的区别是哪个房子。
因此我们可以做一些事尽量的发掘特征,在不损失精度的情况下。目前,我们学习了各自的特征。那特征之间的相互联系是什么?如果你仔细看了上图1-1的特征,你会发现房子的价格粗略的等于房子面积的两倍。这是非常有用的信息,我们可以使用其中一个特征来取代代替另一个特征。这样两个特征之间的联系称为协方差。协方差越大,表明特征之间的相关性越强,也就是数据的冗余性很大。因此可以进行降维处理。
从之前的讨论可以明显的看出:
- 特征高方差是好事,代表更多的信息
- 特征之间高协方差是坏事,表明特征之间很多冗余
这就是PCA的目的:使得每个特征的方差都很大,使得特征之间的协方差都很小。当前我们无法用眼睛直观的感受,下文会详细描述。
1.2 魔幻展示
我们对PCA女士进行了一个简单采访-:
记者:请问您认为最完美的数据是什么样的?
PCA:下图所示
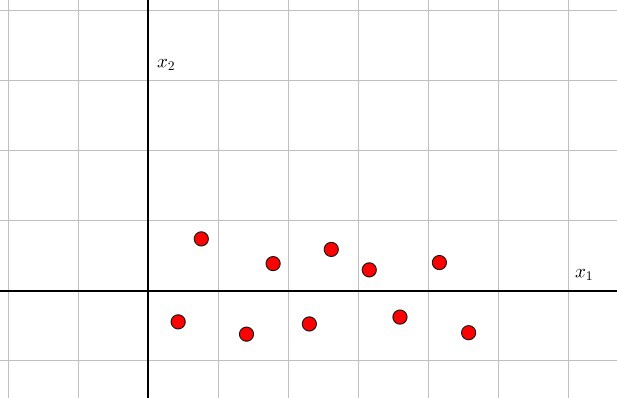
这意味着-----数据可以降低到一个维度上。观测:\(x_1\)方向的方差比\(x_2\)方向的方差大很多,也就等于去除\(x_2\)方向的数据,不会破坏很多的数据信息。此外,\(x_1\)方向的数据是递增的,完全没有依靠\(x_2\)的数据,也就等于\(x_1/x_2\)的协方差很小。为什么PCA会觉得这样的数据很完美,因为她只需进行这样的操作:
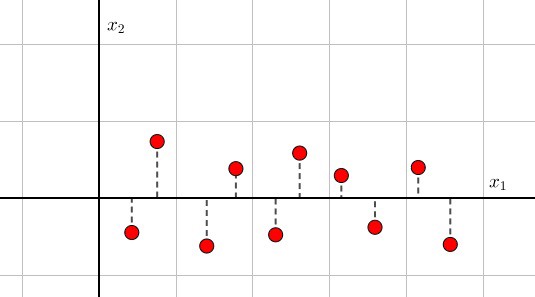
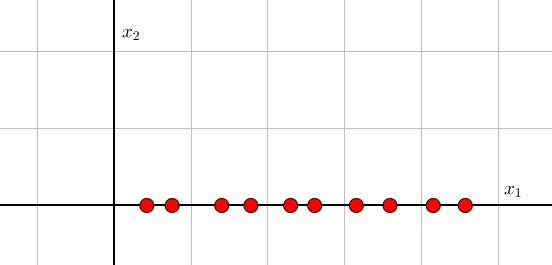
明白怎么进行的处理很重要,\(x_1\)的数据比\(x_2\)的数据更重要,所以我们去除\(x_2\)的数据。也可以表达为,把数据像\(x_1\)进行投影。二维数据使用一维数据代替。
1.3 难例图解
记者:那您觉得什么的数据不是很完美呢?数据像什么样子?
PCA:每个东西都是完美的,只要你进行一些变换即可。像下面这幅图一样:
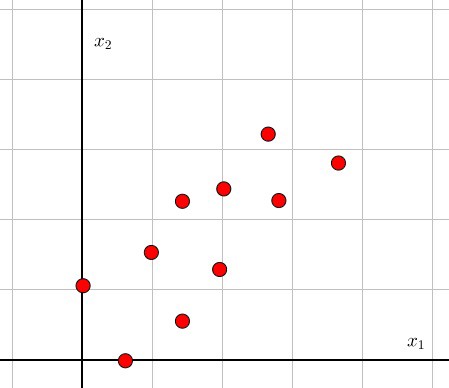
PCA:上面的图有点困难,你觉得呢?尝试将头转动一下
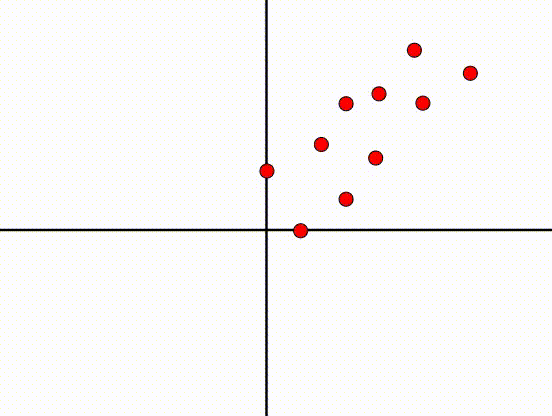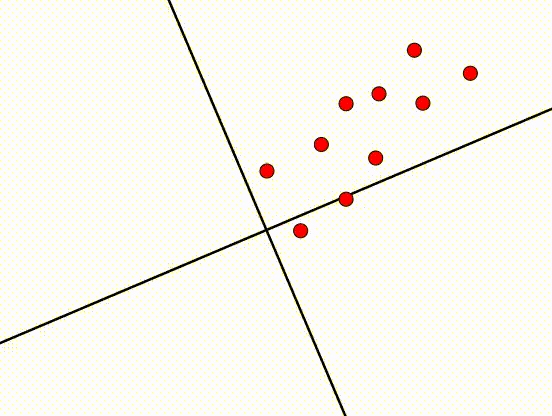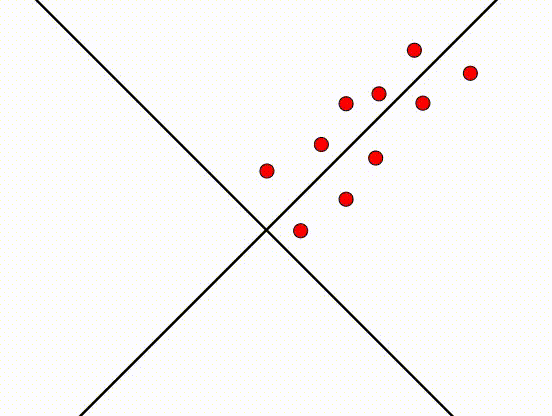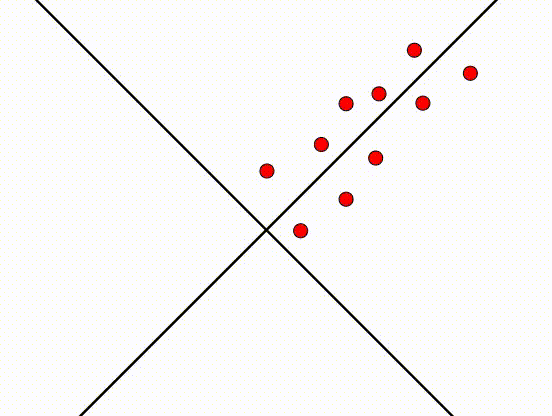
将图转动45°之后,现在的图也是将近完美的。这发生了什么事?PCA尝试找到一个轴,这个轴的方差越大越好。我们之前说\(x_1\)的特征,指的是在\(x_1\)方向的特征。然后,在旋转之后,\(x_1\)的特征代表的意义变了,不再是之前\(x_1\)方向的特征,具体含义不再重要(代表之前\(x_1\)和\(x_2\)线性联合的特征)。因为旋转了45°,所以新轴和旧轴之间的关系是:\(x_2=x_1\) 或 \(x_1-x_2=0\),新的轴设为\(z_1/z_2\):
新的轴\(z_1/z_2\)代表了数据的主要成分(principle component),转换之后,数据和之前的数据基本一样,方差和协方差也类似。
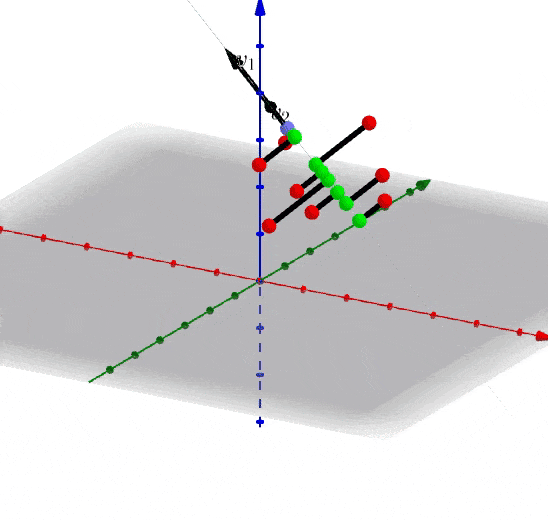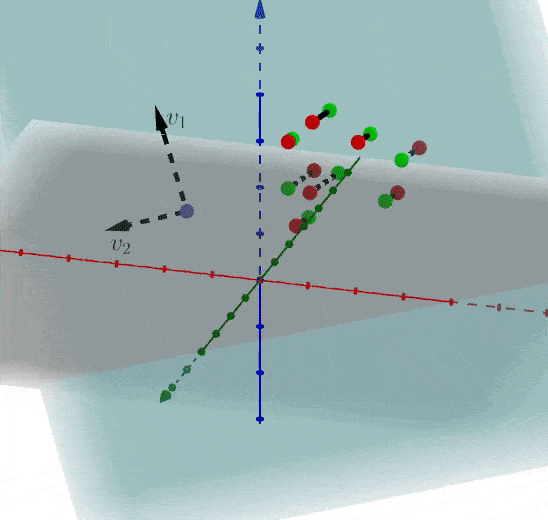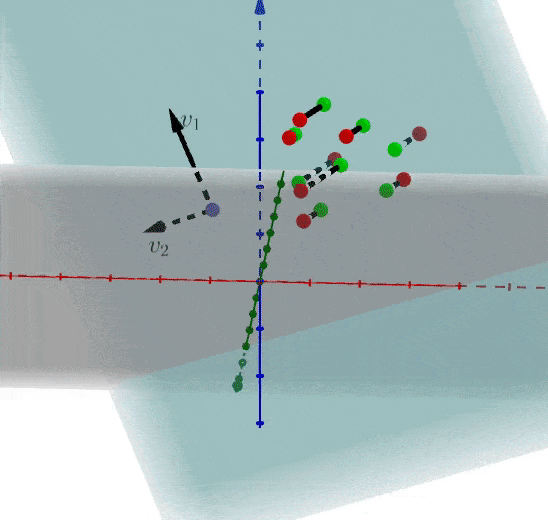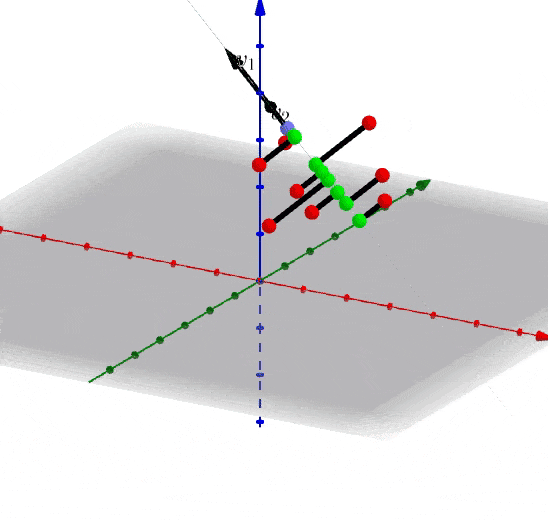
很容易知道如何生成多于二维的数据,之前是投影到直线上,现在是投影到一个平面上,下面是以3D为展示投影关系。
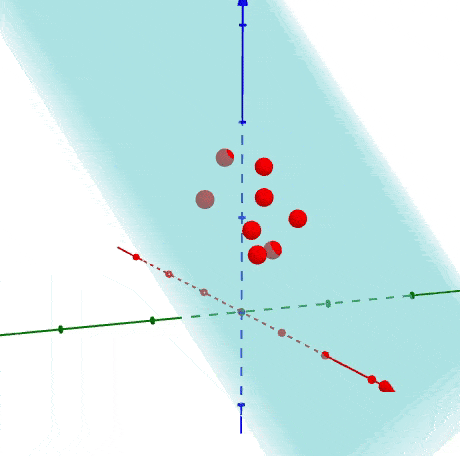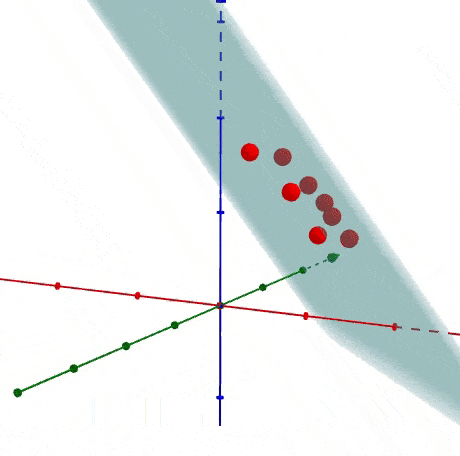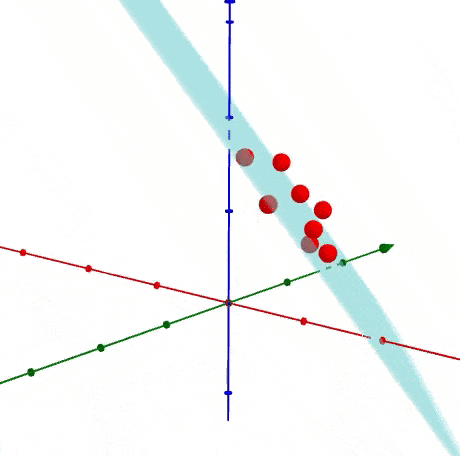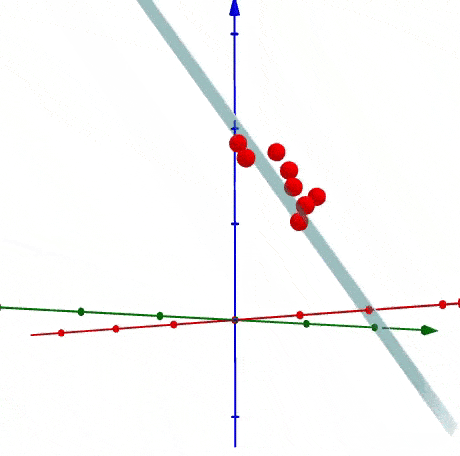
1.4 如何找到主成分线
具体不再此节中展示,后续SVD会进行详细展示
二. 概念介绍
2.1 內积(Dot、点积)
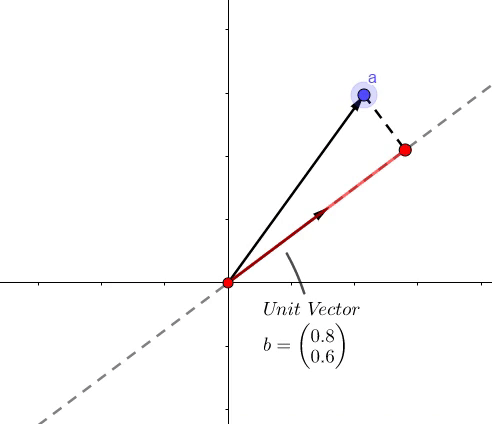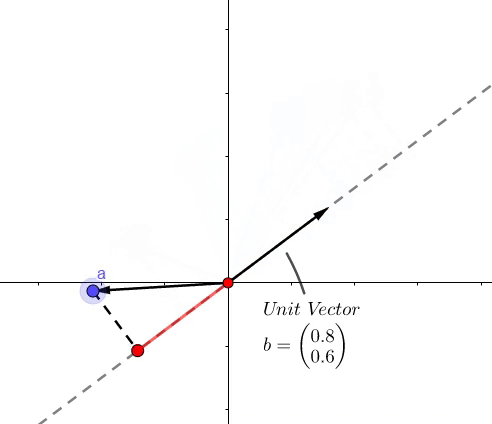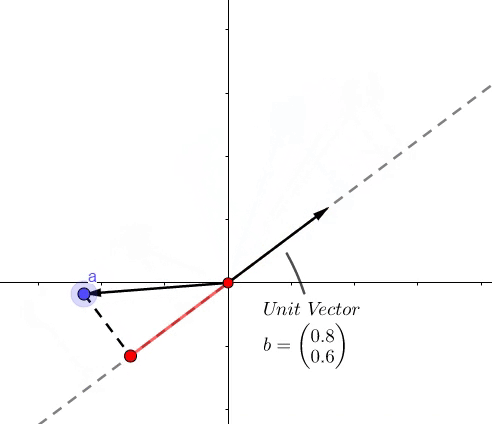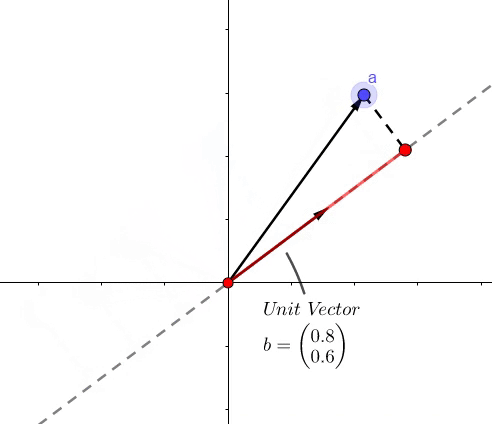
点积的结果是,虚线上红色的长度。
这么简单的事情,但是具有非常大的应用范围。我可以告诉你,以后我们做的所有事情,都可以用一系列点积去表示,别感受惊讶。点积可以看做很多方面:
- 像上面的图所示,可以表示一个向量 \(b\) 到向量 \(a\) 的投影长度
- 向量 \(a\) 和向量 \(b\) 的靠近程度 \(a \cdot b = |a||b|cos\theta\)
- 最短距离(上面式子)
- \(a\) 和 \(b\) 其中的一个分量
以上的点都差不多,都是通过一个公式可以展示出来。
举个例子,\(a=(1,2)\),\(b=(0.8,0.6)\) :
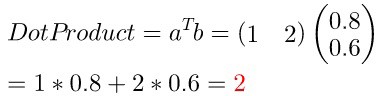
2.2 多维点积
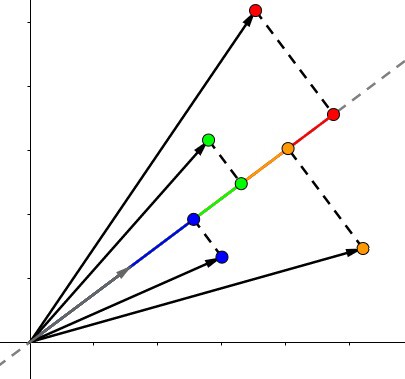
简要概述:多维矩阵点积,不做过多介绍。
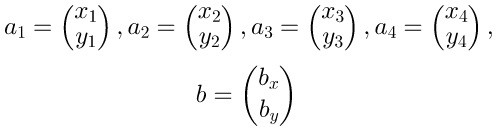
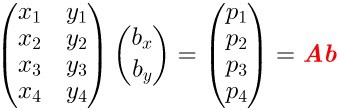
2.3 反向求解
矩阵的一些性质,不做过多介绍
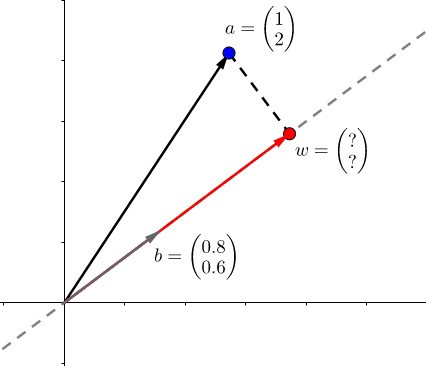
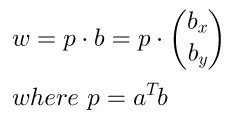
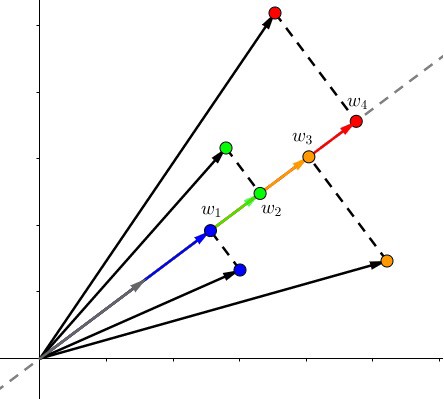

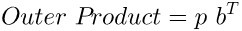
2.4 翻转矩阵

趣事:当逆陷入困境的时候,请问问你的猫。如果它像上面图像一样面对你,说明它想告诉你-----改变你的视角,你会发现很多有趣的事情。
我们以实际的数据进行描述,假设存在两个城市,有三天的数据,也就是 \(X_{3*2}\) 的矩阵,将这矩阵在二维平面进行作图。

上图并没有什么鼓舞人心的事,让我们换个视觉,像猫一样:

我们得到了不同于之前的一个矩阵,现在我们在三维空间进行绘图:
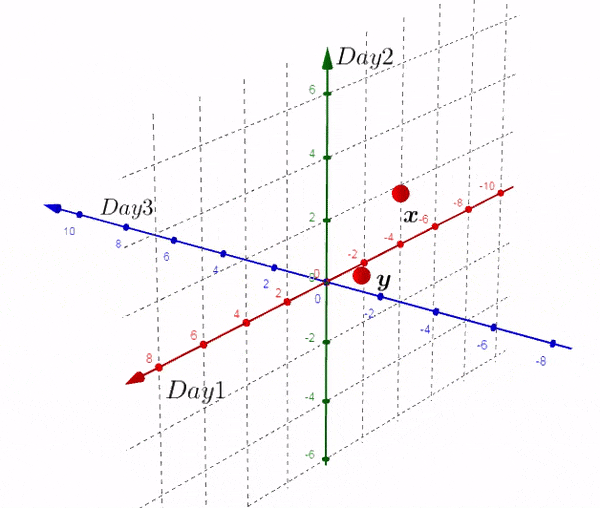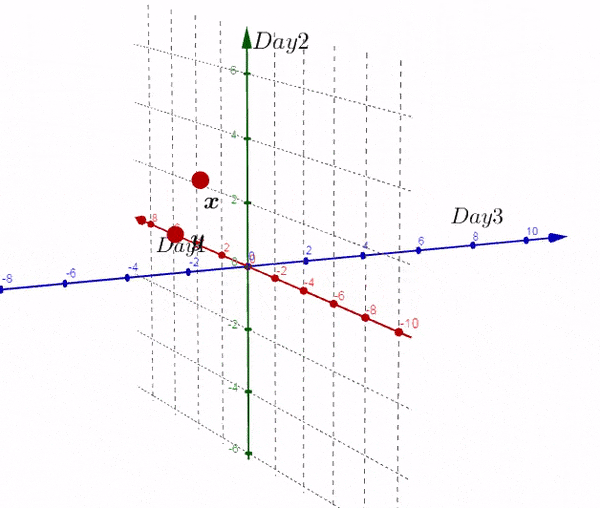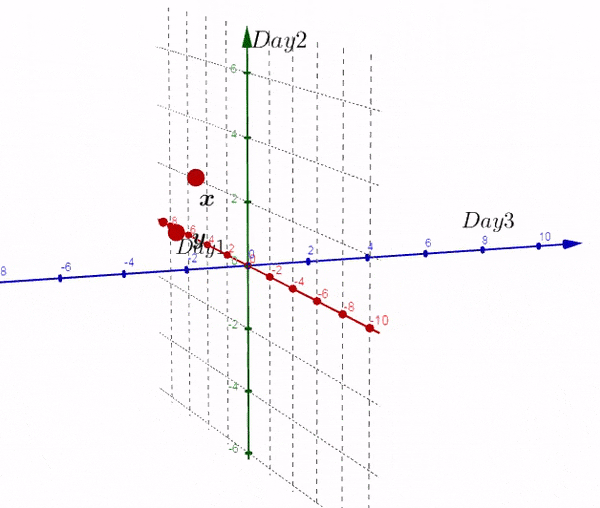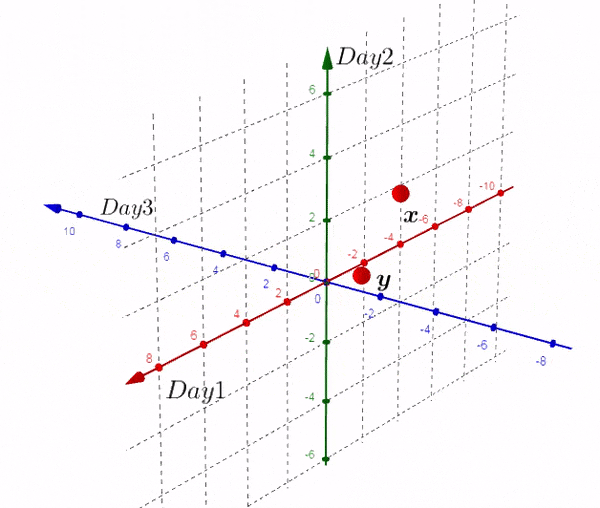
完全理解转换后的矩阵非常重要:
- 新的矩阵以Day为轴,而之前的数据则相反
- 新矩阵中每一行的数据是3D空间中的一个点
- 新矩阵第一行的数据是由每一天形成的。。。
- 如果我们有大于三天的数据,结果也是两个点。
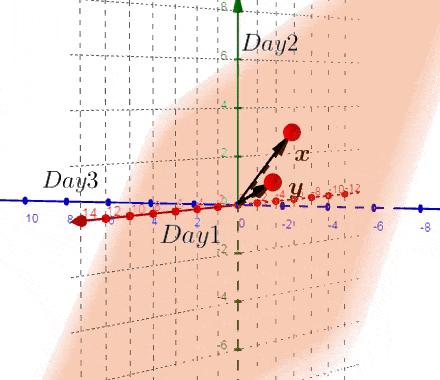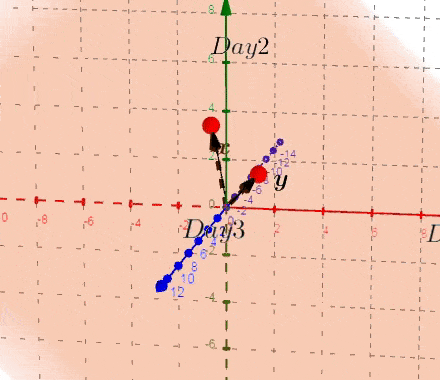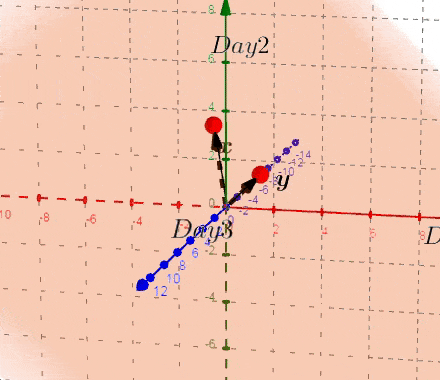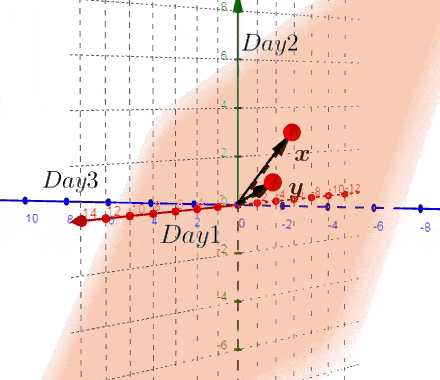
到目前为止,我们画出一个唯一的平面,如果我们画出这个平面和原始的散点图,称之为:双重图。
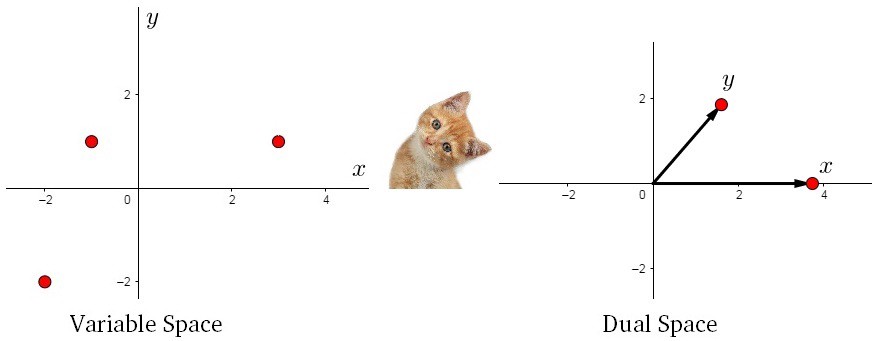
2.5 新空间
现在,我们可以在新的双平面中进行探索一些特性。为了更好地理解,我们先看两个空间的联系:

声明#一: 方差就是红色箭头(\(x\))和蓝色箭头(\(y\))的长度。可以从左图来看,\(x,y\) 是等比例变换的,不存在协方差,只有方差的存在。

声明#二:协方差就是红色箭头(\(x\))和蓝色箭头(\(y\))的夹角。可以从左图来看,\(y\) 轴方差不变,\(x\) 轴方差变大,协方差改变。
2.6 具体公式
方差:
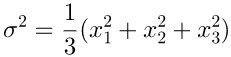
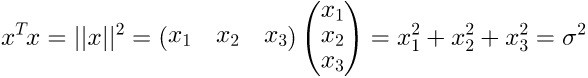
协方差:
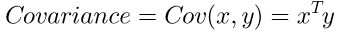
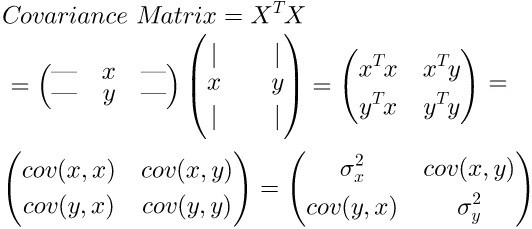
这部分原作者介绍很多,比较容易理解,这里不进行整篇翻译。。。
补充:
- 这里的数据都是经过中心化的,减去均值之后。
- 从方差到协方差,可以简单的想成数据到矩阵的变换
- 这部分主要介绍了方差(数据)和协方差(矩阵)的求解方法。但是我们还是无法找到主要的特征方向(PCA),假设\(A\)、\(B\)、\(C\)三个特征,\(\sigma_A > \sigma_B > \sigma_C\) ,我们无法直接将\(C\) 特征去除,因为加入\(A\) 和 \(B\)的相关性很大,得到的\([A,B]\)矩阵没没有意义的。
三. PCA操作
3.1 明确目的
在没有进行明确定义之前,你无法解决如何找到最大方差的方向。也就说明我们必须明确定义什么是方差?从之前的章节中,我们知道如何求解方差和协方差,但是无法求解主方向,如果得到主方向,那么就知道主方向上的投影,计算投影的协方差即可。
注释:
之前说的\(X\)轴方向的特征,指的是沿着\(X\)方向的特征。
下面这幅图在之前出现过,这里再强调一下!之前的轴是\(,x_2,x_2\),新的轴是\(,z_1,z_2\) ,注意我们都是在找到主方向之后,才去计算方差和协方差的,然后再去除某个方差小的特征。我们不是在任意数据上都直接计算方差,比如下附图,我们没有直接使用\(,x_1,x_2\)去计算他们的方差,这没有意义。

仔细的观察,我们注意到一点:假设我们找到了主方向,是不是数据在主方向上的投影就代表着数据本身?上图新轴中,\(z_1\) 轴的投影就是数据沿 \(z_1\) 方向的分布,也就是直接计算这个投影就是代表计算新数据的特征。请仔细体会!
前面我们知道投影长度的公式,假设有矩阵 \(A\),他的主方向是 \(v\),则投影长度为\(p\)
那么我们只需计算\(A\)矩阵在主方向上的投影\(p\)的方差即可,目的是寻找最大的方差:
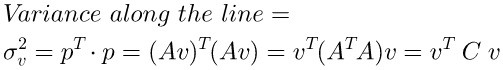
3.2 探索协方差
之前我们从猫那里学习到数据可以进行旋转,或许会发现又去的事情。对于矩阵的旋转,我们可以看一下特征值和特征向量。其公式来历不过多介绍
其中特征向量是单位矩阵和正交矩阵:
现在将问题简单化,假设 \(C\) 为二维的矩阵,利用上面的正交基\(,v_1,v_2\)


因为 \(u\) 为正交矩阵,所以\(k_1^2+k_2^2=1\) ,也就是说\(、k_1、k_2\)的取值为\([-1,1]\),如何使得 \(\sigma^2\) 最大化,这就比较容易了,当\(\sigma _1 > \sigma_2\) 那就使得\(,k_1=1,k_2=0\),反之亦然
其实这个时候结论已经出来了,原作者还是补充了一个例子:
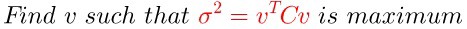
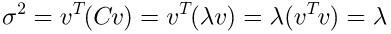
上面的例子不做说明了,直接看推导公式即可。
结论:矩阵在特征向量上的最大方差等于他的特征值
3.3 PCA引出
还记得第一章介绍的内容吗?想减少一个维度,我们直接对数据进行\(x_1\)轴上的投影即可。当前我们按照推导的公式进行操作,假设存在矩阵\(A\),协方差矩阵\(C\),特征向量\(、v_1、v_2\),我们可以获得在主方向上的投影为\(A\cdot v_1\)

维度提升到三维,特征向量为\(、、v_1、v_2、v_3\),\(C\) 的特征向量为\(E\)
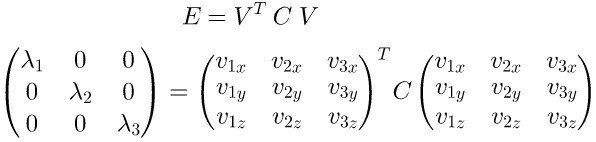
假设我们选择抛弃\(v_3\)轴的特征,也就等于矩阵\(A\)在\(、v_1、v_2\)上投影即可:
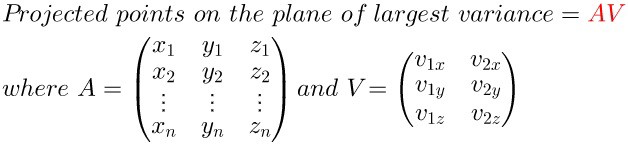
我们反过来看一下,当知道协方差矩阵\(C\)时,可以被分解为特征值和特征向量的点积

统计一下PCA的操作步骤:
- 所有数据减去均值(方便计算)
- 计算协方差:\(C=A^T\cdot A\)
- 分解\(C\)求解特征值和特征向量
- 选择较大的特征值(90%或95%)
- 投影到新的特征空间
四. SVD操作
4.1 SVD推导
回顾高中物理力学知识,力是矢量,假设\(F\)为二维平面的力,可以被分解为\(,x,y\)方向的分量:
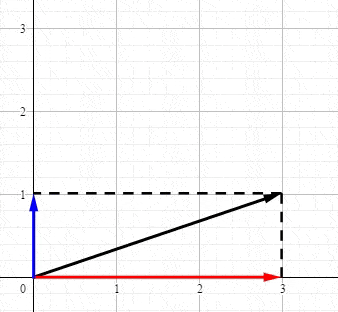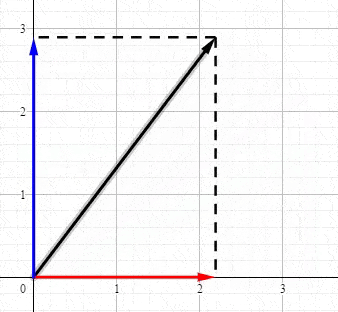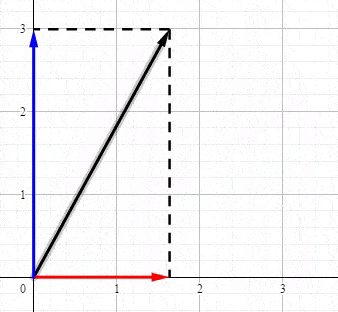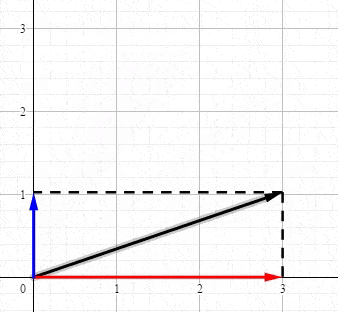
比较遗憾的事,几乎所有的教程都将SVD复杂化了,而其核心非常简单。因为数学就是将相同的概念赋予不同名字的艺术。我们仅仅是需要一个高大上的名字而已,其实SVD就是分解矩阵成正交空间。我们分解向量\(a\)得到三块的信息:
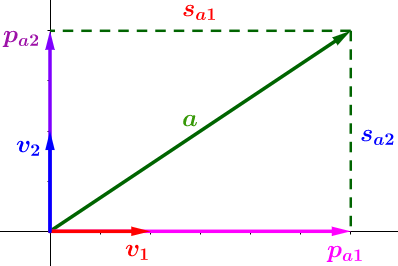
- 投影的方向,\(、v_2、v_2\) 正交
- 投影长度,\(S_{a1} > S_{a2}\),所以在\(v_1\)方向的信息更重要(丰富),仔细理解,这是SVD的核心
- 投影向量,\(、P_{a1}=a\cdot v_1、P_{a2}=a\cdot v_2\)
如何处理多个数据?这就是矩阵的优势了、、、
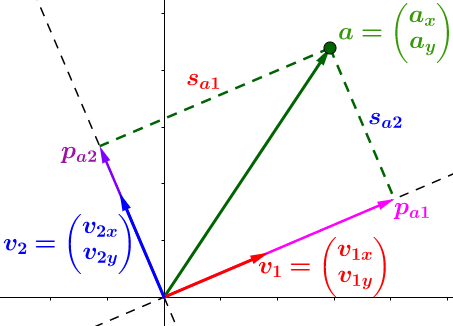
先从简单的二维平面说起,扩展到多个多维数据。下图,将向量\(a\)投影到\(、v_1、v_2\)平面,注意不是之前的\(、x、y\)轴!操作和之前一样,只是基改变了
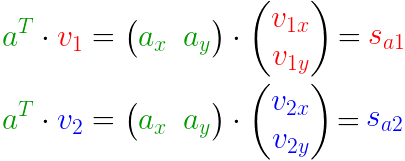
- \(A\):待求矩阵
- $ V$:投影方向(基)
- $S $:投影长度
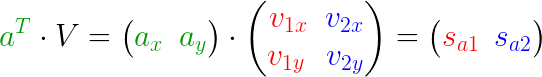
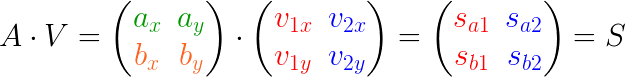
扩展到多个点的情况:
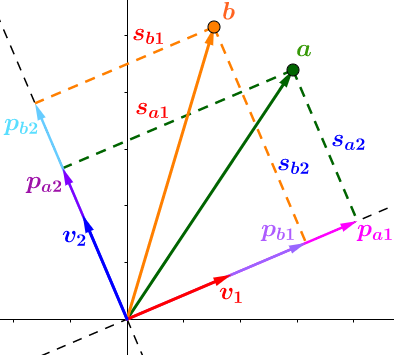
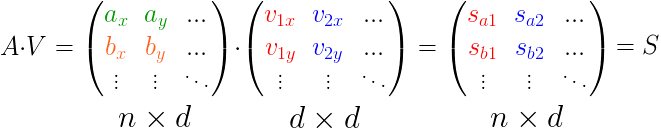
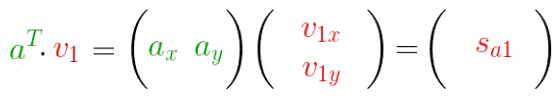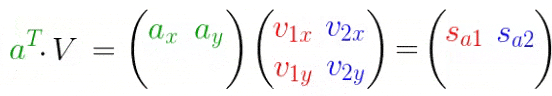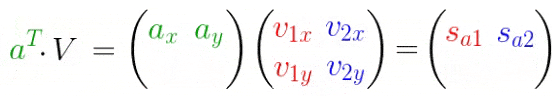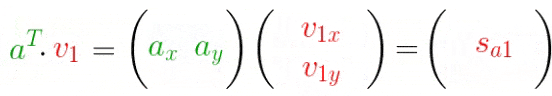
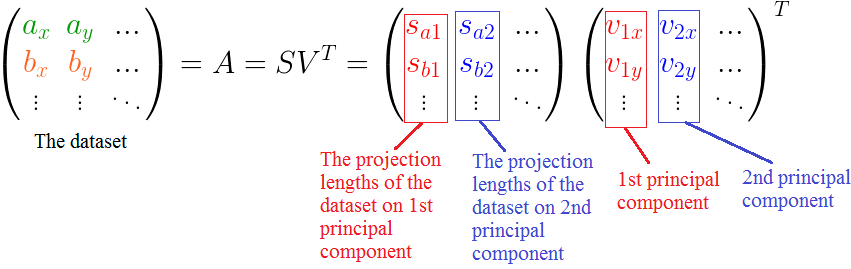
反转一下,变换成矩阵分解的式子:

我们先看看正常的SVD公式:
按照我们上述推导的结论,和SVD公式结合理解:
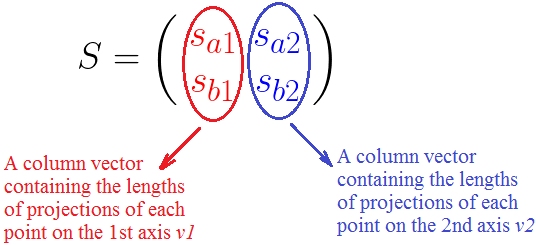
有了上面的推导,这里给出一个具体的例子:

之前我说过SVD的核心是投影的长度越大,这个轴上的数据越重要,那么我们就按照长度进行划分:
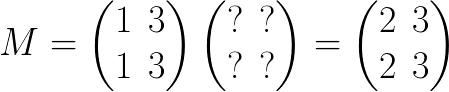

这里将平局长度进行了提取,更容易进行判断:
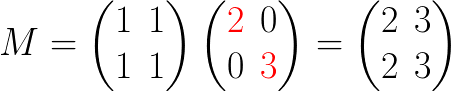
现在可以给出一个通用的公式:
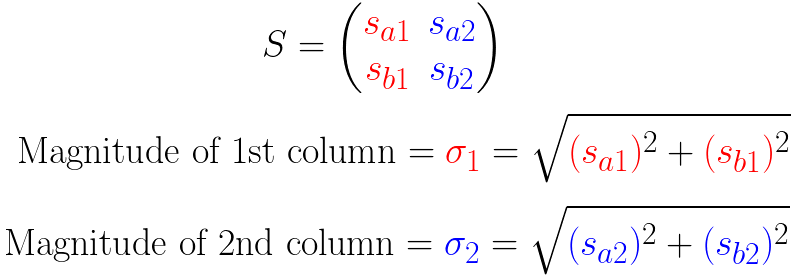
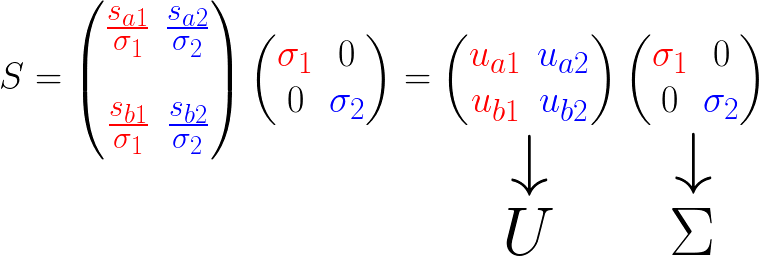
简单的说明:

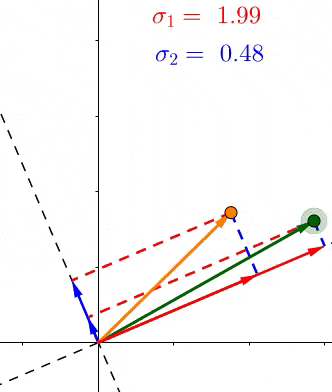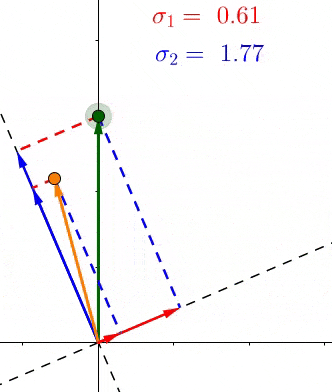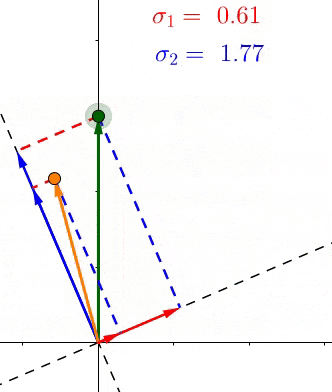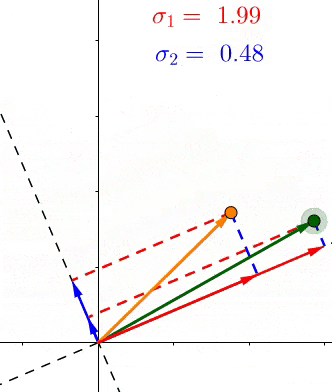
- \(、\sigma_1、\sigma_2\)是轴上投影的长度平方和的均方根(平均长度)
- \(if:\sigma_1>\sigma_2\) 说明大多数的点更靠近\(v_1\),也就等于特征\(v_1>v_2\),反之亦然。
4.2 PCA与SVD
之前我们介绍了PCA的操作,求取主成分方向,最大的方差就是我们求取的主要方向,然后进行投影就可得到目标矩阵。
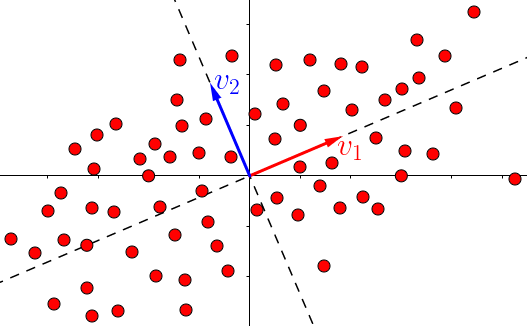
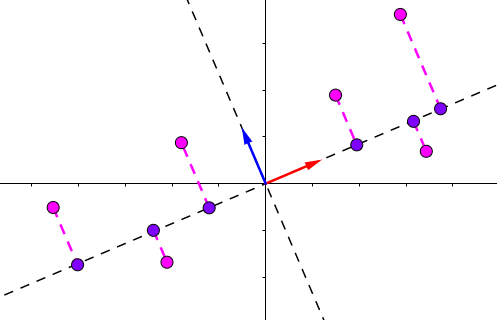
SVD和PCA不同,所有的点都进行了投影,而且在不同的特征上,下图中第二主成分也找到了,同理更多的维度也是这样排列。
如何取重要成分?按照公式即可,直接取出多余的特征,重新投影到新的特征空间,步骤和PCA类似。(里面的例子是只按照第一主成分进行投影,当然你可以按照其他主成分进行投影,或选择多个主成分)

PCA和SVD的个人理解
-------------------------------------------
个性签名:衣带渐宽终不悔,为伊消得人憔悴!
如果觉得这篇文章对你有小小的帮助的话,记得关注再下的公众号,同时在右下角点个“推荐”哦,博主在此感谢!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号