字符串专栏
前言
字符串这东西吧,感觉不是很好评价,学了n遍也依然学不会,反正是能学一点是一点吧感觉。
最近两天来机房其实都挺摆烂的感觉,因为作业都是有一半题我都写过的,所以开始猛猛写总结。
知识点
前缀函数
对于一个字符串 \(s\) 来讲,其前缀函数就是其最长的相等的真前缀和真后缀的长度。
举个例子,对于字符串aabaa来讲,其前缀函数值是 \(2\),因为它的最长相等真前缀和真后缀为aa,对于aaba和abaa来讲,他们两个实则并非是相等的串。
于是,很显然,我们发现了一个非常简单的 \(O(n^3)\) 的朴素求前缀函数的方法,只需要暴力枚举相等的前后缀长度应为多少,然后 \(O(n)\) 地检查一遍即可。
但是呢,显然,\(O(n^3)\) 的时间复杂度还是有点太过于强悍,所以考虑进行优化。
我们容易发现,对于一个字符串 \(s_{[1,i]}\),满足
证明:
显然对于前一个字符串有 \(s_1\sim s_{nxt_{i-1}}=s_{i-nxt_{i-1}}\sim s_{i-1}\),如果要是当前的相同前后缀最长,显然应该有 \(s_i=s_{nxt_{i-1}}\)。此时该字符串的相同前后缀长度为 \(nxt_i=nxt_{i-1}+1\)。
如果不满足以上条件,则依据定义,有
但是以上结论之间产生矛盾,顾该假设不成立。
发现了这个性质以后,算法很容易优化成了 \(O(n^2)\) 的。
但是显然,我们还需要进一步优化。上述优化产生于 \(s_i=s_{nxt_{i-1}+1}\),而目前时间复杂度的瓶颈产生与当二者之间不满足上述条件时,重新进行匹配所需代价,所以我们考虑不满足的情况下如何优化。
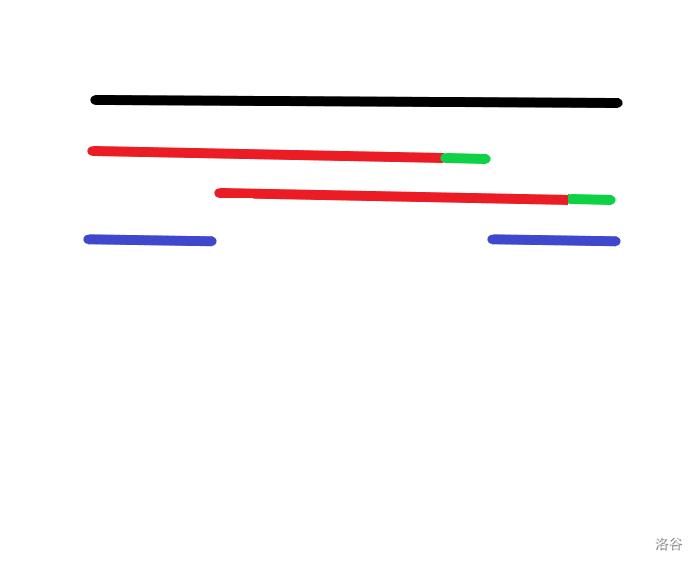
在上图中,黑色的线表示整个字符串,红色的先表示之前匹配上的字符串,绿色的线表示当前未匹配上的字符,蓝色表示最终该字符串的最长相同前后缀。
仔细观察之后可以发现,每条蓝色的线除去最后一个字符,其他的字符同时是红色线的一组相同前后缀,为使最终的匹配最大化,显然应当是其最大相同前后缀才可以是串 \(+1\) 后的匹配长度最大。
因此,我们的最终版算法应运而生,每次不匹配时向前寻找前一组匹配的最长相同前后缀进行匹配,如果能匹配上,就停止,否则,继续向前匹配。
给个代码,其实是从KMP代码上粘贴下来的。
for(int i=2,j=0;i<=m;i++){
while(j&&s2[j+1]!=s2[i]) j=ne[j];
if(s2[i]==s2[j+1]) j++;
ne[i]=j;
}
KMP
讲完了前置知识前缀函数,KMP也就十分简单了。
KMP用来求对于一个长串中某个短串出现了多少次非常简单。
对于两个给定的只有字母的字符串 \(s1\) 和 \(s2\),我们要求 \(s1\) 在 \(s2\) 中出现了多少次。
显然,将 \(s2\) 添加到 \(s1\) 的后面,中间用 \(#\) 隔开,做该串的前缀函数,最后对其从前到后扫一遍,看有多少个串的前缀函数值等于 \(s2\) 的长度即可。
至于为什么没有串的前缀函数值会超过 \(s2\),又为什么不会记重,是因为 \(#\) 的功劳。在该字符串中,只有字母,没有其他符号,所以自然不会出现一个与 \(#\) 匹配的字符,自然也就不会有串的值超过了。
感觉自己讲的非常之干涩,明明学的时候快被难死了,非常之无语,深刻认识到了学好语文的重要性。
酸解版本
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+100;
char s1[N],s2[N];
int n,m;
int ne[N];
int read(){
int t=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9') {
if(ch=='-') f=-f;
ch=getchar();
}
while(ch>='0'&&ch<='9') {
t=t*10+ch-'0';
ch=getchar();
}
return t*f;
}
int main(){
scanf("%s",s1+1);
n=strlen(s1+1);
scanf("%s",s2+1);
m=strlen(s2+1);
ne[1]=ne[0]=0;
for(int i=2,j=0;i<=m;i++){
while(j&&s2[j+1]!=s2[i]) j=ne[j];
if(s2[i]==s2[j+1]) j++;
ne[i]=j;
}
int ans=0;
for(int i=1,j=0;i<=n;i++){
while(j&&s1[i]!=s2[j+1]) j=ne[j];
if(s1[i]==s2[j+1]) j++;
if(j==m) {
cout<<(i-m+1)<<endl;
j=ne[j];
}
}
for(int j=1;j<=m;j++){
cout<<ne[j]<<" ";
}
cout<<endl;
return 0;
}
自己悟出来的
#include<bits/stdc++.h>
using namespace std;
int n;
const int N=2e6+100;
int ne[N];
char s[N],s1[N];
int read(){int x;cin>>x;return x;}
int main() {
scanf("%s",s1+1);
scanf("%s",s+1);
int n=strlen(s+1);
int m=strlen(s1+1);
s[n+1]='#';
for(int i=n+2,j=1;j<=m;j++,i++) {
s[i]=s1[j];
}
// return 0;
for(int i=2,j=0;i<=n+m+1;i++) {
while(j&&(s[j+1]!=s[i])) {
j=ne[j];
// cerr<<j<<" "<<endl;
}
if(s[j+1]==s[i]) j++;
ne[i]=j;
}
// return 0;
int ans=0;
for(int i=1;i<=n+m+1;i++) {
if(ne[i]==n) cout<<i-n*2<<endl;
}
for(int i=1;i<=n;i++) {
cout<<ne[i]<<" ";
}
cout<<endl;
return 0;
}
AC自动机
其实就是把 KMP 在字符串上干的事情挪到了 tri 树上干,所以最困难的其实还是怎么快速地处理出来当当前字符串不匹配时要怎么跳到最长相同前缀那里去。
这次我们使用一个 fail 数组,令 \(fail_i\) 表示当前从 \(root\) 到节点 \(fail_i\) 是 \(root\) 到节点 \(i\) 的一个后缀,且是满足条件的最长后缀。每次更新时,只需要暴力地往 \(fail_i\) 跳就好。
那么,如何维护这个 fail 数组呢,答案就是————画图。
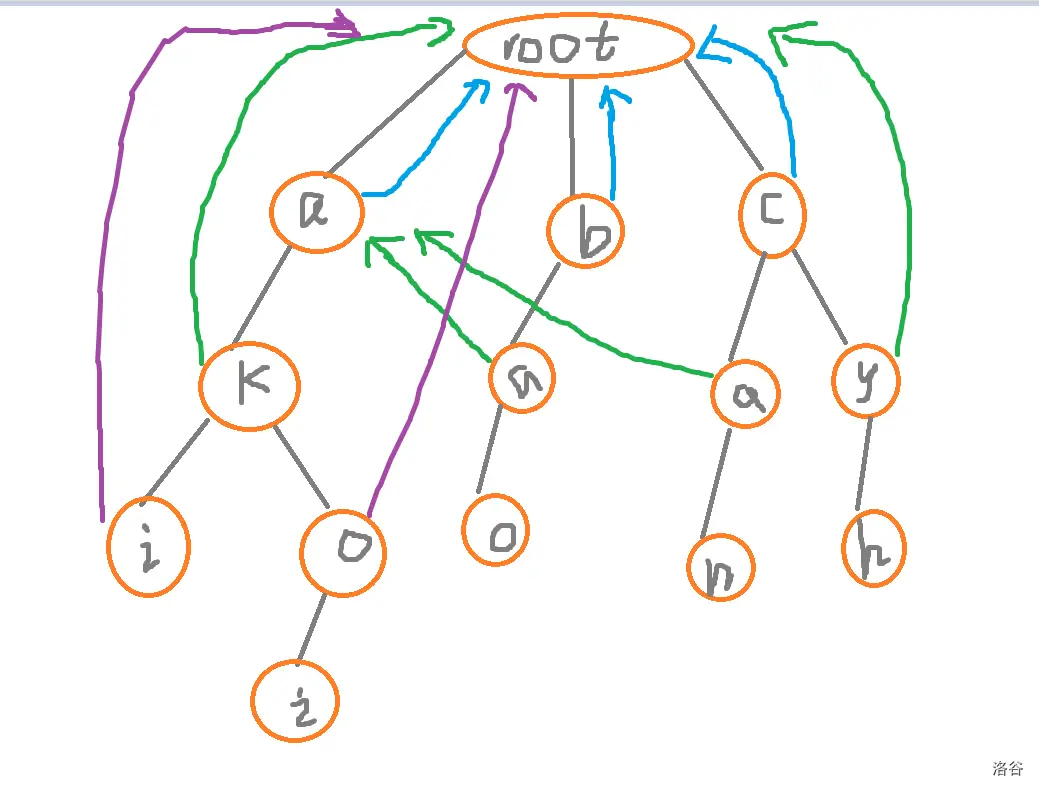
我们根据从 luogu 上偷的图来看,显然时按照不同颜色表示不同层数,一层一层向上推出来的,那这是个巧合吗,显然不是,和 KMP 一样的证明方法,我们容易发现,每个点都是从其父亲节点的 \(fail\) 的另一个节点递推下来的,所以我们认为,bfs 然后写一写就好了,如果依然没看懂的话,建议参考这篇题解。
为了防止再次出现上午听懂了但是不会实现的事情,我们决定,给出我宝贵的代码。
容易发现,3个月后再次打开这个,发现自己已经看不懂,遂前来给出一点补充。
什么叫做每个点都是从其父节点的 \(fail\) 的另一个节点推下来的呢,显然就是,我们找到这个点的 \(fail\),然后看这个 \(fail\) 有没有和它一样的儿子。
#include<bits/stdc++.h>
using namespace std;
int n,num=0;
const int N=2e5+100;
string t[N];
int tree[N][26];
int cnt[N],fail[N],ans[N],ru[N],flag[N],son[N],vis[N];
bool lef[N];
int read(){int x;cin>>x;return x;}
void build(string s,int id) {
int pos=0;
for(int i=0;i<s.size();++i) {
if(tree[pos][s[i]-'a']) pos=tree[pos][s[i]-'a'];
else {
tree[pos][s[i]-'a']=++num;
pos=num;
}
}
flag[id]=pos;
}
void bfs() {
queue<int>q;
for(int i=0;i<26;++i) {
if(tree[0][i]) {
q.push(tree[0][i]);
fail[tree[0][i]]=0;
ru[0]++;
}
}
while(q.size()) {
int x=q.front();q.pop();
for(int i=0;i<=25;++i) {
if(tree[x][i]) {
// if(tree[x][i]==8) cerr<<"lk3l23 "<<tree[fail[x]][i]<<" "<<x<<" "<<fail[x]<<endl;
fail[tree[x][i]]=tree[fail[x]][i];
ru[tree[fail[x]][i]]++;
// cerr<<"dslfk "<<tree[fail[x]][i]<<" "<<tree[x][i]<<endl;
q.push(tree[x][i]);
}
else tree[x][i]=tree[fail[x]][i];
}
}
}
void find(string s) {
int pos=0,sum=0;
for(int i=0;i<s.size();++i) {
pos=tree[pos][s[i]-'a'];
++ans[pos];
// cerr<<pos+1<<endl;
}
}
void topu() {
queue<int>q;
for(int i=0;i<=num;i++) {
if(ru[i]==0) q.push(i);
}
while(q.size()) {
int x=q.front();q.pop();
// cerr<<"sdklfkj "<<x+1<<endl;
ans[fail[x]]+=ans[x];
ru[fail[x]]--;
if(ru[fail[x]]==0) q.push(fail[x]);
}
}
void init() {
memset(fail,0,sizeof(fail));
memset(ru,0,sizeof(ru));
memset(ans,0,sizeof(ans));
memset(tree,0,sizeof(tree));
num=0;
}
void work() {
init();
for(int i=1;i<=n;++i) {
cin>>t[i];
build(t[i],i);
}
bfs();
string s;
cin>>s;
find(s);
topu();
int maxx=0;
for(int i=1;i<=n;++i) {
maxx=max(maxx,ans[flag[i]]);
}
cout<<maxx<<"\n";
for(int i=1;i<=n;i++) {
if(ans[flag[i]]==maxx) cout<<t[i]<<"\n";
}
return;
}
int main() {
while(1) {
n=read();
if(n==0) return 0;
work();
}
}
manacher
一直没有去学,断断续续拖了有快一年了吧,每次都是看懂题解了,不想写代码,到最后也没有搞,但是前两天模拟赛考了,这下不得不去学了。
简单来说,这就是一个能够在线性时间复杂度内求回文串的东西。
详细讲讲这玩意的工作原理。
首先,因为回文串有两种情况,长度可以为奇数或者偶数,所以我们考虑在每两个相邻的字符里面插上什么特殊字符,这样就可以忽略掉奇偶需要分类讨论的问题了。
然后,你考虑平常你找回文串,最暴力的显然就是直接 \(O(n^2)\) 地去找,这样显然不优对吧,所以我们对着这个暴力进行优化,就是如果当前的位置已经是位于某一个回文串里面的了,那么从这个点到回文串最右边这一段是不是在以当前点为中心的回文串中是可以直接通过前面一半推得,所以你就只需要从你没有到过的那个位置开始跑,这样,你每次就不需要把整个序列都遍历一遍,因此,时间复杂度就是线性的没错了。
#include<bits/stdc++.h>
using namespace std;
int n,tot=0;
const int N=3e7+100;
char s[N],t[N];
int man[N],ans=0;
int read() {int x;cin>>x;return x;}
void manacher() {
for(int r=0,mid=0,i=1;i<=tot;i++) {
man[i]=(i<=r?min(man[mid*2-i],r-i+1):1);
while(t[i+man[i]]==t[i-man[i]]) man[i]++;
if(i+man[i]>r) {
r=i+man[i]-1;
mid=i;
}
if(man[i]>ans) ans=man[i];
}
}
signed main() {
scanf("%s",s+1);
n=strlen(s+1);
tot=1;
t[0]='(';
t[1]='*';
for(int i=1;i<=n;i++) {
t[++tot]=s[i];
t[++tot]='*';
}
manacher();
cout<<ans-1<<endl;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号