P11370 [Ynoi2024] 堕天作战/虚空处刑

不是我想写的，是lxl老师布置的题单里有。
仿照P3316的思路，我们将多边形的每一条边按横坐标分拆到\(O(\log n)\)个线段树节点上。
不过现在我们就需要讨论两种情况，一种是查询所在结点在修改（指初始的多边形的边）下方，

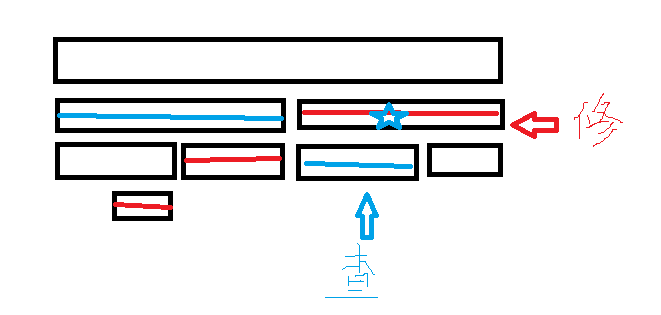
我们在所有查询结点在线段树上所有的祖先结点进行操作。
这样修改形成若干贯穿区间的直线,查询形成线段。

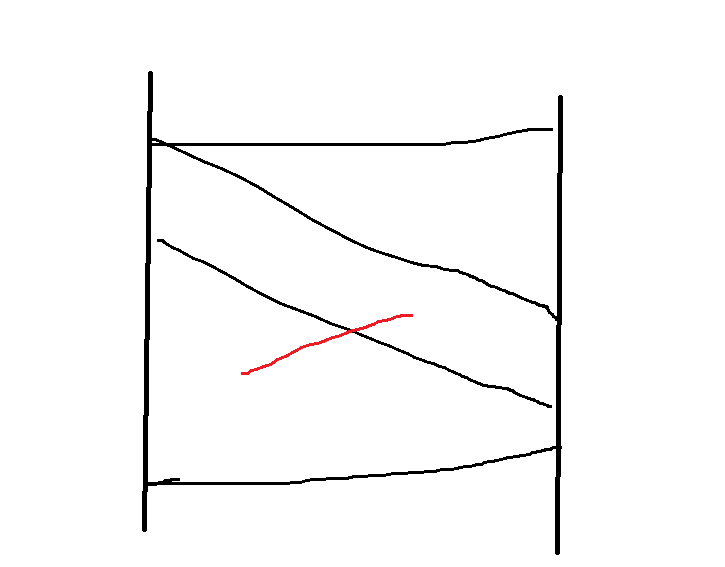
根据修改直线形成一个多边形，我们可以得知这些直线是不交的（至多交于端点）。
查询的时候便可以直接二分得到线段两个端点的rank，比较是否相等就好了。（判掉端点与直线相交）

另一种则是在下方。

这样的话多边形的边形成若干“牙齿”与”耳朵“：

(很像吧)
对于那些牙齿（也就是与区间左右端点相交的连通块），一条线段至多显然只会与它的前驱后继相交。

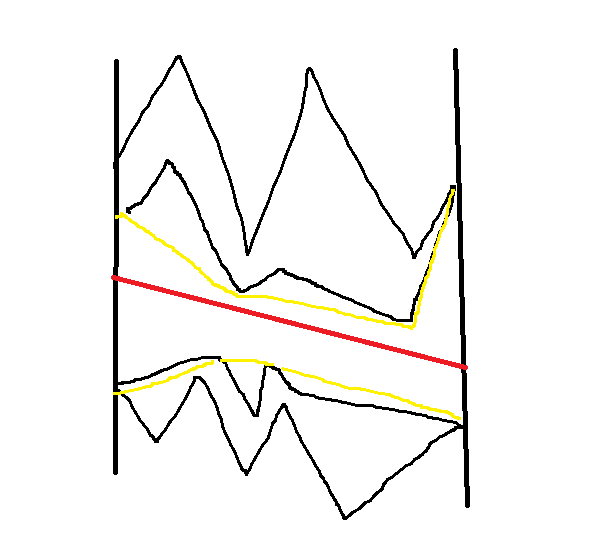
所以我们对每个牙齿求一个凸包，查询的线段（实质上现在是直线）在凸包上二分就好了。

重点是耳朵。
首先特判这种情况：

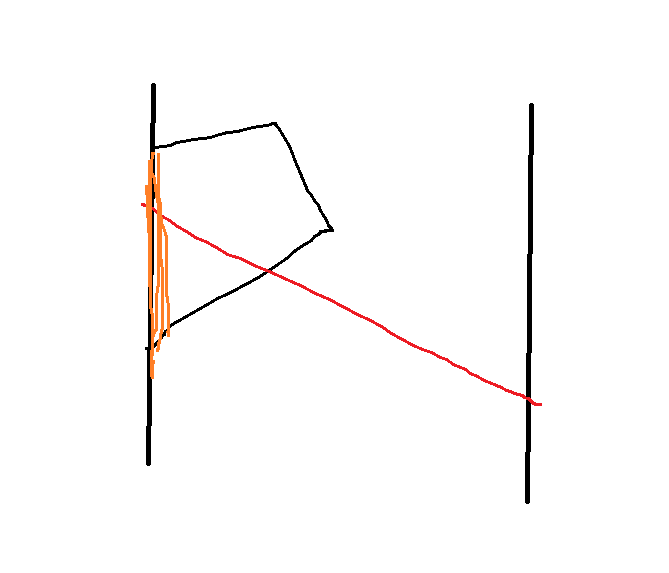
这个东西按耳朵与左半区间（右耳朵同理）的交排序之后二分就好了。

然后有一个误区是直线也至多与前驱后继的耳朵相交，但这是不对的。

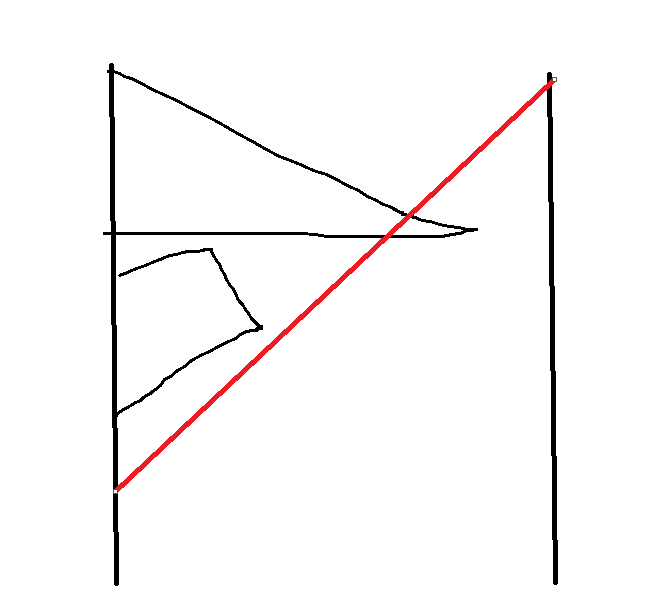
按左上作为例子，我们需要加入所有直线左上方的耳朵，并将它们的端点求个凸包就好了。这个过程可以离线之后扫描线解决。
合并凸包的时候比较麻烦，但其实我们只用维护凸壳，这个过程用双指针做，细细讨论就好了。
需要对四个方向分别做一遍。

最后有一个小问题，就是查询与修改都垂直于\(x\)轴，这个特殊处理一下，做一个区间加区间查，不是大问题。

没错这道题就是这样，思维难度不算高，但是代码确实难（也许想清楚了可以很快写完？）。

给几个样例：

3 10
7 1
4 4
5 7
1 6 4 1
5 5 8 6
9 10 1 1
2 6 4 2
4 9 9 3
6 8 10 7
2 5 4 6
6 3 6 9
6 3 10 1
5 2 2 2

NO
YES
YES
NO
NO
NO
NO
YES
YES
NO

10 1
6 13
7 11
11 12
16 8
9 3
4 4
2 4
11 6
3 15
16 20
12 8 1 9

YES

还给几组全是YES的样例（这些大的样例主要针对耳朵）：

task1:
15 1
58 49
25 82
45 99
32 78
61 51
52 60
45 71
62 80
77 20
73 94
98 46
93 4
15 14
64 52
7 13
52 76 3 100

task2:
15 1
7 24
13 2
45 34
34 14
197 42
77 33
163 87
69 28
64 38
179 142
119 72
186 142
108 154
39 139
24 70
197 129 95 41

task3:
13 1
63 152
165 199
41 176
4 84
29 13
76 96
58 107
93 115
53 157
123 92
168 138
185 93
170 165
38 128 73 97

task4:
10 1
33 11
41 33
24 31
13 35
36 50
46 46
39 41
50 13
23 5
21 28
50 27 40 50

task5:
12 1
15 31
30 39
4 46
3 18
40 7
45 26
29 18
9 19
38 26
29 37
14 26
9 24
50 32 17 43

task6:
15 1
39 28
20 9
73 15
75 16
96 54
73 34
35 32
81 70
65 71
65 73
16 91
12 92
63 68
40 51
20 13
55 71 12 12

task7:
13 1
31 12
49 24
28 39
42 28
6 43
6 31
11 29
3 29
1 13
5 4
36 8
12 13
2 19
8 46 3 31

task8:
10 1
14 47
30 1
49 6
30 7
30 11
38 14
42 33
45 30
41 50
7 47
28 7 39 27

剩下的自己拍。