Atcoder Regular Contest 191 (Div.2)

这个C是怎么回事？
更不更E？大概要稍等一会儿。
A
贪心做就完了，没什么可说的。
B
注意到若\(X \oplus N=X\bmod N\)，则\(N\le X<2N\)（\(X\)的最高位不能高于\(N\)的最高位）
所以\(X-N=X \oplus N\)
这样的话，当\(N\)的某一位是\(0\)时，\(X\)为\(0\)或\(1\)，否则\(X\)必须为\(1\)。
根据这个性质很容易求得第\(k\)小的\(X\)。
C
我唐了，打表为什么不打小一点呀。
你说得对，这是给定阶求底数和模数，但是为什么有人往这方面想一个小时呢？
官方给出的构造是\((N+1,N^2)\)，dengrk也是这样。
这个确实能证明，而且很容易证。
若\((N+1)^g\equiv 1\pmod{N^2}\)，则\(\sum_{k=1}^{g}\binom{g}{k}N^k\equiv 0\pmod{N^2}\)
那么\(gN\equiv 0\pmod{N^2}\)
\(g\equiv 0\pmod{N}\)
则\((N+1)\)模\(N^2\)的阶为\(N\)
D
分讨题，出这种东西有意思吗？
分以下几种情况讨论。
记\(s,t\)的最短路径长为\(X\)，令其为\(P\)

1. \(s,t\)之间存在至少2条长为\(X\)的路径。
   显然答案为\(2X\)，这是最优情况。
2. \(s,t\)之间存在长为\(X+1\)的路径。
   答案为\(X+1\)。除情况\(1\)外，不存在更优解法。
3. \(s,t\)的最短路径（不包括\(s,t\)）上有度数\(>2\)的点。
   
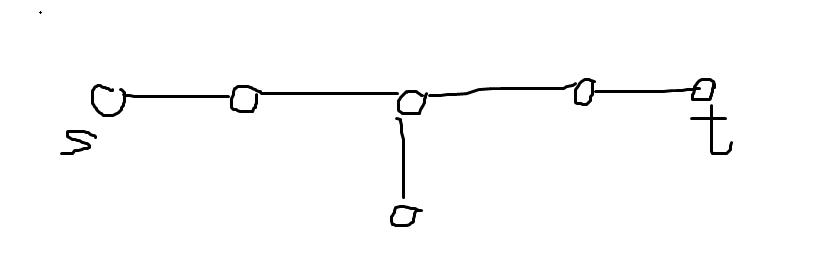
   形如上图，显然答案为\(2X+2\)

剩下的两种情况若存在则取min
4. \(s,t\)之间存在长度为\(Y\)的最短路径，且与\(P\)不交（除\(s,t\)）。
答案为\(X+Y\)，若有交就转为了情况\(3\)，那样显然不劣。
5. \(s,t\)可达最近的度数不为\(2\)的点。（保证\(s\)不经过\(t\)，\(t\)不经过\(s\)）
若\(s\)可达\(u\)，\(t\)可达\(v\)(\(s,t\)可以等于\(u,v\))
（不存在\(u,v\)则不计入答案）
若\(u,v\)度数都为\(1\)则形如这样：

显然在这种情况下无解。
否则当\(u\)度数大于\(3\)或\(v\)大于\(3\)，记\(z=\min(dis(s,u),dis(t,v))\)，若\(u,v\)度数为\(1\)则不计入。

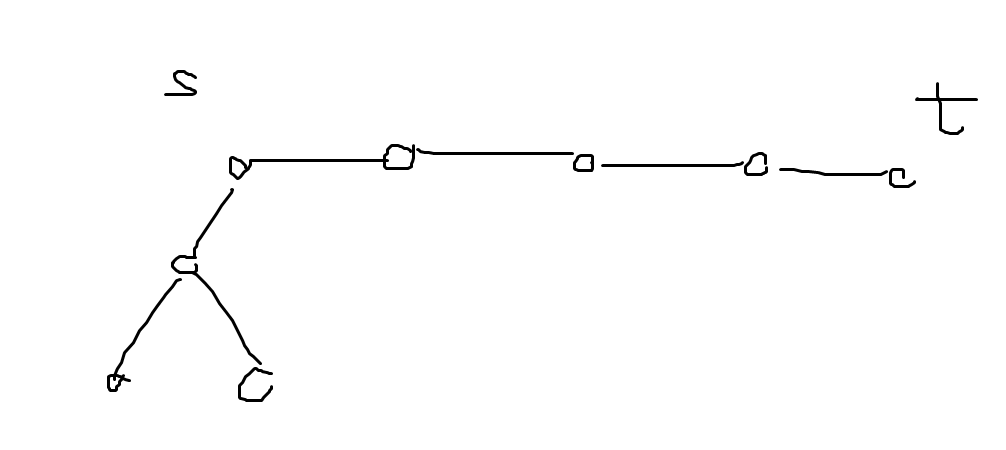
稍微手模一下就可知答案为\(2X+4Z+4\)

那么这道题就做完了，感觉不写拍子在赛时很难分讨完。
放个代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5,INF=1e9;
using ll=long long;
int n,m,s,t,d[N];
int head[N],to[N<<1],nxt[N<<1],tot;
int ans=INF;
int pre[N];
inline void add(int u,int v){nxt[++tot]=head[u],to[tot]=v,head[u]=tot;}
vector<int> gtm(int st){
	vector<int>dis;dis.resize(n+2);
	for(int i=1;i<=n;i++)dis[i]=INF;
	dis[st]=0;
	queue<int>q;q.push(st);
	while(!q.empty()){
		int u=q.front();q.pop();
		for(int i=head[u];i;i=nxt[i]){
			int v=to[i];
			if(dis[v]==INF){
				dis[v]=dis[u]+1;
				if(st==s)pre[v]=i;
				q.push(v);
			}
		}
	}
	return dis;
}
bool vis[N];
inline int find(int st,int ed){
	for(int i=1;i<=n;i++)vis[i]=0;
	queue<int>q;q.push(st);
	while(!q.empty()){
		int u=q.front();q.pop();
		if(vis[u])continue;
		vis[u]=1;
		if(u==ed)continue;
		if(d[u]^2)return u;
		for(int i=head[u];i;i=nxt[i]){
			int v=to[i];
			q.push(v);
		}
	}
	return 0;
}
struct node{
	int u,v;
}e[N];
bool vi[N];
int main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	cin>>n>>m>>s>>t;
	tot=1;
	int u,v;
	for(int i=1;i<=m;i++){
		cin>>u>>v;e[i]={u,v};
		add(u,v),add(v,u);
		d[u]++,d[v]++;
	}
	vector<int> ps=gtm(s),pt=gtm(t);
	int cur=0;
	for(int i=1;i<=n;i++){
		if(ps[i]+pt[i]==ps[t])cur++;
	}
	if(cur!=ps[t]+1){
		cout<<ps[t]*2<<"\n";
		return 0;
	}
	cur=0;
	for(int i=1;i<=n;i++){
		if(ps[i]+pt[i]==ps[t]+1){
			cur=1;break;
		}
	}
	if(cur){
		cout<<ps[t]*2+1<<"\n";
		return 0;
	}
	d[0]=1;
	cur=t;
	while(cur^s){
		if(cur^t){
			if(d[cur]>2){
				cout<<ps[t]*2+2<<"\n";
				return 0;
			}
		}
		vi[pre[cur]>>1]=1;
		cur=to[pre[cur]^1];
	}
	int ust=find(s,t),ued=find(t,s);
	int z=INF;
	if(d[ust]>2)z=min(z,ps[ust]);
	if(d[ued]>2)z=min(z,pt[ued]);
	if(z^INF)ans=min(ans,2*ps[t]+4*z+4);
	tot=0;
	for(int i=1;i<=n;i++)head[i]=0;
	for(int i=1;i<=m;i++){
		u=e[i].u,v=e[i].v;
		if(vi[i])continue;
		add(u,v),add(v,u);
	}
	ps=gtm(s);ans=min(ans,ps[t]+pt[s]);
	cout<<((ans==INF)?-1:ans);
	return 0;
}