求最大公约数的伪代码-20211318
作业要求
- 上网查找什么是求两个数的最大公约数的欧几里得算法(辗转相除法),提交算法说明和网上链接。
- 参考教材,用伪代码(英语或汉语)实现欧几里得算法(辗转相除法),提交伪代码。
- 选择几组数据,手动走一下伪代码,测试你写的伪代码是否正确,提交测试过程截图。
欧几里得算法
算法说明
以除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公约数
示例:
1997 / 615 = 3 (余 152)
615 / 152 = 4(余7)
152 / 7 = 21(余5)
7 / 5 = 1 (余2)
5 / 2 = 2 (余1)
2 / 1 = 2 (余0)
至此,最大公约数为1
证明
a可以表示成a = kb + r(a,b,k,r皆为正整数,且r
假设d是a,b的一个公约数,记作d|a,d|b,即a和b都可以被d整除。
而r = a - kb,两边同时除以d,r/d=a/d-kb/d,由等式右边可知m=r/d为整数,因此d|r
因此d也是b,a mod b的公约数。
因(a,b)和(b,a mod b)的公约数相等,则其最大公约数也相等,得证。
参考链接百度百科
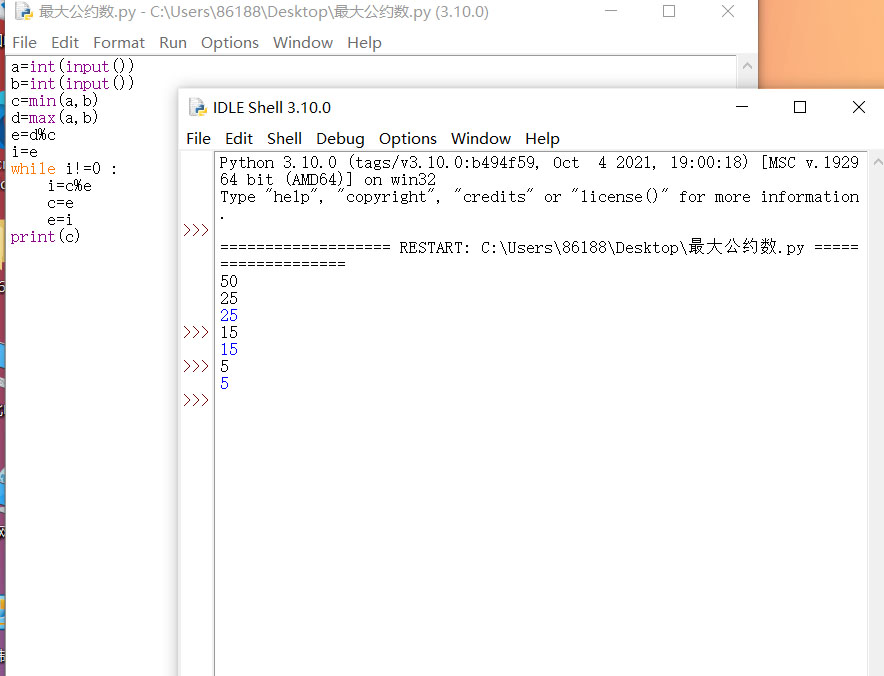
伪代码

伪代码的实现与测试



 浙公网安备 33010602011771号
浙公网安备 33010602011771号