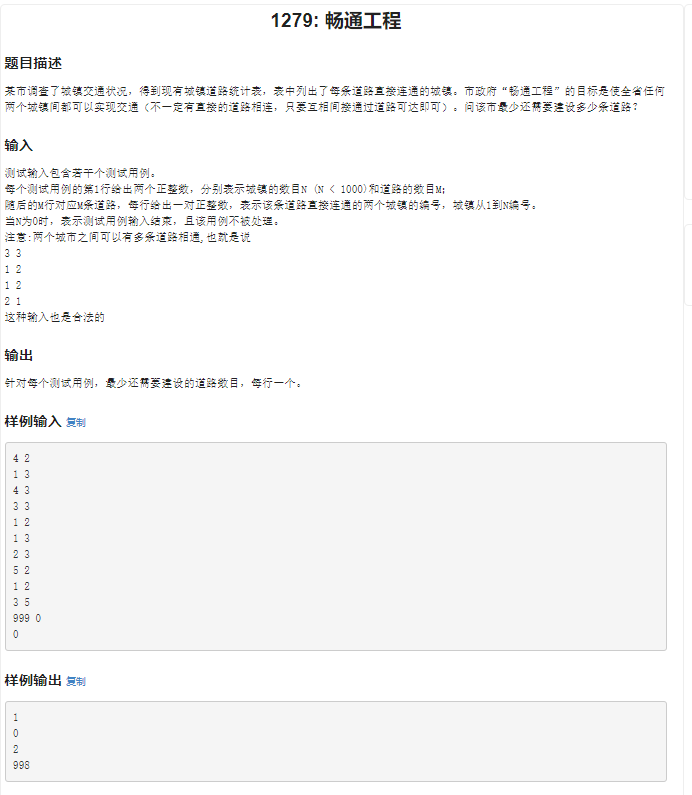
畅通工程

 

 这道题目又要用到新的算法：并查集

 

其实就是一个向上的递归过程，但我们只关心x点的祖先是谁，这里就可以用到路径压缩（让x直接指向祖先）

　　　　　　　　　　　　　　　　　　👇

int find(int x)
{
    if(fa[x]!=x)
    {
        fa[x]=find(fa[x]);
    }
    return fa[x];
}

并查集已经弄好了查就差并了。

我们并不在意谁是祖先那就让我们将x，y合并。

　　　　　　　　　  👇

 

void unionset(int x,int y)
{
    x=find(x);
    y=find(y);
    fa[x]=y;
}

 

然后将写好的模板带入如题目中还有二点值得注意：

一、初始化

　　将所有节点的父节点都设为自己，即fa[i]=i

二、连的边的个数

　　　　　　连的边数=区块数-1

那区块数怎么求呢？

我们将城市的序号遍历一遍，只要当前点的祖宗是自己，ans++，最后ans就是区块数了。

程序：

#include<bits/stdc++.h>
using namespace std;
const int maxn=1010;
int fa[maxn]={0},ans;
int find(int x)
{
    if(fa[x]!=x)
    {
        fa[x]=find(fa[x]);
    }
    return fa[x];
}

void unionset(int x,int y)
{
    x=find(x);
    y=find(y);
    fa[x]=y;
}
int main()
{
    for(;;)
    {
        int n,m;
        cin>>n;
        if(n==0) return 0;
        cin>>m;
        for(int i=1;i<=maxn;i++) fa[i]=i;
        for(int i=1;i<=m;i++)
        {
            int a,b;
            cin>>a>>b;
            unionset(b,a);
        }
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            if(find(i)==i) ans++;
        }
        cout<<ans-1<<endl;
    }
    return 0;
}