Cow Picnic S 更新了（在后面）

 

 

 解题思路： 从每头奶牛的节点开始做搜索，用dfs走遍所有路径（走到底，不回头）。每遍历到一个节点该节点遍历次数就加一，最后所有奶牛都搜索完之后，检查每个节点的遍历次数，如果该节点的遍历次数等于奶牛数则该节点能被所有奶牛走到。

坑：

1.每头奶牛搜索的时候要有清空的vis数组记录走没走过该点，否则可能路径会重复循环。

2.要用邻接矩阵mp[i][j]来记录节点的连接关系 ，其中i 是起点的编号 ， j  是终点的编号， 矩阵的值为1时表示i 到 j 可以连接，0表示没有。

#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int k,n,m,l[N]={0},vis[N]={0},mp[N][N]={0},vis1[N]={0}; 
void dfs(int x)
{
    vis1[x]=1;
    vis[x]++;
    for(int i=1;i<=n;i++)
    {
        if(mp[x][i]==1&&vis1[i]==0)
        {
            dfs(i);
        }
    }
}
int main()
{
    cin>>k>>n>>m;
    for(int i=1;i<=k;i++)
    {
        scanf("%d",&l[i]);
    }
    for(int i=1;i<=m;i++)
    {
        int a1,b;
        scanf("%d%d",&a1,&b);
        mp[a1][b]=1;
    }
    for(int i=1;i<=k;i++)
    {
        memset(vis1,0,sizeof(vis1));
        dfs(l[i]);
    } 
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(vis[i]==k) ans++;
    }
    cout<<ans<<endl;
    return 0;
}

 

更新了：

有优化方案：

新思路≈图存储方式、遍历方式优化

 就用一个vector（二维）来记录一个节点跟所有连接节点的关系。

还有亿个细节值得注意：

因为这里是有向表所以 edge[a1].push_back(b); 

如果是无向表 edge[a1].push_back(b); 2 edge[b].push_back(a1); 

以及dfs中的for循环要改一下。i的范围：  [0,edge[x].size()-1]

效果：

存储效率，循环效率更高

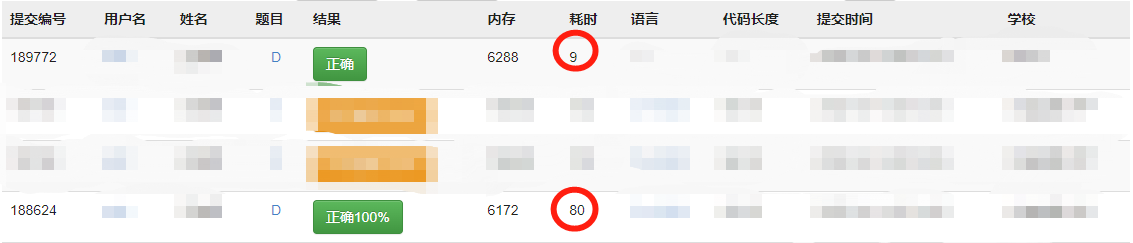
效果如图所示，提交编号为188624的为优化前的提交记录耗时80ms，提交编号为189772的为优化后的提交记录耗时9ms

 

 

程序：

#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int k,n,m,l[N]={0},vis[N]={0},mp[N][N]={0},vis1[N]={0}; 
vector<int> edge[N];
void dfs(int x)
{
    vis1[x]=1;
    vis[x]++;
    for(int i=0;i<edge[x].size();i++)
    {
        if(vis1[edge[x][i]]==0)
        {
            dfs(edge[x][i]);
        }
    }
}
int main()
{
    cin>>k>>n>>m;
    for(int i=1;i<=k;i++)
    {
        scanf("%d",&l[i]);
    }
    for(int i=1;i<=m;i++)
    {
        int a1,b;
        scanf("%d%d",&a1,&b);
        edge[a1].push_back(b);
    }
    for(int i=1;i<=k;i++)
    {
        memset(vis1,0,sizeof(vis1));
        dfs(l[i]);
    } 
    int ans=0;
    for(int i=1;i<=n;i++)
    {
        if(vis[i]==k) ans++;
    }
    cout<<ans<<endl;
    return 0;
}