软件工程第三次作业-结对项目
软件工程第三次作业——结对项目
| 这个作业属于哪个课程 | 班级的链接 |
|---|---|
| 这个作业要求在哪里 | 作业要求的链接 |
| 这个作业的目标 | 实现一个自动生成小学四则运算题目的命令行程序 |
作者:黄龙宇3122002625 赖柏源3123004146
Github项目地址: https://github.com/WiseL00k/software-engineering-2025-session-3/
一、PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 35 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 35 | 30 |
| Development | 开发 | 300 | 348 |
| · Analysis | · 需求分析 (包括学习新技术) | 40 | 50 |
| · Design Spec | · 生成设计文档 | 35 | 40 |
| · Design Review | · 设计复审 | 25 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 35 |
| · Design | · 具体设计 | 40 | 45 |
| · Coding | · 具体编码 | 70 | 85 |
| · Code Review | · 代码复审 | 30 | 35 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 30 | 38 |
| Reporting | 报告 | 73 | 93 |
| · Test Repor | · 测试报告 | 35 | 46 |
| · Size Measurement | · 计算工作量 | 18 | 22 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 25 |
| · 合计 | 408 | 471 |
二、设计实现过程
代码组织结构
本项目采用面向对象设计,通过多个类协同工作实现分数运算题目生成与自动批改功能。整体结构清晰,职责分明,各模块间低耦合高内聚。
核心类设计
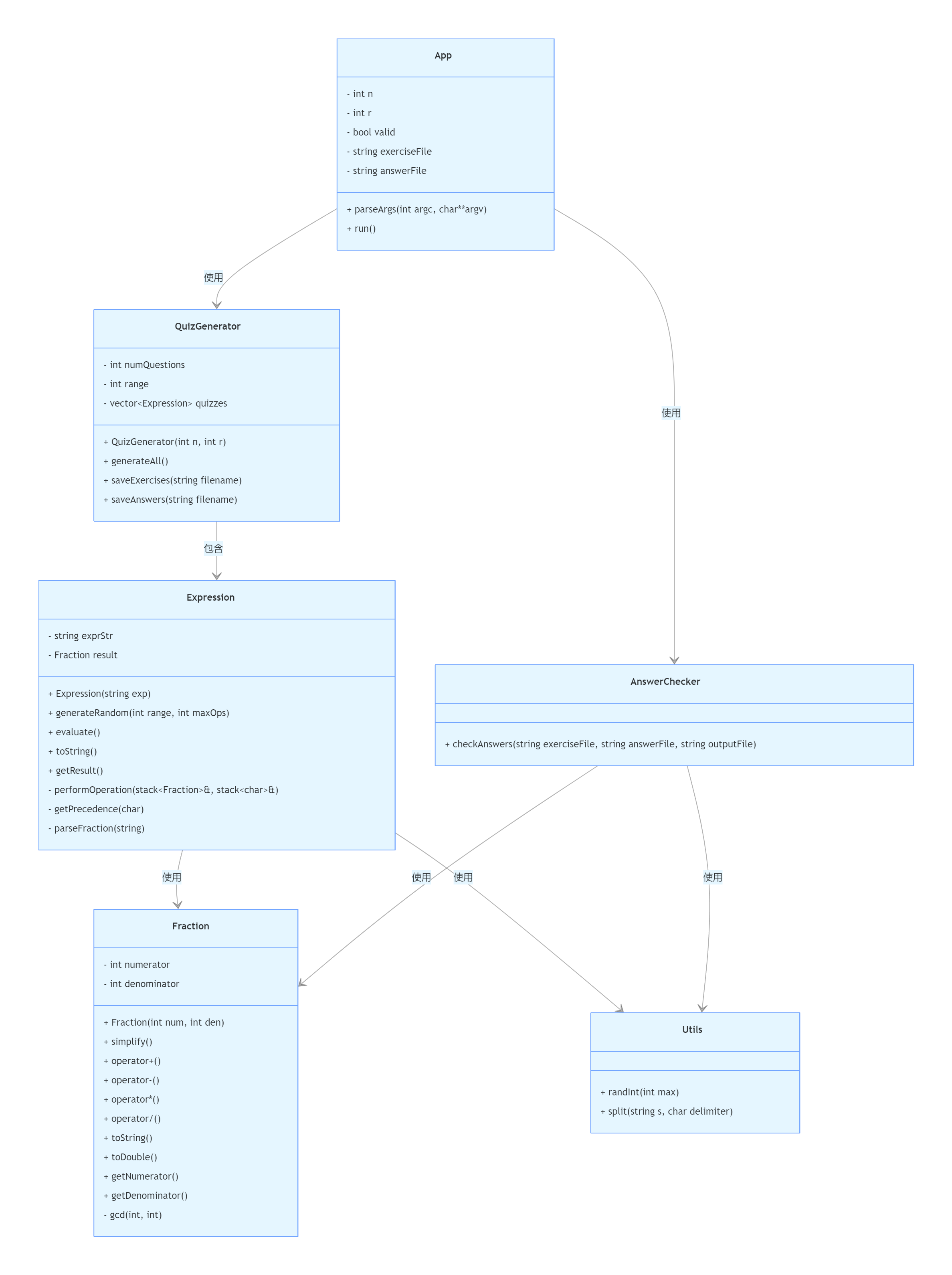
类关系说明
1.依赖关系:
App是程序入口,协调QuizGenerator和AnswerChecker工作QuizGenerator负责批量生成Expression对象Expression依赖Fraction进行数值计算,依赖Utils进行随机数生成AnswerChecker依赖Fraction进行答案比对,依赖Utils进行字符串处理
2.职责划分:
- 工具层 :
Utils提供通用功能(随机数、字符串分割) - 数据层 :
Fraction封装分数数据及运算 - 业务层 :
Expression处理表达式逻辑,QuizGenerator处理题目生成 - 控制层 :
App处理命令行参数和流程控制,AnswerChecker处理批改逻辑
| 模块 | 功能 | 主要职责 |
|---|---|---|
Fraction |
处理分数和四则运算 | 基础数据结构 |
Expression |
构建与计算单个算术表达式 | 表达式逻辑层 |
QuizGenerator |
批量生成题目与答案文件 | 题目管理层 |
AnswerChecker |
判定答案正确与否 | 检查与统计 |
Utils |
提供通用工具 | 支撑功能 |
App |
解析命令行并调度程序 | 主控制逻辑 |
关键函数流程图
1. Expression::generateRandom(随机生成表达式)
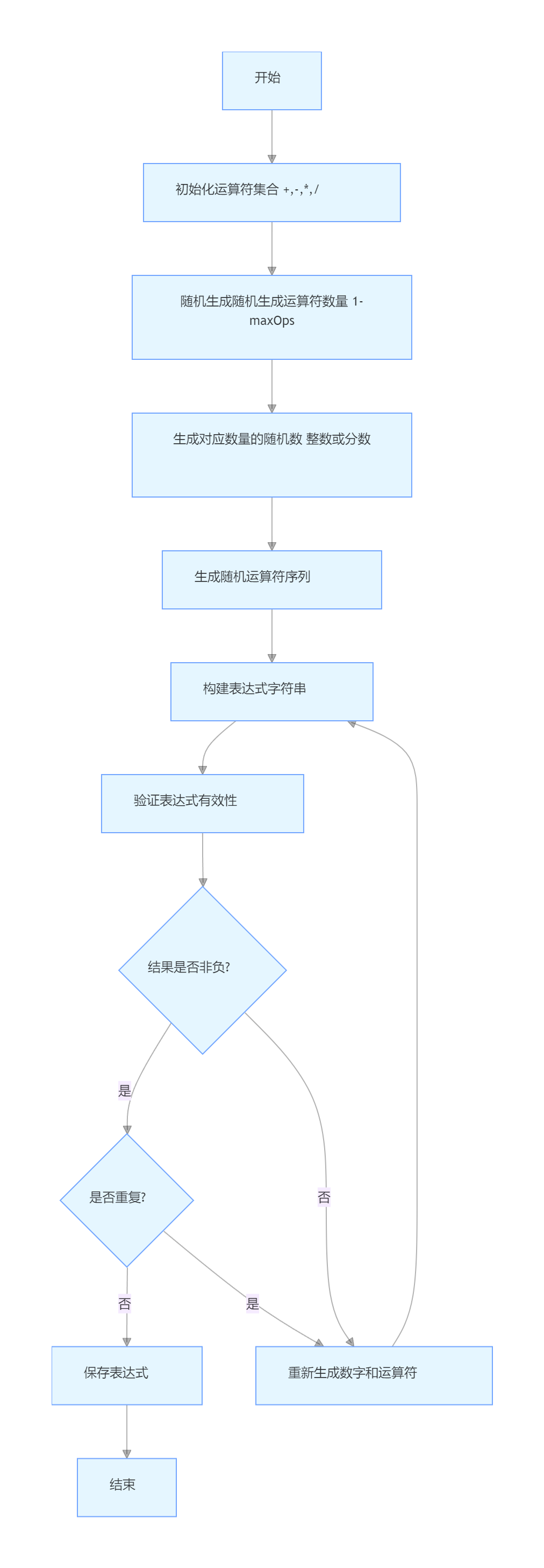
2. Expression::evaluate(表达式求值)
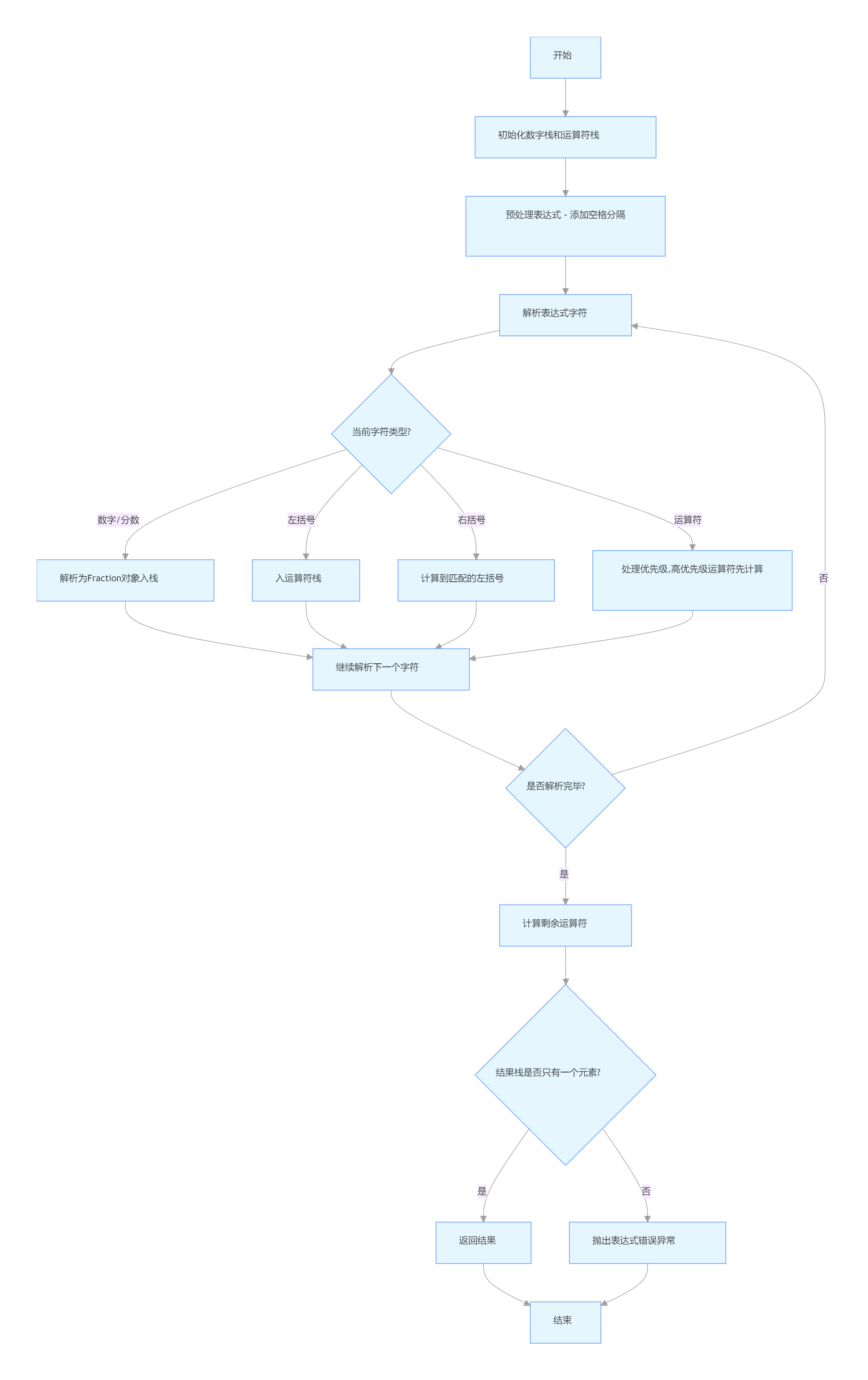
3. AnswerChecker::checkAnswers(答案校验)
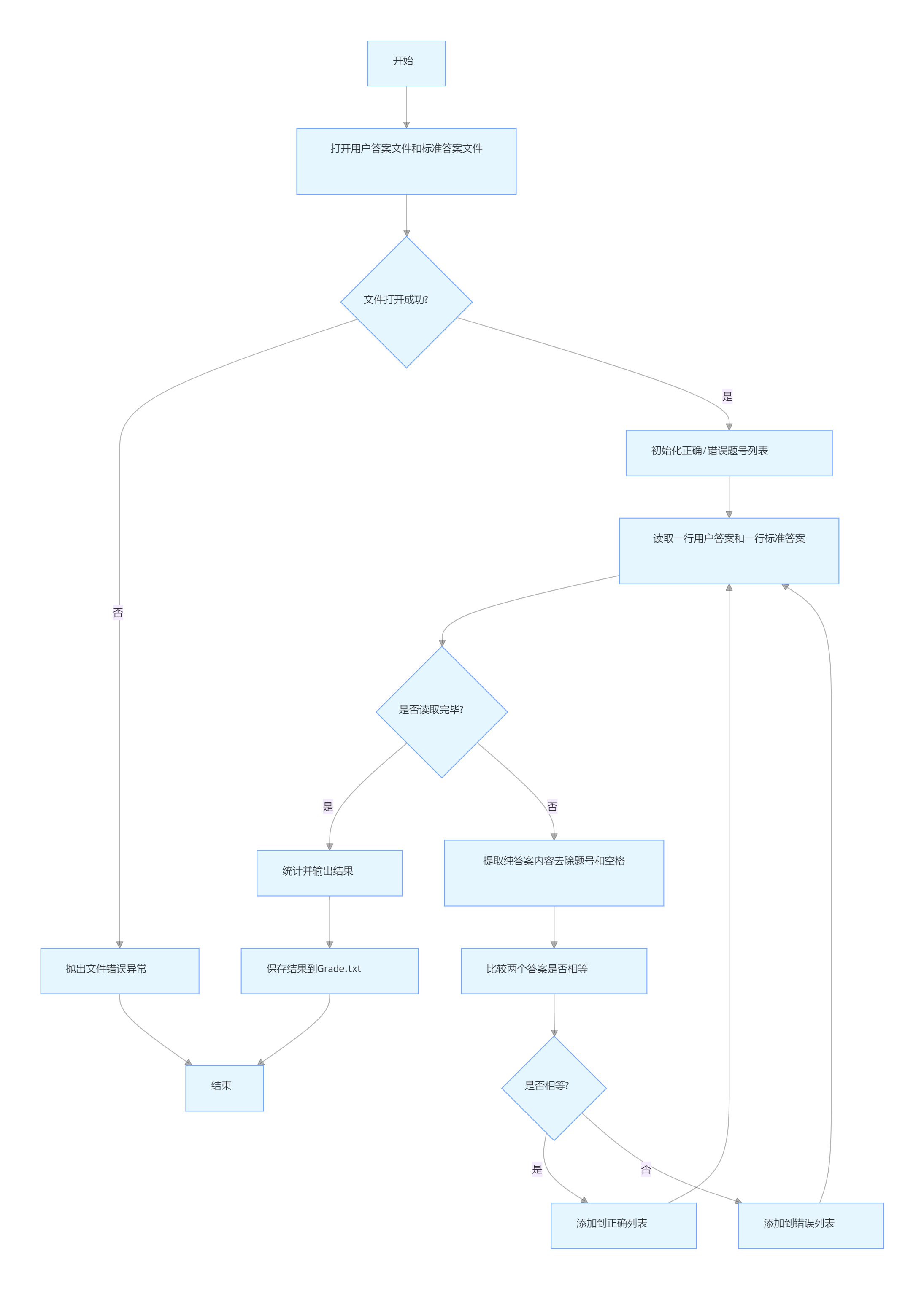
4. QuizGenerator::generateAll(批量生成题目)
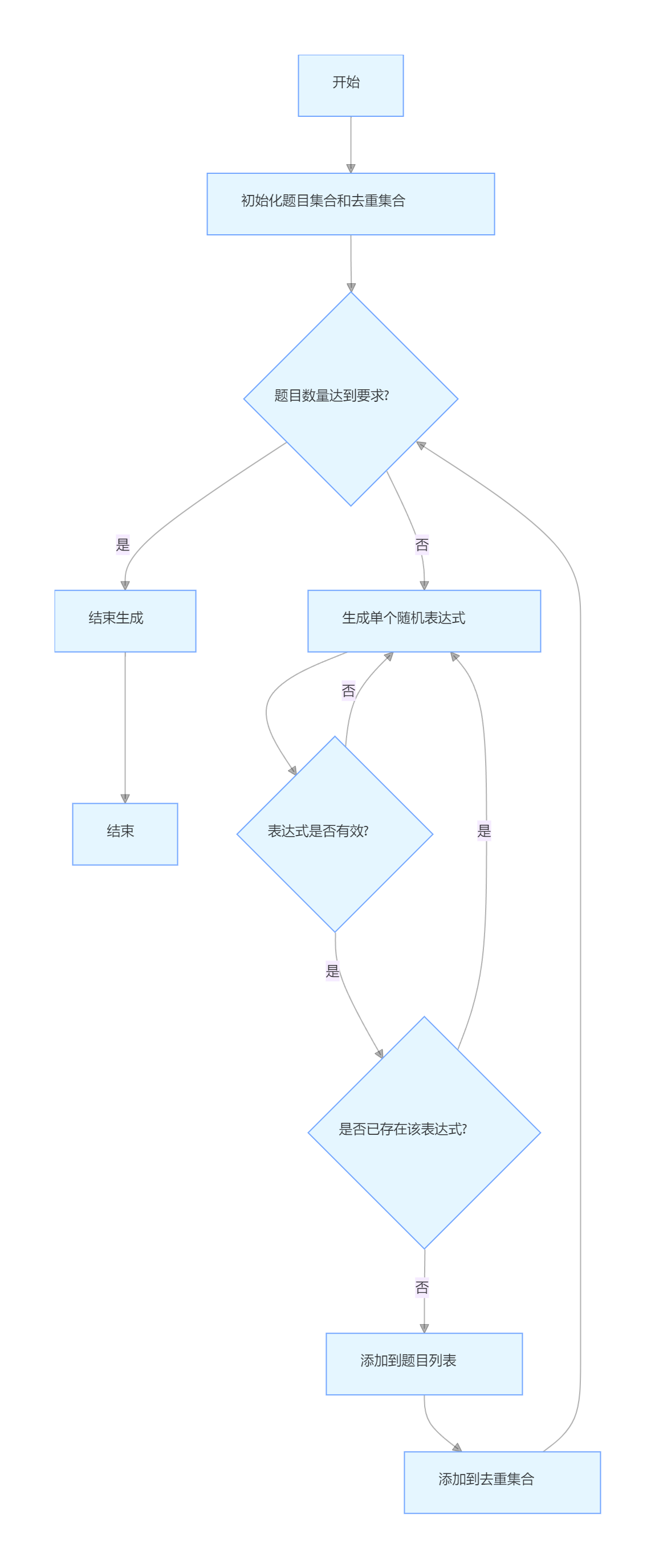
核心函数说明
1.Expression::generateRandom:
负责生成符合要求的随机表达式,确保结果非负、无重复,通过多次尝试机制处理无效表达式
2.Expression::evaluate:
使用双栈算法(数字栈和运算符栈)解析并计算表达式,处理运算符优先级,确保计算正确性
3.Fraction 类运算重载:
实现分数的四则运算,自动化简结果,确保分母为正数,处理除法中的除零错误
4.AnswerChecker::checkAnswers:
对比用户答案与标准答案,支持整数、真分数和带分数三种格式,先字符串比对再解析为分数比对
5.QuizGenerator::generateAll:
批量生成指定数量的不重复表达式,使用集合进行去重管理,限制最大尝试次数避免无限循环
三、代码说明
1. Fraction 类核心实现(分数处理基础)
分数类是整个系统的基础数据结构,负责分数的表示、运算和格式化,确保所有数值计算的准确性。
// 分数化简实现
void Fraction::simplify() {
// 特殊情况:分子为0时,固定分母为1(0/1)
if (numerator == 0) {
denominator = 1;
return;
}
// 计算分子分母的最大公约数(GCD),用于化简
int common = gcd(numerator, denominator);
numerator /= common; // 分子除以最大公约数
denominator /= common; // 分母除以最大公约数
// 确保分母始终为正数(若分母为负,分子分母同时取反)
if (denominator < 0) {
numerator = -numerator;
denominator = -denominator;
}
}
思路说明:
化简是分数运算的核心需求,通过最大公约数(GCD)实现分数的最简表示,避免同一分数的不同形式(如 2/4 和 1/2)被误认为不同值。同时强制分母为正数,保证表示的唯一性。
// 减法运算重载(确保结果非负)
Fraction Fraction::operator-(const Fraction& other) const {
// 分数减法公式:a/b - c/d = (ad - bc)/bd
int newNum = numerator * other.denominator - other.numerator * denominator;
int newDen = denominator * other.denominator;
Fraction result(newNum, newDen); // 先构造临时结果
// 核心约束:小学生题目不允许负数结果,抛出异常过滤无效表达式
if (result.toDouble() < 0) {
throw runtime_error("减法结果不能为负数");
}
return result;
}
思路说明:重载减法运算符时,不仅实现数学运算,还加入了业务约束 —— 确保结果非负。通过异常机制,在生成表达式时可直接过滤掉不符合要求的减法运算(如 3-5)。
// 分数转字符串(支持带分数表示)
string Fraction::toString() const {
// 整数情况(分母为1):直接返回分子
if (denominator == 1) {
return to_string(numerator);
}
// 真分数情况(分子绝对值 < 分母):格式为“分子/分母”
if (abs(numerator) < denominator) {
return to_string(numerator) + "/" + to_string(denominator);
}
// 带分数情况(分子绝对值 >= 分母):格式为“整数'分子/分母”
else {
int whole = numerator / denominator; // 提取整数部分
int remainder = abs(numerator % denominator); // 提取剩余分子(取绝对值)
if (remainder == 0) {
return to_string(whole); // 若剩余分子为0,直接返回整数
}
return to_string(whole) + "'" + to_string(remainder) + "/" + to_string(denominator);
}
}
思路说明:根据分数的实际大小,自动转换为最符合小学生习惯的表示形式(整数、真分数、带分数),例如将 3/2 转换为 “1'1/2”,提高题目可读性。
2. 表达式生成与计算(核心业务逻辑)
Expression 类负责随机生成符合要求的数学表达式,并计算结果,是连接分数运算与题目生成的关键。
// 随机生成表达式
void Expression::generateRandom(int range, int maxOps) {
vector<char> ops = {'+', '-', '*', '/'}; // 支持的运算符
// 随机生成运算符数量(1到maxOps个,确保表达式有运算)
int numOperators = Utils::randInt(maxOps) + 1;
int numNumbers = numOperators + 1; // 数字数量 = 运算符数量 + 1
vector<Fraction> numbers; // 存储表达式中的数字
vector<char> operators; // 存储表达式中的运算符
// 生成数字(整数或分数)
for (int i = 0; i < numNumbers; i++) {
// 50%概率生成整数,50%概率生成真分数
if (Utils::randInt(2) == 0) {
// 生成整数:范围[0, range),且避免除数为0(i>0时数字可能作为除数)
int num;
do {
num = Utils::randInt(range);
} while (num == 0 && i > 0); // i=0时允许0(作为被减数/被除数)
numbers.push_back(Fraction(num, 1));
} else {
// 生成真分数:分母范围[2, range),分子范围[1, 分母-1]
int denom = Utils::randInt(range - 2) + 2; // 确保分母>=2
int numer = Utils::randInt(denom - 1) + 1; // 确保分子<分母
numbers.push_back(Fraction(numer, denom));
}
}
// 生成运算符序列
for (int i = 0; i < numOperators; i++) {
int opIndex = Utils::randInt(ops.size()); // 随机选择运算符
operators.push_back(ops[opIndex]);
}
// 构建表达式字符串(数字与运算符交替拼接,中间加空格分隔)
stringstream ss;
for (int i = 0; i < numNumbers; i++) {
ss << numbers[i].toString(); // 拼接数字
if (i < numOperators) {
ss << " " << operators[i] << " "; // 拼接运算符(加空格分隔)
}
}
exprStr = ss.str(); // 保存表达式字符串
// 验证表达式有效性(最多尝试5次,避免无限循环)
int attempts = 0;
while (attempts < 5) {
try {
result = evaluate(); // 计算表达式结果
if (result.toDouble() >= 0) break; // 确保结果非负
} catch (...) {
// 若计算失败(如负数结果、除零等),重新生成表达式
// (省略重新生成数字和运算符的代码,逻辑同上)
}
attempts++;
}
}
思路说明:
表达式生成采用 “分步随机 + 验证过滤” 策略:先随机生成数字和运算符,再通过计算验证表达式是否有效(结果非负、无除零等)。通过限制最大尝试次数,平衡随机性和程序稳定性,确保能生成足够数量的有效题目。
3. 答案校验实现(自动批改核心)
答案校验是实现自动批改的关键,需要处理多种格式的答案输入,并准确判断是否与标准答案一致。
// 比较用户答案与标准答案
bool compareAnswers(const string& userAnswer, const string& correctAnswer) {
string userAns = userAnswer;
string correctAns = correctAnswer;
// 预处理:移除所有空格,兼容用户输入时的空格(如“1 / 2”和“1/2”视为相同)
userAns.erase(remove(userAns.begin(), userAns.end(), ' '), userAns.end());
correctAns.erase(remove(correctAns.begin(), correctAns.end(), ' '), correctAns.end());
// 快速校验:若字符串完全一致,直接返回正确
if (userAns == correctAns) {
return true;
}
// 深度校验:解析为Fraction对象后比较(处理等价分数,如2/4和1/2)
try {
Fraction userFrac, correctFrac;
// 解析用户答案为Fraction对象
if (userAns.find('/') != string::npos) { // 包含“/”,是分数
if (userAns.find('\'') != string::npos) { // 包含“'”,是带分数(如1'1/2)
size_t apostrophePos = userAns.find('\'');
int whole = stoi(userAns.substr(0, apostrophePos)); // 提取整数部分
string fracPart = userAns.substr(apostrophePos + 1); // 提取分数部分
size_t slashPos = fracPart.find('/');
int numer = stoi(fracPart.substr(0, slashPos)); // 提取分子
int denom = stoi(fracPart.substr(slashPos + 1)); // 提取分母
// 转换为假分数:整数*分母 + 分子
userFrac = Fraction(whole * denom + numer, denom);
} else { // 真分数(如3/4)
size_t slashPos = userAns.find('/');
int numer = stoi(userAns.substr(0, slashPos));
int denom = stoi(userAns.substr(slashPos + 1));
userFrac = Fraction(numer, denom);
}
} else { // 整数(如5)
userFrac = Fraction(stoi(userAns), 1);
}
// 解析标准答案为Fraction对象(逻辑同上,省略重复代码)
// ...
// 关键:化简后比较分子和分母,确保等价分数判定为正确
userFrac.simplify();
correctFrac.simplify();
return userFrac.getNumerator() == correctFrac.getNumerator() &&
userFrac.getDenominator() == correctFrac.getDenominator();
} catch (...) {
// 若解析失败(如格式错误),判定为错误
return false;
}
}
思路说明:答案校验采用 “双重校验” 策略:先通过字符串比对快速判断完全一致的情况;再通过解析为分数对象并化简,处理等价分数(如 2/4 和 1/2)的判定。同时兼容多种输入格式(带空格、整数、真分数、带分数),提高用户体验。异常处理确保格式错误的答案被正确判定为错误。
四、测试运行
基本功能测试
生成题目功能
生成10道题目,且自然数范围为0-10
测试结果
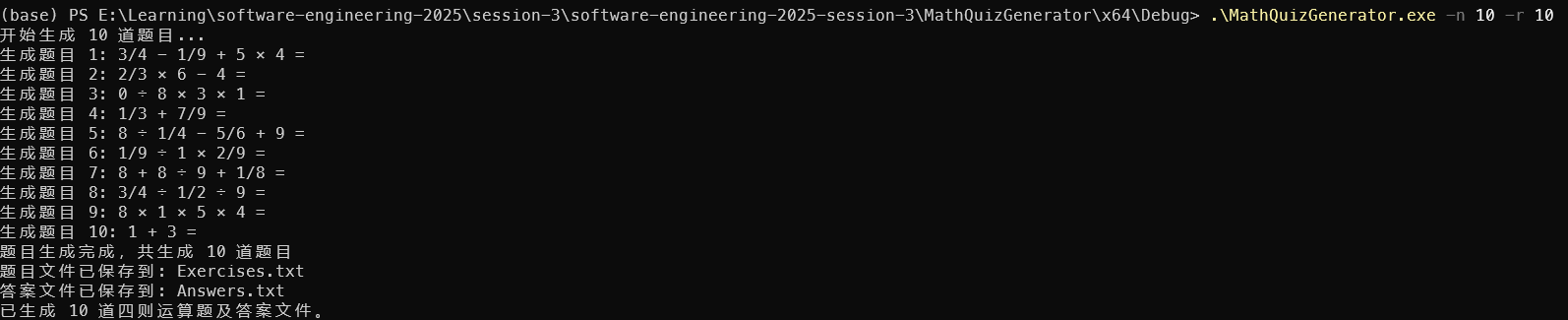
生成50道题目,且自然数范围为0-8
测试结果
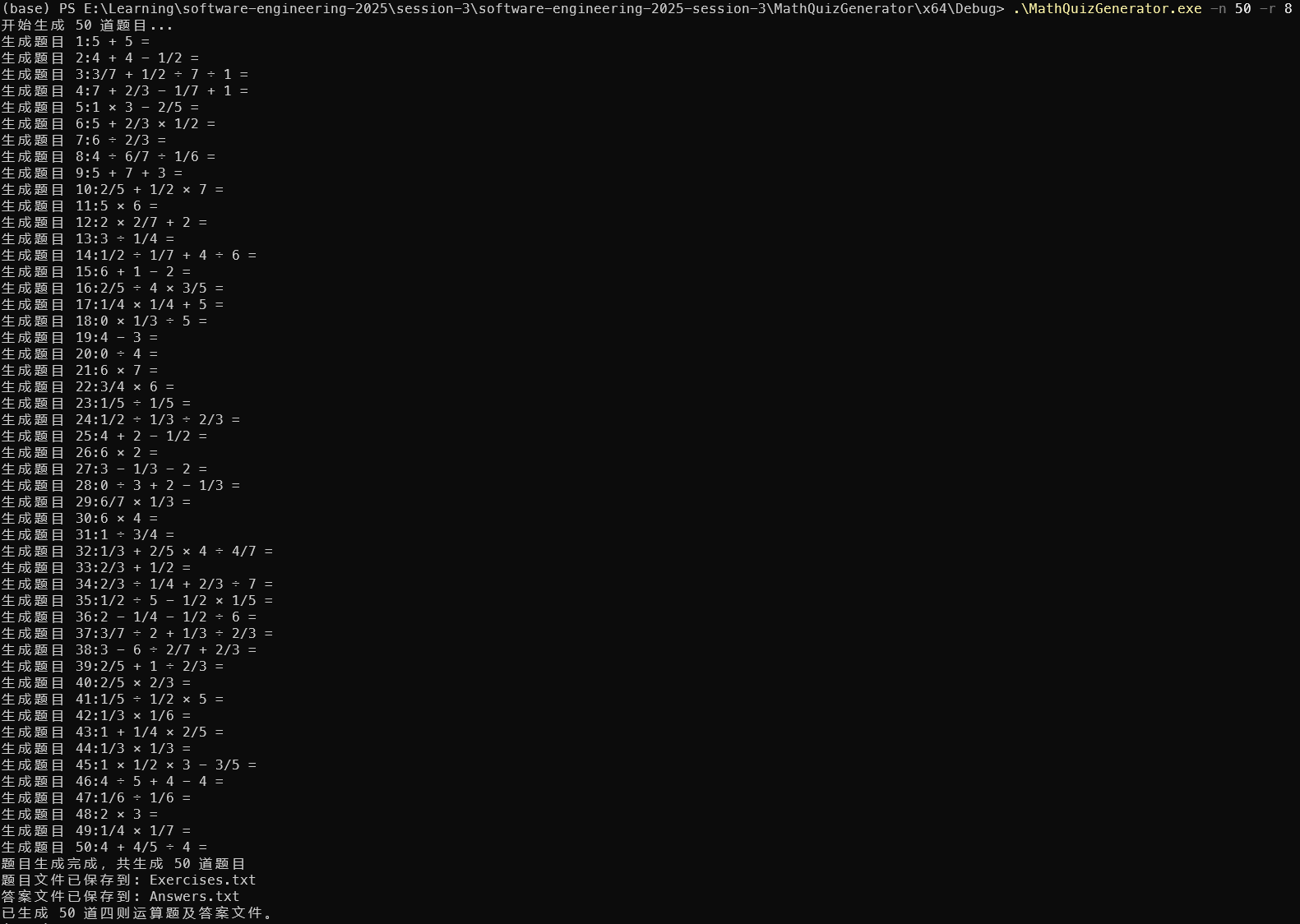
极限情况测试
生成10000道题目,自然数范围为0-10
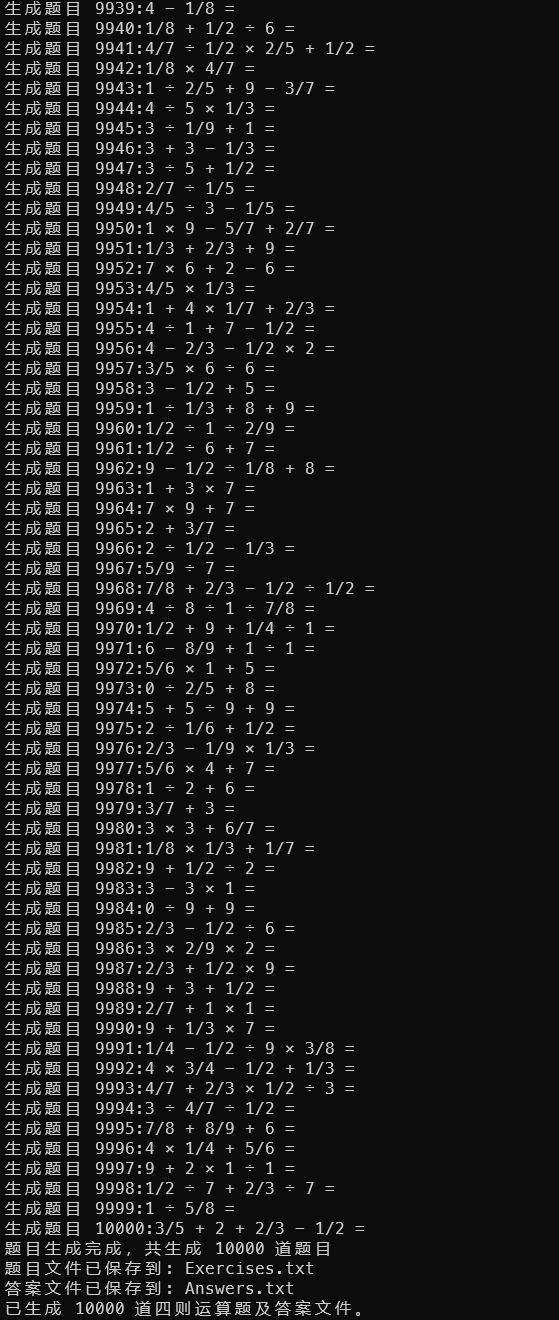
性能分析
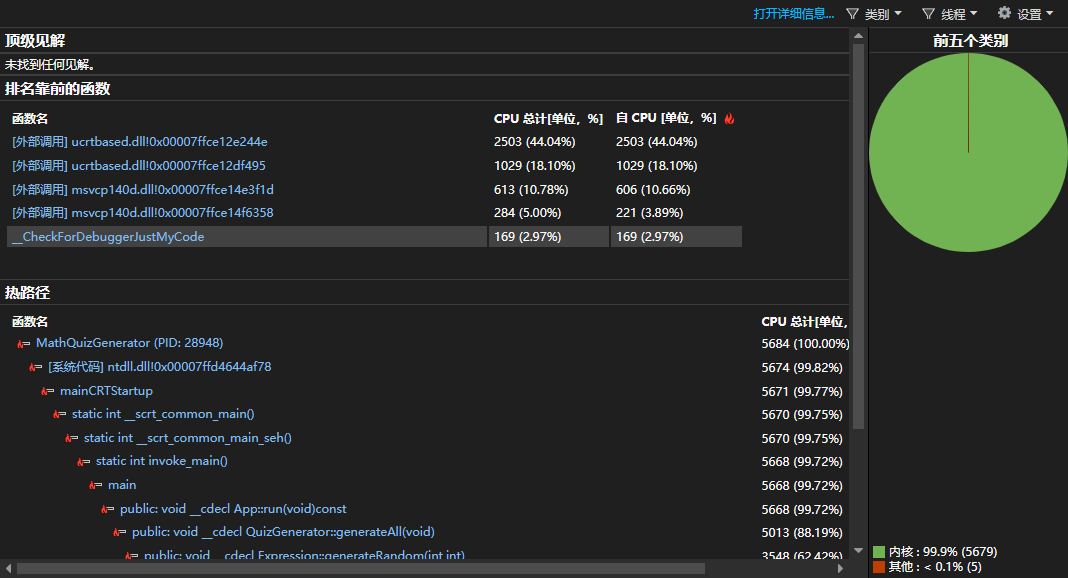
可以发现最耗时的函数是evalute函数,用于计算表达式的值
批改题目功能
题目文件
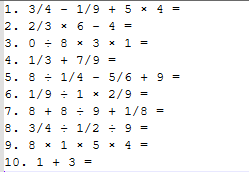
测试答案文件
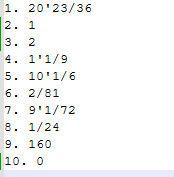
正确答案文件
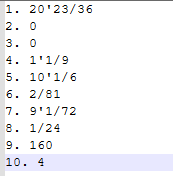
测试结果
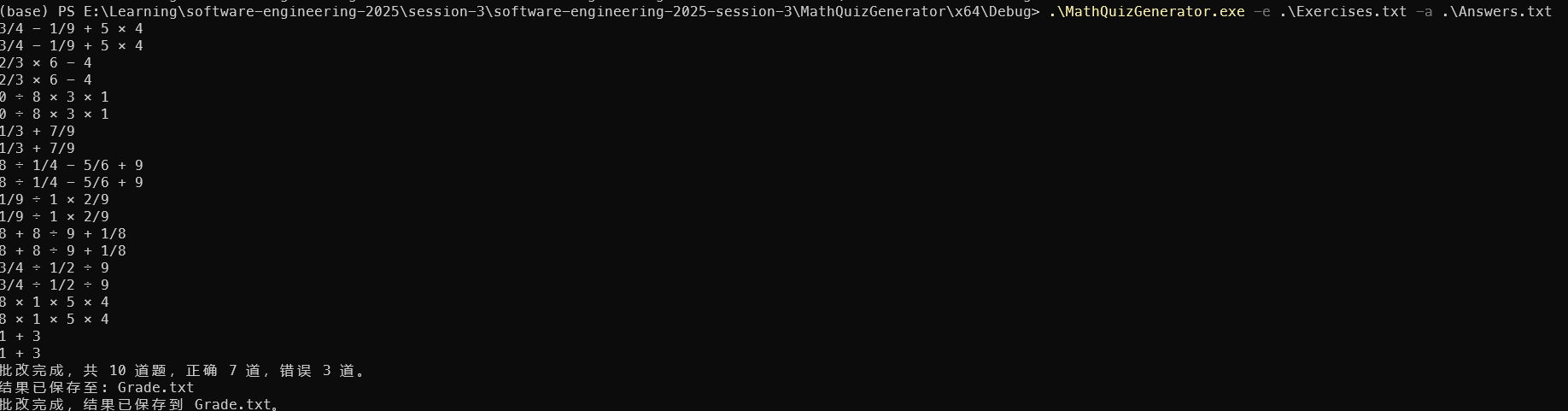
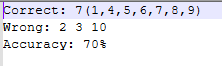
性能分析
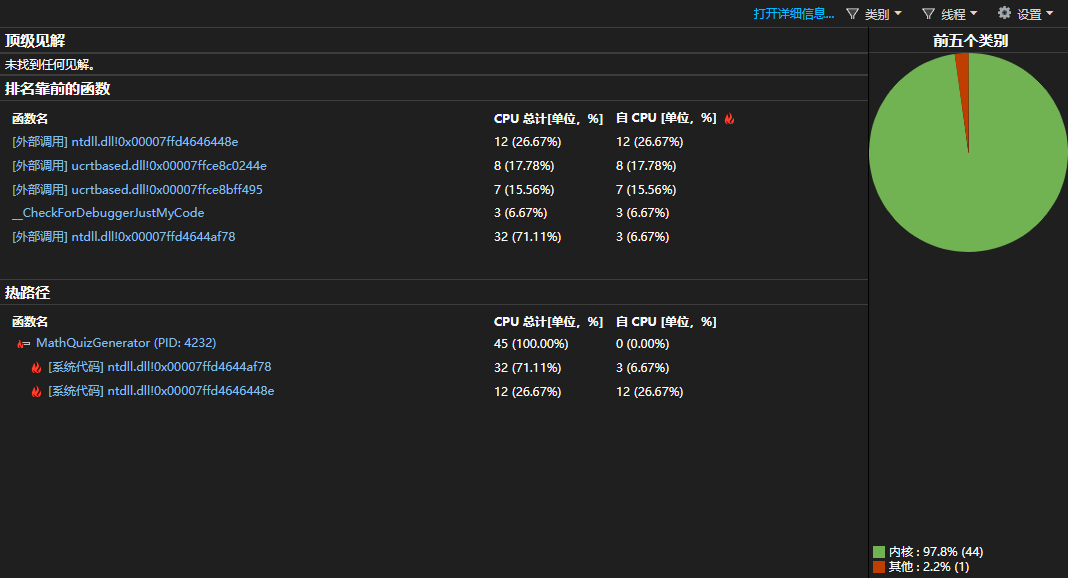
同样可以发现最耗时的函数是evalute函数,用于计算表达式的值
五、项目小结
- 模块化设计降低耦合,提升开发效率
- 项目严格按照 “基础层(Fraction/Utils)→ 业务层(Expression/QuizGenerator/AnswerChecker)→ 控制层(App)” 分层设计,各模块职责单一、接口清晰。例如Fraction类封装所有分数运算逻辑,Expression类仅依赖Fraction的接口即可实现表达式计算,无需关注分数内部实现。
- 异常处理与约束校验确保题目合法性
- Fraction类减法运算中,通过异常机制过滤负数结果(如 3-5);
- Expression类生成表达式时,避免除数为 0、连续除法等无效情况;
- AnswerChecker类支持多种答案格式(带空格、整数 / 分数 / 带分数),通过 “字符串比对 + 分数化简比对” 双重校验确保批改准确性。
- 互补性提升代码质量
- 问题解决效率更高
- 风险共担减少延误
- Github协同开发
通过github协同开发,提升了开发效率,便于版本回溯。

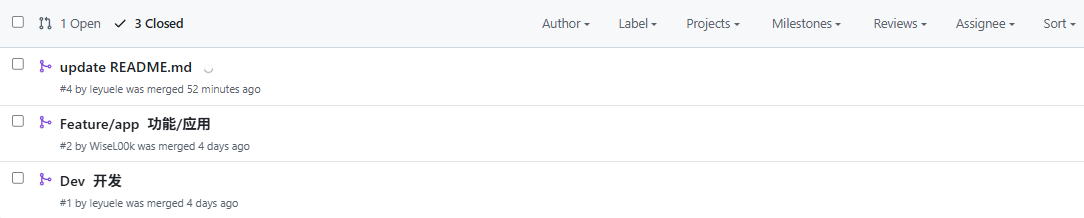
通过多个分支对应不同版本,在测试通过后,再合并到dev分支,最后总业务功能基本测试无误后,合并到main主分支,并发布Release版本
本次结对项目不仅完成了功能需求,更让我们深刻体会到 “1+1>2” 的协作价值 —— 通过优势互补、风险共担,既提升了代码质量,又提高了开发效率。同时,项目中的不足也为后续开发积累了宝贵经验:需求确认要严谨、接口约定要清晰、



 浙公网安备 33010602011771号
浙公网安备 33010602011771号