P2221 [HAOI2012]高速公路 题解

这是一道非常适合像蒟蒻一样想提升线段树水平的题目。

题目链接

题目大意

首先，我们要搞清楚让我们求什么，期望非常高大上，但是在这里其实就是求 \(l\) 到 \(r\) 任意选取两个点的所有方案的代价相加后除以总方案数，取一个平均值。

推理式子

接下来，我们细致考虑到每一条边。

例如对于图中的 \(i\rightarrow i+1\) 这条边:

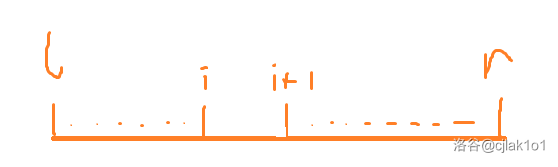
经过思考以后，我们发现在 \(l\) 到 \(r\) 这段区间中，它会参与代价的情况是两个收费站一个在 \(i\) 以及 \(i\) 的左边，同理，另一个在 \(i+1\) 以及 \(i+1\) 的右边。

所以它的贡献就是 \((i-l+1)* (r-i)* dis[i][i+1]\) 。

我们在把每一条边的贡献加起来，并以 \(i\) 的降幂排序有关将式子转化为我们要的式子。

(由于 \(i\) 是我们取的边的左端点，所以 \(i\) 从 \(l\) 遍历到 \(r-1\))

\[\sum\limits_{i=l}^{r-1}(i-l+1)* (r-i)* dis[i][i+1] \]

\[\Longrightarrow \sum\limits_{i=l}^{r-1}(-i^2+ri+li-i-lr+r)* dis[i][i+1] \]

\[\Longrightarrow -\sum\limits_{i=1}^{r-1}i^2* dis[i][i+1]+(r+l-1)\sum\limits_{i=1}^{r-1} i* dis[i][i+1]+r(1-l)\sum\limits_{i=1}^{r-1}dis[i][i+1] \]

线段树维护

我们现在已经得到了式子，又因为这道题是区间修改，区间查询，所以我们会联想到线段树。

• 区间修改

我们设 \(sum1,sum2,sum3\)。

\(sum1=\sum\limits_{i=l}^{r-1}i^2* dis[i][i+1]\)
\(sum2=\sum\limits_{i=l}^{r-1}i* dis[i][i+1]\)
\(sum3=\sum\limits_{i=l}^{r-1}dis[i][i+1]\)

\(sum3\) 的改变只需要加上长度乘以 \(v\)。

\(sum2\) 的改变利用等差数列求和乘以 \(v\)。

\(sum1\) 的改变利用平方和公式求和乘以 \(v\)。

具体见代码。

• 区间查询

把对应区间的 \(sum1,sum2,sum3\) 求出，然后套式子求出代价和，求其与方案数的 \(gcd\) 输出答案。

code

#include<bits/stdc++.h>
#define int long long
#define ls rt<<1
#define rs rt<<1|1
#define lson ls,l,mid
#define rson rs,mid+1,r
using namespace std;
const int N=1e5+1e3;

int read(){
	int res=0,f=1;char c;
	for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
	for(;isdigit(c);c=getchar()) res=(res<<1)+(res<<3)+(c^48);
	return res*f;
}

int n,m;
struct TREE{
	int sum1,sum2,sum3;
	int lazy;
}t[N<<2];
char op;

int count1(int l,int r){return (l+r)*(r-l+1)/2;}//等差数列求和
int count2(int l,int r){return (r)*(r+1)*(2*r+1)/6-(l-1)*(l-1+1)*(2*(l-1)+1)/6;}//平方和求和

void push_down(int rt,int l,int r){
	if(t[rt].lazy!=0){
		int mid=(l+r)>>1,v=t[rt].lazy;
		t[ls].lazy+=t[rt].lazy,t[rs].lazy+=t[rt].lazy;
		t[ls].sum1+=(mid-l+1)*v;t[rs].sum1+=(r-mid)*v;
		t[ls].sum2+=count1(l,mid)*v;t[rs].sum2+=count1(mid+1,r)*v;
		t[ls].sum3+=count2(l,mid)*v;t[rs].sum3+=count2(mid+1,r)*v;
		t[rt].lazy=0;
	}
}

void push_up(int rt){
	t[rt].sum1=t[ls].sum1+t[rs].sum1;
	t[rt].sum2=t[ls].sum2+t[rs].sum2;
	t[rt].sum3=t[ls].sum3+t[rs].sum3;
}

void update(int rt,int l,int r,int ul,int ur,int v){
	if(ul<=l&&r<=ur){
		t[rt].sum1+=(r-l+1)*v;
		t[rt].sum2+=count1(l,r)*v;
		t[rt].sum3+=count2(l,r)*v;
		t[rt].lazy+=v;
		return;
	}
	push_down(rt,l,r);
	int mid=(l+r)>>1;
	if(ul<=mid) update(lson,ul,ur,v);
	if(mid<ur) update(rson,ul,ur,v);
	push_up(rt);
}

void query(int rt,int l,int r,int ql,int qr,int &sum1,int &sum2,int &sum3){
	if(ql<=l&&r<=qr){
		sum1+=t[rt].sum1,sum2+=t[rt].sum2,sum3+=t[rt].sum3;
		return;
	}
	push_down(rt,l,r);
	int mid=(l+r)>>1,res=0;
	if(ql<=mid) query(lson,ql,qr,sum1,sum2,sum3);
	if(mid<qr) query(rson,ql,qr,sum1,sum2,sum3);
	return;
}

signed main(){
	n=read(),m=read();
	//build(1,1,n);蒟蒻不太想build
	for(int i=1;i<=m;i++){
		cin>>op;
		if(op=='C'){
			int ul=read(),ur=read(),v=read();
			update(1,1,n,ul,ur-1,v);
		}
		else{
			int ql=read(),qr=read(),sum1=0,sum2=0,sum3=0;
			query(1,1,n,ql,qr-1,sum1,sum2,sum3);
			int sum=(qr-ql+1)*(qr-ql)/2,val=-sum3+(qr+ql-1)*sum2-qr*(ql-1)*sum1;
			int gcd=__gcd(val,sum);
			printf("%lld/%lld\n",val/gcd,sum/gcd);
		}
	}
	return 0;
}
/*
4 5
C 1 4 2
C 1 2 -1
Q 1 2
Q 2 4
Q 1 4
*/