蒟蒻的提高组复习——字符串

字符串

---

1.字符串基础

类型

• 字符集
• 字符串
• 子串
• 子序列
• 前缀,真前缀
• 后缀,真后缀
• 字典序
• 回文串

存储

• char
• string

2.字符串匹配

简介

又称模式匹配（pattern matching）。该问题可以概括为「给定字符串\(S\)和\(T\) ，在主串\(S\)中寻找子串\(T\)」。字符\(T\)称为模式串 (pattern)。

类型

单串匹配：给定一个模式串和一个待匹配串，找出前者在后者中的所有位置。
多串匹配：给定多个模式串和一个待匹配串，找出这些模式串在后者中的所有位置。
出现多个待匹配串时，将它们直接连起来便可作为一个待匹配串处理。
可以直接当做单串匹配，但是效率不够高。
其他类型：例如匹配一个串的任意后缀，匹配多个串的任意后缀……

1.暴力

char s[maxn],t[maxn];//
int slen=strlen(s),tlen=strlen(t);
int i,j;
for(i=0;i<slen-tlen+1;i++)
	for(j=0;j<tlen;j++)
   	  if(s[i+j]!=t[j]) break;
if(j==tlen) puts("Yes");

2.hash

此处省略一万字

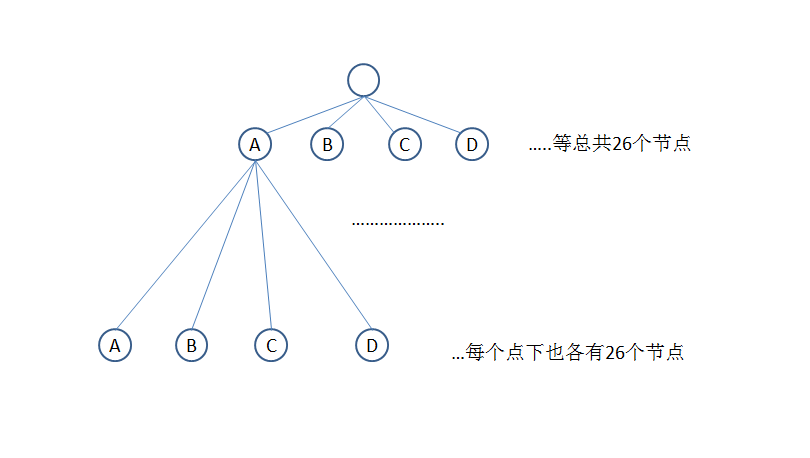
3.字典树(trie)

字典树，就是定义一个26叉树，每个节点的权为1(有'\(a\)'+i-1)或0(无)

inline void build(char a[])
{
        int k=1,l=strlen(a);
	for(int i=0;i<l;i++)
	{
		int id=a[i]-'A'+1;
		if(!f[k].nxt[id])
			f[k].nxt[id]=++sz;
		k=f[k].nxt[id];
	}
}

4.前缀函数与kmp算法

前缀函数的定义

给定一个长度为\(n\)的字符串\(s\)，其前缀函数被定义为一个长度为n的数组\(\pi\)。
\(\pi[i]\)的定义为：

1.如果子串\(s[0...i]\)有一对相等的真前缀和真后缀：\(s[0...k-1]\)和\(s[i-(k-1)...i]\),那么\(\pi[i]\)就等于这个真前缀的长度，即为k。
2.如果有不只一对相等的，那么\(\pi[i]\)就等于其中最长的真前缀长度。
3.如果没有想等的，\(\pi[i]\)=0。
4.\(\pi[0]\)=0。

简单来说，\(\pi[i]\)是子串\(s[0...i]\)最长的相等的真前缀与真后缀的长度

数学语言：

计算前缀函数的朴素算法

一个直接按照定义计算前缀函数的算法流程：

1.在一个循环中以\(i=1\rightarrow n-1\)的顺序计算\(\pi[i]\)的值。
2.我们让\(j\)从最大的真前缀长度\(i\)开始试。

for(int i=1;i<=n-1;i++)
	for(int j=i;j>=1;j--){
		int k;
  			for(k=1;k<=j;k++)
				if(s[k]!=s[n-k+1]) break;
		if(k==j)
		{
			pi[i]=j;
			break;
	    }     
   }

计算前缀函数的高效算法