Manacher 讲义

引入

当你遇到一道题：给定一个长度为 \(n\) 的字符串 \(s\)，让你找到所有对 \((i, j)\) 使得子串 \(s[i \dots j]\) 为一个回文串．当 \(t = t_{\text{rev}}\) 时，字符串 \(t\) 是一个回文串（\(t_{\text{rev}}\) 是 \(t\) 的反转字符串）。你会怎么做？

显然，在最坏情况下，最多可能会有 \(n ^ 2\) 个回文串，因此一眼望去该问题并没有线性解法。退而求其次，如果就只想暴力骗一点分，该怎么做呢？那这就简单了，我们可以通过“中心拓展法”来暴力。

中心拓展法

我们可以把一个字符串 \(S\) 的每个字符或每 \(2\) 个相同的字符看成中心，然后左右扩展检查，判断它左右的对称位置是否相同，若相同则是回文的一部分，直到对称位置不同为止。

那么它的效率如何呢？

若 \(S\) 中几乎没有长度大于 \(1\) 的回文串。检查每个字符的对称位置时，只需要比较左右各一个邻居字符就发现不同，停止检查。\(S\) 中的 \(n\) 个字符，总共只检查 \(n\) 次就够了，复杂度为 \(O(n)\)。这种情况下，中心扩展法很好，但这种情况很少见。

若 \(S\) 中有大量回文串，且长度较长。

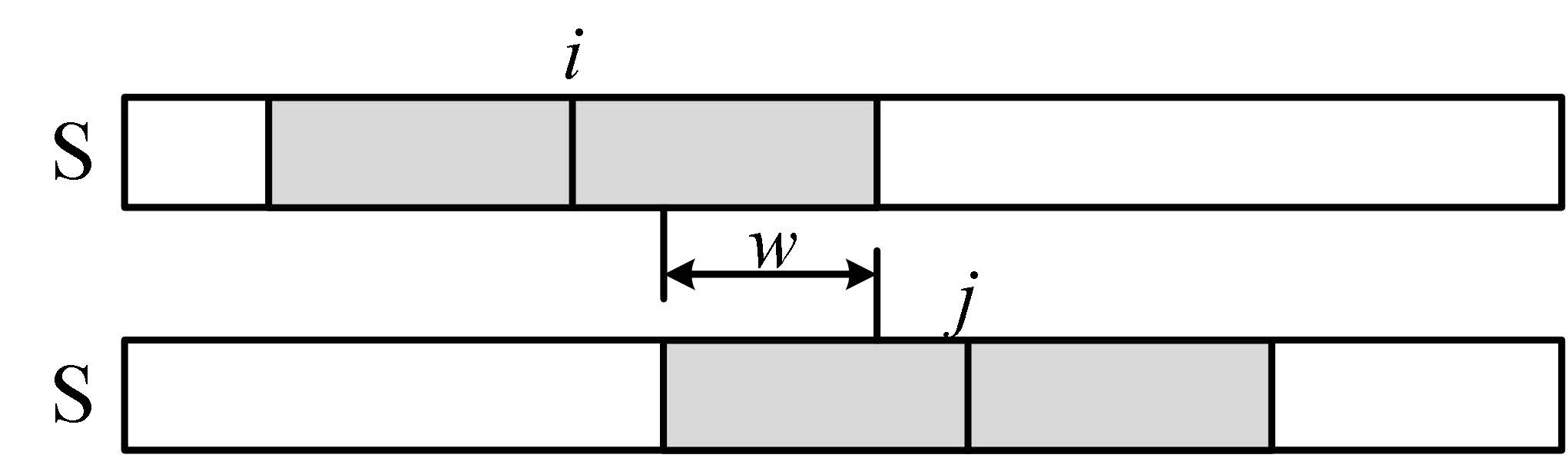
如图中，当检查到 \(i\) 时，以 \(i\) 为中心点扩展左右的邻居，最后得到阴影所示的回文串，这次检查是 \(O(n)\) 的。当检查到 \(j\) 时，同理也是 \(O(n)\) 的。\(S\) 中共 \(n\) 个字符，检查 \(n\) 次，总复杂度 \(O(n^2)\)，效率就低了。

如果能改善这种重复，就能设计出一个高效的算法。接下来，让我们研究研究，如何改善这种重复。

知识梳理

解决回文串问题有很多种解法：应用字符串哈希，该问题可在 \(O(n \log n)\) 时间内解决，而使用后缀数组和快速 LCA 该问题可在 \(O(n)\) 的时间复杂度内解决，但这些都和复杂。接下来描述的算法压倒性的简单，并且在时间和空间复杂度上具有更小的常数．该算法由 Glenn K. Manacher 在 1975 年提出，叫做 Manacher 算法。

Manacher

我们来对 \(S\) 做一个变换以简化问题。

我们可以发现，回文串有两种，一种长度为奇数，有一个中心字符，如 qwq 中的 w；一种长度为偶数，有两个相同的中心字符（或看作没有），如 hooh 中的 oo。如果这样，我们就需要讨论两次，用一个小技巧统一成一种情况：

• 在 \(S\) 的每个字符左右插入一个不属于 \(S\) 的字符，例如 #。字符串 qwq 就变成了 #q#w#q#，中心字符为 w；hooh 变成了 #h#o#o#h#，中心字符为 #。
• 再在 \(S\) 的首尾再加上两个奇怪字符防止越界，例如把 #a#b#b#a# 的首尾加上 $ 和 & 变成$#a#b#b#a#&。

经过变换，字符串 \(S\) 的新长度都是奇数，中心字符只有一个，就只用讨论一次了。

接下来，我们定义数组 \(P\)，\(P[i]\) 是以字符 \(S[i]\) 为中心字符的最长回文串的半径。例如 \(S=\)$#a#b#b#a#& 对应的 \(P\) 是：

\(i\)	0	1	2	3	4	5	6	7	8	9	10
原 \(S\)			a		b		b		a
新 \(S\)	$	#	a	#	b	#	b	#	a	#	&
\(P\)	1	1	2	1	2	5	2	1	2	1	1

如果已经计算出 \(P\)，其中最大的 \(P[i]-1\) 就是答案。例如最大的 \(P[5]=5\)，它对应 #a#b#b#a#，回文串是 abba。这个最长回文串在原字符串的开头位置是 \(\frac{i-P[i]}{2}\)。

不过问题又来了，如何高效计算呢？

核心思想

Manacher 有一个核心思想：回文的镜像也是回文。

• 设当前已经计算出以 \(S[C]\) 为中心的回文，见图阴影部分。
• 它左边的斜线部分是以 \(S[j]\) 为中心的一个回文，回文长度对应 \(P[j]\)。
• 根据回文的镜像原理，\(j\) 以 \(C\) 为轴的镜像部分 \(i\) 也是一个相同的回文。
• 当后面计算以 \(S[i]\) 为中心的回文时，i这部分镜像不用再次检查，这样就减少了重复检查。

不过，细化算法的设计时，问题并不这么简单。\(P[j]\) 可能比 \(P[C]\) 更大，以 \(j\) 为中心的回文串比以C为中心的回文串更长。\(P[i]\) 不一定与 \(P[j]\) 相等，当 \(j\) 的回文串不能被 \(C\) 的左半阴影中包含时，对应的 \(i\) 也会越过右半阴影，扩展到阴影之外右侧的未检查过的字符，可能会扩展出更长的回文。

算法实现

• 设已经计算出了 \(P[0]\sim P[i-1]\)，下一步继续计算 \(P[i]\)。

• 令 \(R\) 是 \(P[0]\sim P[i-1]\) 这些回文串中最大的右端点，\(C\) 是这个 \(R\) 对应的回文串的中心点。

• \(P[C]\) 是已经求得的一个回文串，它的右端点是 \(R\)，且 \(R\) 是所有已经求得的回文串的右端点最大值。

• \(R = C+P[C]\)。在字符串 \(S\) 上，\(R\) 左边的字符已经检查过，\(R\) 右边的字符还未检查。

• 计算 \(P[i]\)。设 \(j\) 是 \(i\) 关于 \(C\) 的镜像点，\(P[j]\) 已经计算出来了。

• 若 \(i \ge R\)，由于 \(R\) 右边的字符都没有检查过，只能初始化 \(P[i] = 1\)，然后用暴力“中心扩展法”求 \(P[i]\)。

• 若 \(i < R\)：

  1. \(j\) 的回文串（下图中 \(j\) 代表的斜线部分）被 \(C\) 的回文串包含，即 \(j\) 回文串的左端点比 \(C\) 回文串的左端点大。按照镜像原理，镜像 \(i\) 的回文不会越过 \(C\) 的右端点 \(R\)，有 \(P[i] = P[j]\)。根据 \(\frac{i+j}{2}= C\)，得 \(j = 2C-i\)，\(P[i] = P[j] = P[2C-i]\)。然后继续用暴力“中心扩展法”完成 \(P[i]\) 的计算。
     
  2. \(j\) 的回文串（\(j\) 的斜线部分）不被 \(C\) 的回文串包含，即 \(j\) 回文串的左端点比 \(C\) 回文串的左端点小。\(i\) 回文串的右端点比 \(R\) 大，但是由于 \(R\) 右边的字符还没有检查过，只能先让 \(P[i]\) 被限制在 \(R\) 之内，有 \(P[i] = w = R - i = C + P[C] - i\)。然后继续用暴力“中心扩展法”完成 \(P[i]\) 的计算。
     
  • 以上两种情况可以一起处理，\(P[i]\) 取两者的较小值，然后用暴力法完成计算。求 \(P\) 的过程是动态规划的思路，所以 Manacher 算法还是一种动态规划算法。

模板代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1.1e7 + 5;
char a[N], s[N << 1];
int n, p[N << 1];    // p[i]：以 s[i] 为回文的中心半径
void change() {    // 变换：添加分隔符
	n = strlen(a);
	int k = 0;
	s[k++] = '$', s[k++] = '#';
	for (int i = 0; i < n; i++) {
		s[k++] = a[i];
		s[k++] = '#';
	}
	s[k++] = '&';    // 首位不一样，防越界
	n = k;
	return;
}
void manacher() {
	int r = 0, c;
	for (int i = 1; i < n; i++) {
		if (i < r) p[i] = min(p[(c << 1) - i], p[c] + c - i);  // 合并处理两种情况
		else p[i] = 1;
		while (s[i + p[i]] == s[i - p[i]]) ++p[i];    // 中心拓展
		if (p[i] + i > r) {
			r = p[i] + i;    // 更新最大的 r
			c = i;
		}
	}
	return;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> a;
	change();
	manacher();
	int ans = 1;
	for (int i = 0; i < n; i++) ans = max(ans, p[i]);
	cout << ans - 1;
	return 0;
}

例题

例 1：Gene Folding

给定一个仅含字符 A、C、G、T 的字符串，可以进行任意次“折叠”操作：选择一个位置（两字符之间），使得该位置向左和向右的子串对称相同（如回文折叠），然后将这两段相同的部分重叠合并。
问经过若干次这样的折叠后，能得到的最短字符串长度。

实现思路

这道题我们可以先思考一下暴力一点的做法，再思考如何让优化。那怎么暴力呢，可以递归循环 Manacher 算法，每次删除最长回文串，直到 \(maxlen−1=1\) 退出循环，直接交会发现 TLE。

所以我们就要想一下怎样避免递归。这时候我们就可以定义一个 \(l\) 和 \(r\)，先用 Manacher 算出所有的 \(p_i\)，在从左到右遍历一遍 \(res\)，如果 \(res_i=\) #，即此回文串为偶回文串，并且 \(i−p_i\le l\)，即有新的偶回文串可以删除，使 \(l=i\)，因为只删一半。\(r\) 同理，只不过是从右往左遍历，使 \(i+pi≥r\) 即可。

最后的答案便是 \(\large\frac{r−l}{2}\)。

---

参考代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e6 + 5;
string DNA, a;
int p[N << 1];
int pos, maxn;
void manacher() {
	a += "$#";
	for (int i = 0; i < DNA.size(); i++) {
		a += DNA[i];
		a += '#';
	}
	int l = 0, r = a.size() - 1;
	for (int i = 1; i < a.size(); i++) {
		if (maxn > i) p[i] = min(p[pos * 2 - i], maxn - i);
		else p[i] = 1;
		while (a[i + p[i]] == a[i - p[i]]) p[i]++;
		if (maxn < i + p[i]) {
			maxn = i + p[i];
			pos = i;
		}
	}
	for (int i = 1; i < a.size(); i++) {
		if (i - p[i] <= l && a[i] == '#') l = i;
	}
	for (int i = a.size() - 1; i > l; i--) {
		if (i + p[i] >= r && a[i] == '#') r = i;
	}
	cout << (r - l) / 2;
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> DNA;
	manacher();
	return 0;
}

例 2：反异或 01 串

给定目标 01 串 \(T\)，初始为空串。每次操作可以在串的左侧或右侧添加 0 或 1，其中添加 0 不限制次数，添加 1 则计数一次。此外，最多可以使用一次“反异或”操作：将当前串 \(s\) 变成 \(s \oplus rev(s)\)（逐位异或）。
问至少需要添加多少个 1 才能构造出 \(T\)。

实现思路

定义“节省度”为使用操作 \(3\) 比不使用时少用的操作 \(1\) 的数量（只有节省度为正时，操作 \(3\) 才有意义）。

手模几组数据，发现操作 \(3\) 的结果 \(S'=S\oplus rev(S)\) 一定是回文串。 因此，操作 \(3\) 可生成的串必是 \(T\) 中的某个回文子串 \(H\)，且“节省度”最大为 \(H\) 中 \(1\) 的个数的一半（向下取整）。

另外，由于操作 \(3\) 生成的字符串回文中心必为 \(0\)，所以 \(T\) 中回文中心为 \(1\) 的回文子串不可以用操作 \(3\) 生成。

只需找出 \(T\) 中含 \(1\) 最多且中心不为 \(1\) 的回文子串，计算其“节省度”\(Δx\) 与 \(T\) 中 \(1\) 的个数 \(cnt\) 即可算出答案 \(ans=cnt−Δx\)。

找回文串用 Manacher 实现。

---

参考代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
constexpr int N = 2e6 + 5;
char a[N], s[N];
int p[N], top, pre[N];
void change() {
	int n = strlen(a);
	s[top = 0] = '$', s[++top] = '#';
	for (int i = 0; i < n; i++) {
		s[++top] = a[i];
		s[++top] = '#';
	}
	s[++top] = '#', s[++top] = '&';
}
void Manacher() {
	int r = 0, c;
	for (int i = 1; i < top; i++) {
		if (i < r) p[i] = min(p[c * 2 - i], p[c] + c - i);
		else p[i] = 1;
		while (s[i + p[i]] == s[i - p[i]]) ++p[i];
		if (p[i] + i > r) {
			r = p[i] + i;
			c = i;
		}
	}
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> a;
	change();
	Manacher();
	for (int i = 1; i <= top; i++) {
		pre[i] = pre[i - 1];
		if (s[i] == '1') ++pre[i];
	}
	int maxn = 0;
	for (int i = 1; i <= top; i++) {
		if (s[i] != '1') {
			int tmp = pre[i + p[i] - 1] - pre[i - p[i]];
			maxn = max(maxn, tmp / 2);
		}
	}
	cout << pre[top] - maxn;
	return 0;
}

例 3：回响形态

给定长度为 $ n $ 的字符串 $ s $，有 $ q $ 次询问，每次给定整数 $ k $。要求计算所有中心为 $ \frac{k}{2} $ 的子串的 border 数量之和。这里的中心是子串起止下标的平均值（可以是小数）。
输出每个询问的结果。

实现思路

本题要求所有以固定中心 \(\large\frac{k}{2}\) 的子串的 border 总数。由于 border 长度对应原串中对称的回文结构，我们可以将问题转化为对一个特殊构造的字符串进行回文计数。

对每个询问的中心 \(c=\large\frac{k}{2}\)，我们找到满足 \(l+r=k\) 的最长子串范围 \([l,r]\)。接着构造一个新串 \(tmp\)：按照交叉顺序 \(s[l],s[r],s[l+1],s[r-1],\cdots\) 排列字符。这样原串中以 \(c\) 为中心的子串对应 \(tmp\) 的一个前缀，且子串的每个 border 长度都对应 \(tmp\) 的一个奇长回文前缀。

对新串进行 Manacher 算法计算每个奇长回文中心的最大半径。每个奇长回文中心 \(i\) 能贡献到所有长度不小于 \(i\) 的前缀，使用差分技巧统计：在 \(i-p[i]+1\) 处加 \(1\)，在 \(i\) 处减 \(1\)，然后做前缀和得到每个前缀包含的奇长回文数。

最后，我们只累加对应原问题有效子串的那些前缀位置，累加值即为答案。由于询问次数很少，每次独立构造新串并跑一次 Manacher，总复杂度为 \(O(nq)\)。

---

参考代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e6 + 20;
int n, Q, k, top;
string s;
char ch[N];
int p[N], f[N], ans;
void init() {
	ans = top = 0;
	for (int i = 0; i <= n * 2 + 5; i++) {
		p[i] = f[i] = 0;
	}
}
void manacher(string in) {
	ch[top = 0] = '$', ch[++top] = '#';
	for (int i = 0; i < in.size(); i++) {
		ch[++top] = in[i], ch[++top] = '#';
	}
	ch[++top] = '&';
	int r = 0, c;
	for (int i = 1; i < top; i++) {
		if (i < r) p[i] = min(p[c * 2 - i], p[c] + c - i);
		else p[i] = 1;
		while (ch[i + p[i]] == ch[i - p[i]]) ++p[i];
		if (p[i] + i > r) {
			r = p[i] + i;
			c = i;
		}
	}
	for (int i = 1; i <= top / 2; i += 2) ++f[i - p[i] + 1], --f[i];
	for (int i = 1; i <= top / 2; i++) {
		f[i] += f[i - 1];
		if (!(i & 1) && ((i >> 1) & 1)) ans += f[i];
	}
}
signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cin >> n >> Q;
	cin >> s;
	s = ' ' + s;
	int x, y, l, r;
	while (Q--) {
		init();
		string tk;
		cin >> k;
		if (k & 1) y = (k + 1) / 2, x = y - 1;
		else x = k / 2 - 1, y = k / 2 + 1;
		for (l = x, r = y; l >= 1 && r <= n; --l, ++r);
		++l, --r;
		for (int i = l, j = r; i <= r; ++i, --j) tk += s[i], tk += s[j];
		manacher(tk);
		cout << ans << '\n';
	}
	return 0;
}

End

课后作业

洛谷课后作业链接：Manacher 作业

参考文献

• Manacher - OI Wiki
• 一些内部资料