记忆化搜索 讲义

基础知识

记忆化搜索是一种通过记录已经遍历过的状态的信息，从而避免对同一状态重复遍历的搜索实现方式。

因为记忆化搜索确保了每个状态只访问一次，它也是一种常见的动态规划实现方式。

知识梳理

记忆化搜索是一种典型的空间换时间的思想，可以看成带备忘录的爆搜递归。

搜索的低效在于没有能够很好地处理重叠子问题。在搜索过程中，会有很多重复计算，如果我们能记录一些状态的答案，就可以减少重复搜索量。动态规划虽然比较好地处理了重叠子问题，但是在有些拓扑关系比较复杂的题目面前，又显得无奈。记忆化搜索正是在这样的情况下产生的，它采用搜索的形式和动态规划中递推的思想将这两种方法有机地综合在一起，扬长避短，简单实用，在信息学中有着重要的作用。

根据记忆化搜索的思想，它是解决重复计算，而不是重复生成，也就是说，这些搜索必须是在搜索扩展路径的过程中分步计算的题目，也就是“搜索答案与路径相关″的题目，而不能是搜索一个路径之后才能进行计算的题目，必须要分步计算，并且搜索过程中，一个搜索结果必须可以建立在同类型问题的结果上，也就是类似于动态规划解决的那种。

记忆化搜索的典型应用场景是可能经过不同路径转移到相同状态的 dfs 问题。更明确地说，当我们需要在有层次结构的图（不是树，即当前层的不同节点可能转移到下一层的相同节点）中自上而下地进行 DFS 搜索时，我们一般可以通过记忆化搜索的技巧降低时间复杂度。

举个例子，就以最常见的斐波那契数列的来讲，它的定义是：$f(0)=1,f(1)=1,f(n)=f(n-1)+f(n-2)$。如果我们使用递归算法求解第 $n$ 个斐波那契数，则对应的递推过程如下：

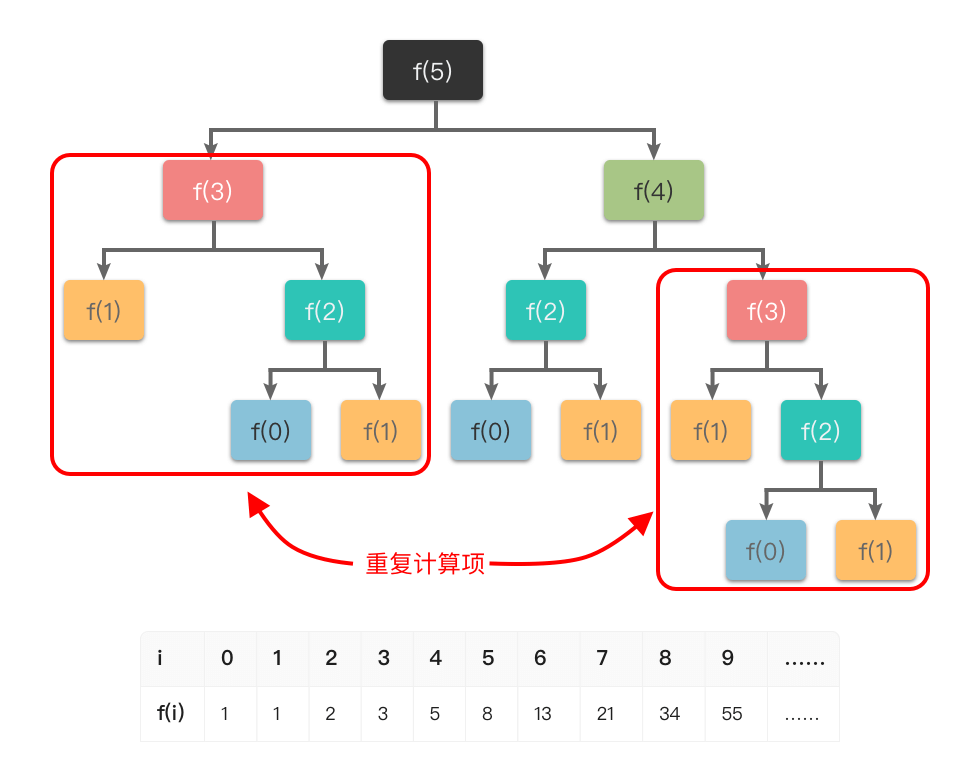
如果使用普通递归算法，想要计算 $f(5)$，需要先计算 $f(3)$ 和 $f(4)$，而在计算 $f(4)$ 时还需要计算 $f(3)$。这样 $f(3)$ 就进行了多次计算，同理 $f(0)$、$f(1)$、$f(2)$ 都进行了多次计算，从而导致了重复计算问题。

为了避免重复计算，在递归的同时，我们可以使用一个缓存（数组或哈希表）来保存已经求解过的 $f(k)$ 的结果。如上图所示，当递归调用用到 $f(k)$ 时，先查看一下之前是否已经计算过结果，如果已经计算过，则直接从缓存中取值返回，而不用再递推下去，这样就避免了重复计算问题。

参考代码

const int N = 3374;
int f[N]; //备忘录，本质是一个哈希表，存的是可变参数和递归返回值之间的映射
int dfs(int t) {
	if (f[t] != 0) return f[t]; //查找一下备忘录，若已进入过该状态，就不再进入了，直接向上返回（相当于剪枝）
	if (t == 0 || t == 1) {
		f[t] = 1;//填备忘录
		return 1;
	}
	return f[t] = dfs(t - 1) + dfs(t - 2);//填备忘录
}

记忆化搜索与递推的区别

记忆化搜索与递推都是动态规划的实现方式，但是两者之间有一些区别。

算法	特点	优点	缺点
记忆化搜索	自顶向下的解决问题，采用自然的递归方式编写过程，在过程中会保存每个子问题的解（通常保存在一个数组或哈希表中）来避免重复计算。	代码清晰易懂，可以有效的处理一些复杂的状态转移方程。有些状态转移方程是非常复杂的，使用记忆化搜索可以将复杂的状态转移方程拆分成多个子问题，通过递归调用来解决。	可能会因为递归深度过大而导致栈溢出问题。
递推	自底向上的解决问题，采用循环的方式编写过程，在过程中通过保存每个子问题的解（通常保存在一个数组或哈希表中）来避免重复计算。	避免了深度过大问题，不存在栈溢出问题。计算顺序比较明确，易于实现。	无法处理一些复杂的状态转移方程。有些状态转移方程非常复杂，如果使用递推方法来计算，就会导致代码实现变得非常困难。

根据记忆化搜索和递推的优缺点，我们可以在不同场景下使用这两种方法。

适合使用「记忆化搜索」的场景：

• 问题的状态转移方程比较复杂，递推关系不是很明确。
• 问题适合转换为递归形式，并且递归深度不会太深。

适合使用「递推」的场景：

• 问题的状态转移方程比较简单，递归关系比较明确。
• 问题不太适合转换为递归形式，或者递归深度过大容易导致栈溢出。

一般解题步骤

基本步骤

我们在使用记忆化搜索解决问题的时候，基本步骤如下：

1. 写出问题的动态规划「状态」和「状态转移方程」。

2. 定义一个“备忘录”（数组或哈希表），用于保存子问题的解。

3. 定义一个递归函数，用于解决问题。在递归函数中，首先检查缓存中是否已经存在需要计算的结果，如果存在则直接返回结果，否则进行计算，并将结果存储到缓存中，再返回结果。

4. 在主函数中，调用递归函数并返回结果。

如何写记忆化搜索

方法一

1. 把这道题的 dp 状态和方程写出来
2. 根据它们写出 dfs 函数
3. 添加记忆化数组

方法二

1. 写出这道题的暴搜程序（最好是 dfs）
2. 将这个 dfs 改成「无需外部变量」的 dfs
3. 添加记忆化数组

例题

从简单到难的几道例题

例 1：[NOIP2005] 采药

山洞里有 $M$ 株不同的草药，采每一株都需要一些时间 $t_i$，每一株也有它自身的价值 $v_i$。给你一段时间 $T$，在这段时间里，你可以采到一些草药。让采到的草药的总价值最大。

$1\le T\le 10^3,1\le t_i,v_i,M\le 100$

朴素的 DFS 做法

很容易实现这样一个朴素的搜索做法：在搜索时记录下当前准备选第几个物品、剩余的时间是多少、已经获得的价值是多少这三个参数，然后枚举当前物品是否被选，转移到相应的状态。

int n, t;
int tcost[103], mget[103];
int ans = 0;

void dfs(int pos, int tleft, int tans) {
	if (tleft < 0) return;
	if (pos == n + 1) {
 		ans = max(ans, tans);
		return;
	}
	dfs(pos + 1, tleft, tans);
	dfs(pos + 1, tleft - tcost[pos], tans + mget[pos]);
}

int main() {
	cin >> t >> n;
	for (int i = 1; i <= n; i++) cin >> tcost[i] >> mget[i];
	dfs(1, t, 0);
	cout << ans << endl;
	return 0;
}

正确实现

如果我们每查询完一个状态后将该状态的信息存储下来，再次需要访问这个状态就可以直接使用之前计算得到的信息，从而避免重复计算。这充分利用了动态规划中很多问题具有大量重叠子问题的特点，属于用空间换时间的「记忆化」思想。

具体到本题上，我们在朴素的 DFS 的基础上，增加一个数组 mem 来记录每个 dfs(pos,tleft) 的返回值。刚开始把 mem 中每个值都设成 -1（代表没求解过）。每次需要访问一个状态时，如果相应状态的值在 mem 中为 -1，则递归访问该状态。否则我们直接使用 mem 中已经存储过的值即可。

通过这样的处理，我们确保了每个状态只会被访问一次，因此该算法的的时间复杂度为 𝑂(𝑇𝑀)

#include <bits/stdc++.h>
#define fast_running ios::sync_with_stdio(false), cin.tie(nullptr)
using namespace std;
int h, m;
int t[105], v[105], f[105][1005];
int dfs(int p, int le) {
	// 第 p 个草药，还剩 le 的时间
	if (f[p][le] != -1) return f[p][le]; // 已经访问过的状态，直接返回之前记录的值
	if (p >= m + 1) return  f[p][le] = 0;
	int r1 = 0, r2 = 0;
	r1 = dfs(p + 1, le);
	if (le >= t[p]) r2 = dfs(p + 1, le - t[p]) + v[p];
	// 状态转移（取和不取）
	return f[p][le] = max(r1, r2); // 最后将当前状态的值存下来
}
signed main() {
	fast_running;
	cin >> h >> m;
	memset(f, -1, sizeof(f));
	for (int i = 1; i <= m; i++) cin >> t[i] >> v[i];
	cout << dfs(1, h);
	return 0;
}

例 2：伊甸园日历游戏

有 $t$ 组数据，每次给定一个日期，两个人轮流对这个日期进行操作：天数 $+1$ 或月份 $+1$。先到达 $\mathrm{2006.11.4}$ 者赢。

正确实现

很明显，我们可以用记搜来求出所有的情况：

#include <bits/stdc++.h>
#define fast_running ios::sync_with_stdio(false), cin.tie(nullptr)
using namespace std;
int month[14] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int x, y, z;
int f[2008][14][33];
bool vis[2008][14][33];
bool check(int Y, int M, int D) {
	if (Y < 2006) return true;
	if (Y == 2006 && M < 11) return true;
	if (Y == 2006 && M == 11 && D < 4) return true;
	return false;
}
int dfs(int Y, int M, int D) {
	if ((Y % 4 != 0 || Y % 100 == 0) && M == 2 && D == 29) return 1; // 判闰年
	if (D > month[M]) ++M, D = 1;
	if (M > 12) ++Y, M = 1;
	// 进位
	if (vis[Y][M][D]) return f[Y][M][D];
	vis[Y][M][D] = true;
	if (D <= month[M + 1] && check(Y, M + 1, D)) f[Y][M][D] = ((dfs(Y, M + 1, D)) ^ 1);
	if (check(Y, M, D + 1)) f[Y][M][D] |= ((dfs(Y, M, D + 1) ^ 1));
	return f[Y][M][D];
}
signed main() {
	fast_running;
	int T;
	cin >> T;
	f[2006][11][3] = 1;
	dfs(1900, 1, 1);
	while (T--) {
		cin >> x >> y >> z;
		if (f[x][y][z]) cout << "YES\n";
		else cout << "NO\n";
	}
	return 0;
}

然后这道题就 AC 了。当然，这道题有更易于编程的方法——找规律。有兴趣的同学可以自己下去尝试。

例 3：分割矩阵

将一个矩形划分为 $n$ 个子矩形，每个矩形的权值定义为矩阵中所有数字的和。求这 $n$ 个子矩阵的权值的均方差（标准差）。

正确实现

均方差（标准差）的公式为：$$x=\sqrt{\frac{{\sum }_{i=1}^n(x_i-\bar{x}{)}^2}{n}}$$（$x_i$ 是第 $i$ 个矩阵的总分，$\bar{x}$为 $n$ 个矩阵总分的平均数）

为了方便计算先把求平均方差的公式展开化简，无论怎样分割平均数都不变。

化简

原式：$\frac{x_1^2+x_2^2+\cdots +x_n^2}{n}-{(\frac{sum}{n})}^2$ ，所以我们需要把 $x$ 的平方和算成最小值。

思路

用 $f[a][b][c][d][k]$ 表示以 $(a,c)$ 为左上角，$(b,d)$ 为右下角，把这个矩阵分成 $k$ 份的最小平方和。之后我们枚举切割位置（横着、竖着），再枚举切割后的两块中一块分成的块数（$1\to k-1$），用记忆化搜索来做就可以了。所以说最后的答案就是：$x=\sqrt{\frac{f[a][b][c][d][k-1]}{n}}$ 。二维前缀和 + dfs 搜索，数据量较小所以能过。

#include <bits/stdc++.h>
#define fast_running ios::sync_with_stdio(false), cin.tie(nullptr)
using namespace std;
int n, m, g;
int mp[15][15], sum[15][15];
double f[15][15][15][15][15];
double cnt;
inline int get_sum(int a, int b, int c, int d) {
    return sum[b][d] - sum[a - 1][d] - sum[b][c - 1] + sum[a - 1][c - 1];
}
double dfs(int a, int b, int c, int d, int k) {
    if (f[a][b][c][d][k] >= 0) return f[a][b][c][d][k];
    if (k == 0) {
        double s = get_sum(a, b, c, d) - cnt;
        f[a][b][c][d][k] = s * s;
        return f[a][b][c][d][k];
    }
    double flag = 1e18;
    for (int i = a; i < b; i++) {
        for (int j = 0; j < k; j++) {
            flag = min(flag, dfs(a, i, c, d, j) + dfs(i + 1, b, c, d, k - j - 1));
        }
    }
    for (int i = c; i < d; i++) {
        for (int j = 0; j < k; j++) {
            flag = min(flag, dfs(a, b, c, i, j) + dfs(a, b, i + 1, d, k - j - 1));
        }
    }
    return f[a][b][c][d][k] = flag;
}
signed main() {
    fast_running;
    cin >> n >> m >> g;
    for (int a = 0; a < 15; a++)
        for (int b = 0; b < 15; b++)
            for (int c = 0; c < 15; c++)
                for (int d = 0; d < 15; d++)
                    for (int k = 0; k < 15; k++) f[a][b][c][d][k] = -1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> mp[i][j];
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            sum[i][j] = mp[i][j] + sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];
        }
    }
    cnt = 1.0 * sum[n][m] / g;
    dfs(1, n, 1, m, g - 1);
    cout << fixed << setprecision(2) << sqrt(f[1][n][1][m][g - 1] / g);
    return 0;
}

End

总结

在实际的编程比赛中，记忆化搜索在骗分上是非常实用的一种方法。一些动态规划题，可以 DFS；数学题，可以 DFS；剪枝的题，更能 DFS。所以，尽管记忆化搜索在打正解的情况下几乎用不到，但在骗分上确实是一个好工具。

课后作业

• 洛谷：P12464，P9504，P1839，P2476，P3609，P8658，P13366，P4796，P13261，P13071，P12622
• Other：不同路径，最长递增子序列