通过动画带你复习排序算法

1. 比较型的算法

1.1. 选择排序

1.1.1. 动画

1.1.2. 逻辑

• 从第一个位置遍历到最后一个位置，找到最小的那个元素，与第一个位置交换
• 从第二个位置遍历到最后一个位置，找到最小的那个元素，与第二个位置交换
• 重复上面的过程，直到所有位置都排好序，最前面已经排好序的位置不用再参与遍历

代码过于简单，不宜展示

1.2. 冒泡排序

1.2.1. 动画

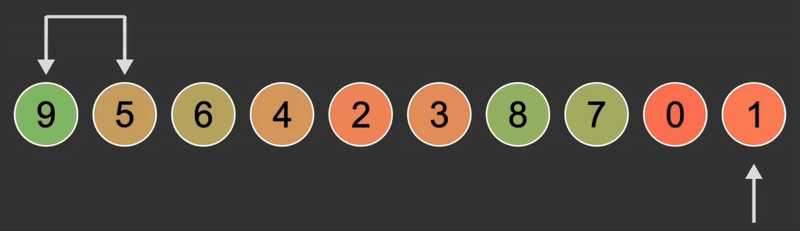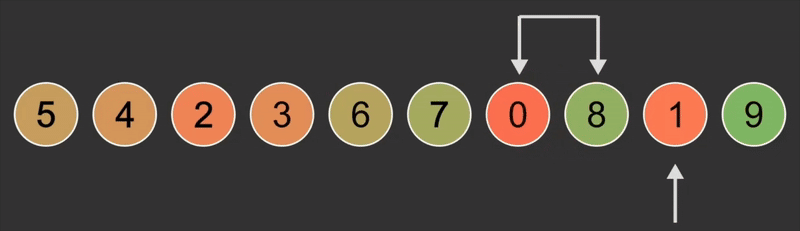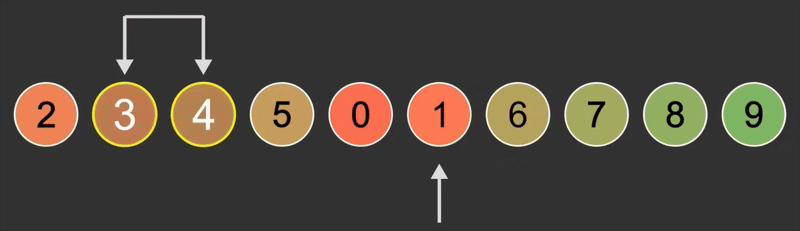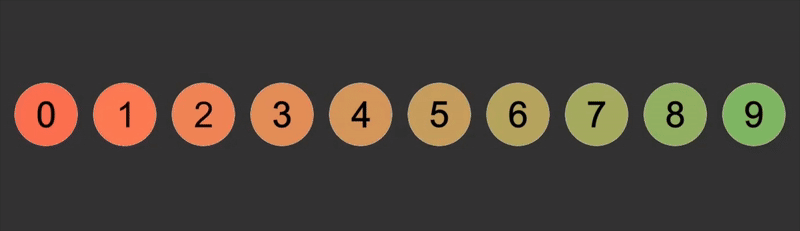
1.2.2. 逻辑

• 将第一个位置与第二个位置比较，如果比后一个位置的元素大，就交换位置，否则不动
• 再将第二个位置与第三个位置比较，如果比后一个位置的元素大，就交换位置，否则不动
• 重复上面的过程一直比到最后一个位置，此时最大的值已经来到了最后
• 重复上面的比较过程，直到所有位置都排好序，最后面已经排好序的位置不用再参与比较

代码过于简单，不宜展示

3. 插入排序

1.3.1. 动画

1.3.2. 逻辑

• 从数组的第二个位置开始，依次与前一个位置比较，如果比前一个位置的元素小，就交换位置，如果比前一个位置的元素大，就停止比较
• 重复这个过程，一直到比完最后一个位置，此时排序结束

代码过于简单，不宜展示

1.4. 归并排序

1.4.1. 动画

1.4.2. 逻辑

• 找到数组的中位，中位左边和右边分别递归处理，每次递归都是找中位拆分成左右两边
• 以左边的递归为例，当递归到只剩下1个元素时，递归就停止，此时不用比较，直接返回
• 递归返回后，此时中位左边和右边分别都排好了顺序（其实递归到最深处返回时，左右两边都只有一个元素），将左右两边的元素合并，当然是按照顺序进行合并。随后，递归再往上返回
• 一直做递归合并的操作，直到递归到最外层，此时所有的元素都排好序了

1.4.3. 代码

class Solution {
    public int[] sortArray(int[] nums) {
        return mergeSort(nums, 0, nums.length - 1);
    }

    /**
     * 归并排序
     */
    public int[] mergeSort(int[] nums, int left, int right) {
        // 左右下标相遇时，说明范围里只有一个元素，无需排序
        if (left == right) {
            return nums;
        }

        // 找到左右下标的中点
        int mid = (left + right) / 2;
        // 排序左边和右边
        mergeSort(nums, left, mid);
        mergeSort(nums, mid + 1, right);
        // 合并左边和右边
        merge(nums, left, right, mid);

        return nums;
    }

    private void merge(int[] nums, int left, int right, int mid) {
        // 存放排序后的元素
        int[] sort = new int[right - left + 1];
        // 左右指针
        int l = left;
        int r = mid + 1;

        // 比较两个指针指向的数，一直到其中一个指针走到终点
        int i = 0;
        while (l <= mid && r <= right) {
            if (nums[l] <= nums[r]) {
                sort[i++] = nums[l++];
            } else {
                sort[i++] = nums[r++];
            }
        }

        // 将另一个指针移动到终点
        while (l <= mid) {
            sort[i++] = nums[l++];
        }
        while (r <= right) {
            sort[i++] = nums[r++];
        }

        // 将 sort 拷贝到 nums 中
        System.arraycopy(sort, 0, nums, left, sort.length);
    }
}

1.5. 快速排序

1.5.1. 动画

1.5.2. 逻辑

• 以最左边的位置为基准数，以最右边的位置为比较数
• 当基准数在左边，且基准数大于比较数时，将基准数与比较数交换位置，相应的，基准位置来到了右边，比较位置向右移动一格
• 当基准数在右边，且基准数小于比较数时，将基准数与比较数交换位置，相应的，基准位置来到了左边，比较位置向左移动一格
• 重复上面的比较过程，一直到基准位置与比较位置相遇。此时，基准数左边都是比它小的数，右边都是比它大的数
• 再分别递归处理基准数左边的元素和右边的元素，直到所有元素都处理结束

这个是双指针法的快排算法，其实还有更优化的方式。另一篇文章详细地分析了双指针快排算法的劣势，以及优化的快排算法。

1.5.3. 代码

class Solution {
    public int[] sortArray(int[] nums) {
        quickSort(nums, 0, nums.length - 1);
        return nums;
    }
    
    /**
     * 快速排序
     * 以左边界为基准，找到基准数应该在的位置，基准数左边的数都比它小，右边的数都比它大
     *
     * @param nums  数组
     * @param left  待排序的左边界
     * @param right 待排序的右边界
     */
    public void quickSort(int[] nums, int left, int right) {
        // 递归终点
        if (left >= right) {
            return;
        }
    
        // 左边为基准数，右边为比较数
        int pivot = left;
        int go = right;
    
        // 只要两个指针未相遇，就一直比较比较
        while (pivot != go) {
            // 基准数在右边
            if (pivot > go) {
                // 如果比较数比基准数大，则交换位置，比较数下标向左移动
                if (nums[pivot] < nums[go]) {
                    // 交换元素位置
                    swap(nums, pivot, go);
                    // 交换指针位置
                    int temp = go;
                    go = --pivot;
                    pivot = temp;
                }
                // 如果比较数不比基准数大，则比较数下标向右移动
                else {
                    go++;
                }
            }
    
            // 基准数在左边
            else if (pivot < go) {
                // 如果比较数比基准数小，则交换位置，比较数下标向右移动
                if (nums[pivot] > nums[go]) {
                    swap(nums, pivot, go);
                    int temp = go;
                    go = ++pivot;
                    pivot = temp;
                }
                // 如果比较数不比基准数小，则比较数下标向左移动
                else {
                    go--;
                }
            }
        }
    
        // 递归处理左右两边
        quickSort(nums, left, pivot - 1);
        quickSort(nums, pivot + 1, right);
    }
    
    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

1.6. 堆排序

1.6.1 动画

1.6.2 逻辑

• 将待排序的数组视为一颗二叉树，i位置节点的左子节点下标就是i * 2 + 1，右子节点下标就是i * 2 + 2
• 将二叉树调整成最大堆，即每一个节点都比左右子节点大。此时顶节点（0位置的元素）就是最大的元素
• 将顶节点与最后一个元素交换位置，并设置一个指针指向最后一个元素，并往前移一位
• 排除掉最后一个元素，剩下的元素构成一个新的二叉树。此时除了顶节点以外，其他位置的元素依然构成最大堆
• 将顶节点下沉到合适的位置，即比较顶节点和左右子节点，如果左右节点较大，将最大的节点与顶节点交换位置，一直重复这个过程直到顶节点下沉到比左右子节点都大
• 再将顶节点与末尾指针指向的那个元素交换，指针向前移一位。并重复上面的过程，直到末尾指针移到第一个位置结束

1.6.3 代码

class Solution {
    public int[] sortArray(int[] nums) {
        heapSort(nums);
        return nums;
    }

    /**
     * 堆排序
     */
    private void heapSort(int[] nums) {
        // 先生成最大堆，将最大的数放到顶节点，即第一个位置
        int heapSize = nums.length;
        for (int i = nums.length - 1; i > -1; i--) {
            heapify(nums, i, heapSize);
        }

        while (heapSize > 1) {
            // 将顶节点与堆最后一个数交换，这样就把最大的数放到了堆的最后面
            swap(nums, 0, --heapSize);

            // 将顶节点下沉，放到合适的位置，重构最大堆
            heapify(nums, 0, heapSize);
        }
    }

    /**
     * 堆排序
     * 以i位置为堆顶节点，构建一个最大堆
     */
    private void heapify(int[] nums, int i, int len) {
        // 算出左子节点
        int index = i * 2 + 1;
        while (index < len) {
            // 算出左右子节点中大的那个
            int large = index + 1 < len && nums[index + 1] > nums[index] ? index + 1 : index;

            // 如果大的子节点比父节点大，就和父节点交换
            if (nums[large] > nums[i]) {
                swap(nums, i, large);

                // 基于子节点向下找
                i = large;
                index = i * 2 + 1;
            } else {
                break;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

2. 非比较型的算法

2.1. 桶排序

2.1.1. 动画

2.1.2. 逻辑

• 准备若干个桶，桶的下标根据数据来决定，一般从0～9。如果是根据员工年龄排序，可以设置100个桶，1～100。（上图桶下标设置成范围了，不如单个值好用）
• 遍历数组，根据数值和桶下标，将对应的元素放到对应的桶里
• 遍历每个桶，将元素依次倒出即可

桶排序对数据样本有要求，数据范围必须是有限的，因为直接关系到桶的数量，桶可以是队列、数组甚至栈。
桶排序是一种思想，下面的计数排序和基数排序是桶排序的两种实现。

2.2. 计数排序

2.2.1. 动画

2.2.2. 逻辑

• 先遍历数组，记下最小值和最大值，这关乎到桶的个数
• 再遍历数组，将元素对应的桶中计数+1
• 如果是对数字进行排序，直接遍历桶，生成一个新数组，即可得到排序后的数组
• 如果是对复杂对象进行排序，则需要使用上图的方式，先计算出桶中计数的前缀和数组
• 从后往前遍历，找到元素对应桶中的计数和，这个元素排序的位置下标就是：计数和-1
• 然后将桶中计数和-1后再放到桶中
• 一直遍历完数组，生成的新数组就是拍好序的

通过计算前缀和，倒序遍历数组计算每个元素的位置的原理解释：

以数组 [ 10 7 4 8 5 ] 为例
计算计数数组：[ 1 1 0 1 1 0 1 ]
                4 5 6 7 8 9 10
计算前缀和数组：[ 1 2 2 3 4 4 5 ]
                  4 5 6 7 8 9 10
前缀和数组每一个元素的含义是：1:小于等于4的元素个数；2（第一个）：小于等于5的元素个数；... 5：小于等于10的元素个数。
以数组中的元素 7 来说，数组中小于等于7的元素一共有3个，那么排序后7一定出现在数组的第3个位置。
为什么把一个元素排好序后，前缀和数组的计数要减1？比如说如果数组中有两个7，第一个7排序后，是第3个位置，那么下一个7排序后一定是第2个位置，所以计数要减1。
上图为什么要从后往前遍历排序？从前往后行不行？从前往后其实也是可以的，从后往前遍历是为了保持原数组中相同顺序元素的原始位置，比如说数组中有2个7，如果从前往后排序，第一个7排序后是第3位，第二个7排序后是第2位，刚好和原数组中顺序相反。而从后往前遍历，则刚好可以保持原来的顺序。这样排序算法的稳定性就比较好。

计算前缀和来排序的思路，在基数排序中也有应用。

2.3. 基数排序

2.3.1. 动画

2.3.2. 逻辑

• 找到原数组中最大的元素，计算出它的位数，比如3位数，需要排序3次
• 准备10个桶，对应的数值分别是0～9
• 先处理个位数字，根据个位数字，将元素放到对应的桶中。随后将桶中元素倒出，如果一个桶中有多个元素，按照先进先出的原则倒出
• 再处理十位数字，根据十位数字，将元素放到对应的桶中。随后将桶中元素倒出，如果一个桶中有多个元素，按照先进先出的原则倒出
• 一直处理完所有的位数，最后倒出的元素就是拍好序的

基数排序是计数排序的升级版，计数排序中桶的个数是按照最小值和最大值来确定的，所以不适用于数值差距较大的场景。
因此基数排序按照元素的位数分别处理，这样每一次排序的数据范围就控制在0～9，只需要10个桶即可。

这里的桶可以是一个队列，刚好满足先进先出的原则。其中这里的桶还可以用数组来实现，其实就是上面的前缀和数组。

如果保证处理十位数字时，个位数字的排序不会被打乱？其实就是靠倒出时的先进先出原则，个位数字排好序后，按照十位数字排序时，个位数小的会先进桶，个位数大的会后进桶，只要按照先进先出的原则，就不会打乱个位数字的顺序。其实换句话说，就是保持排序前数组元素的顺序，计数排序中是靠倒序遍历数组来实现的。

2.3.3. 代码

class Solution {
    public int[] sortArray(int[] nums) {
        return radixSort(nums);
    }

    /**
     * 基数排序
     */
    private int[] radixSort(int[] nums) {
        // 算出数组元素最长的位数
        int maxDigit = getMaxDigit(array);

        // 排序后数组
        int[] orderArray = Arrays.copyOf(array, array.length);
        // 从个位开始遍历，按照每一位数字大小给数字排序
        for (int i = 0; i < maxDigit; i++) {
            // 准备一个长度为10的桶数组
            int[] bucket = new int[10];
            for (int num : orderArray) {
                // 计算对应位数上的数字
                int digitNumber = (int) (num / Math.pow(10, i) % 10);
                // 将相同的数字个数落到对应的桶
                bucket[digitNumber]++;
            }

            // 求桶数组的前缀和，得到每个位置小于等于桶下标的数字个数
            for (int j = 1; j < bucket.length; j++) {
                bucket[j] += bucket[j-1];
            }

            // 从右向左遍历，找到每个元素的位置
            int[] order = new int[orderArray.length];
            for (int j = orderArray.length - 1; j >= 0; j--) {
                // 计算对应位数上的数字
                int digitNumber = (int) (orderArray[j] / Math.pow(10, i) % 10);
                // 取桶里的数字-1得到排序后的下标
                order[--bucket[digitNumber]] = orderArray[j];
            }
            orderArray = Arrays.copyOf(order, order.length);
        }

        return orderArray;
    }

    private int getMaxDigit(int[] nums) {
        int maxDigit = 0;
        for (int num : nums) {
            // 计算最大位数
            int digit = 1;
            int divisor = 10;
            while (num / divisor > 0) {
                digit++;
                divisor *= 10;
            }

            maxDigit = Math.max(maxDigit, digit);
        }
        return maxDigit;
    }
}