关于傅里叶变换Fourier Trans的理解

傅里叶变换玩法无穷无尽，多用做filter使用，此篇仅作入门理解。

• 啥是频域和时域？

时域：以时间为坐标轴的坐标系
频域：以频率为坐标轴的坐标系
很多物理量的定义都是基于单位时间产生的效果或者变化,以时间为参考让我们更容易理解。但容易理解不代表方便使用，或者说方便计算
贯穿时域与频域的方法之一，就是传说中的傅里叶分析。傅里叶分析可分为傅里叶级数（Fourier Serie）和傅里叶变换(Fourier Transformation)。
引入eg：一段音乐按照时域来说，它的音高音低等会随时间一直变化，但如果换个角度，这段音乐却可以看成一段固定的琴谱，从这个角度讲，它其实一直没变！
引入eg：笛卡尔曾说过：人永远无法踏进同一条河流两次，但换个角度，从河流本身来看，河流依然还是那个河流，并没有改变。

• 时域局限性->从声音中分解频率

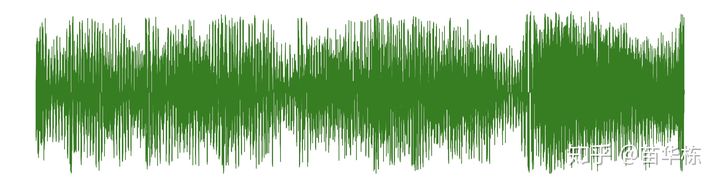
• 低通滤波器

上面的波形图的振幅对应的其实就是声音的强度，如果想让音量大一些，只需要将整体的振幅同比例扩大即可。但如果我想实现低音效果呢（对人声中的低音部分保留或增强，对于人声中的高音部分进行衰减），在时域分析中几乎做不到。但如果在频域中，通过低通滤波器就有可能做到。

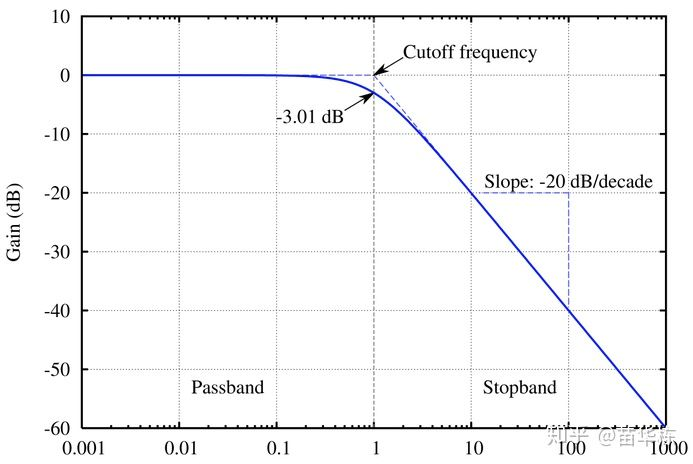
横轴是频率(Hz)，纵轴是声音大小(dB)，图中左侧的横线部分将低音部分保留，图中右侧的斜坡部分，人声中的高音部分进行衰减

• 傅里叶分析使用场景

eg滤波: 把sin（3x）+sin（5x）的曲线给你，但是前提是你不知道这个曲线的方程式，现在需要你把sin（5x）给我从图里拿出去，看看剩下的是什么。这基本是不可能做到的。
但是在频域呢？则简单的很，无非就是几条竖线而已。所以很多在时域看似不可能做到的数学操作，在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松的做到。

eg求解微分方程： 傅里叶变换则可以让微分和积分在频域中变为乘法和除法

• 为什么我们用正弦波？

正弦波是频域中唯一存在的波形
因为正余弦拥有原信号所不具有的性质：正弦曲线保真度。一个正弦曲线信号输入后，输出的仍是正弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的。
且只有正弦曲线才拥有这样的性质，正因如此我们才不用方波或三角波来表示。

• 关于正弦函数

\(y=A*sin(ωx+φ)+k\)，
\(y=A*sin(2∏fx+φ)+k\)，
A——振幅
(ωx+φ)——相位，不同相位决定了波的位置
φ——初相，x=0时的相位；反映在坐标系上则为图像的左右移动
k——偏距，反映在坐标系上则为图像的上移或下移
ω——角频率， 可以控制正弦周期，
周期\(T=2∏/ω\)，
\(ω=2∏f\) ， 角速度ω↗,周期T↘,频率f↗,表现为波形在x轴上收缩，变紧密。
频率\(f=1/T\)
标准正弦函数\(y=sin x\)

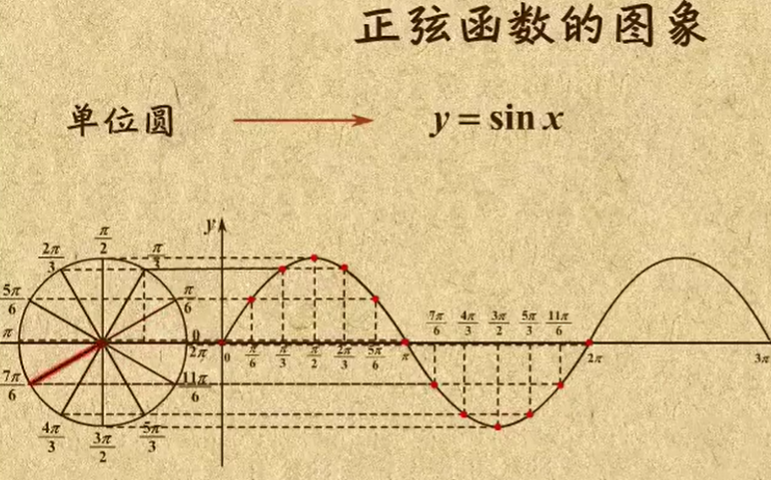
• 傅里叶级数引入-时域到频域转换

*\(y=A*sin(2∏fx+φ) =Asin（φ）+cos(2∏fx）+ Acos（φ）+sin(2∏fx） =\)
无数个正弦函数可以叠加为一个矩形波（随着叠加的递增，所有正弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡，而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。
一个矩形就这么叠加而成了），当然也可以叠加为任意一个波形。

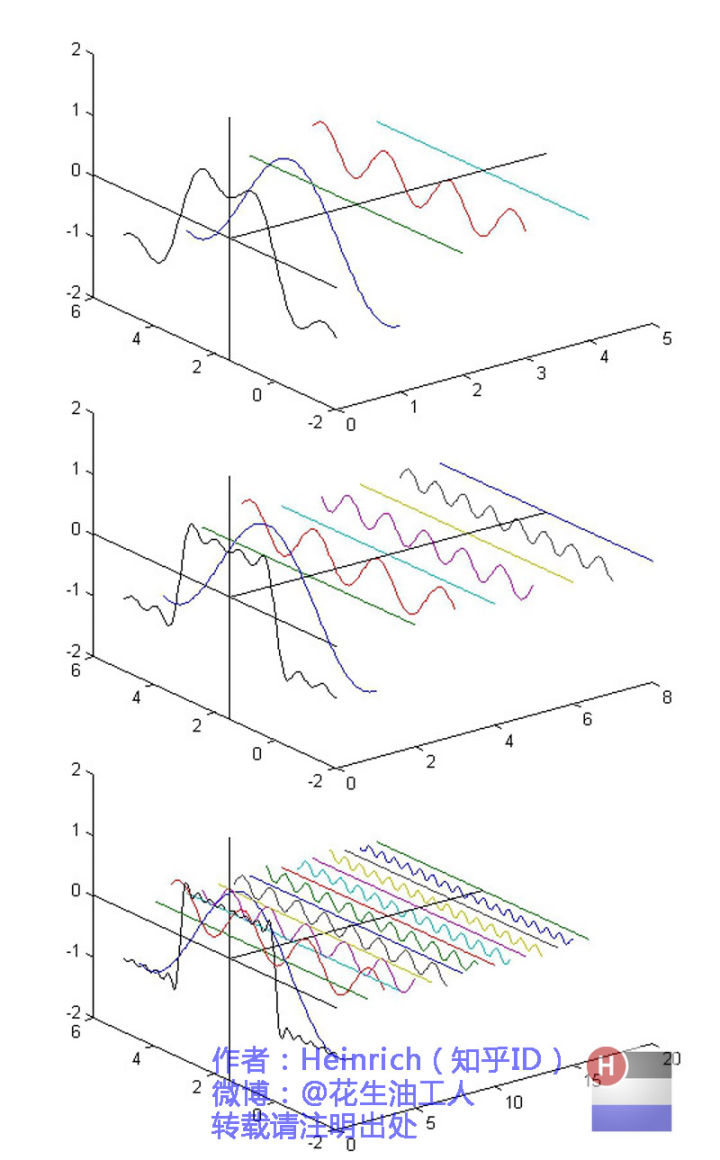
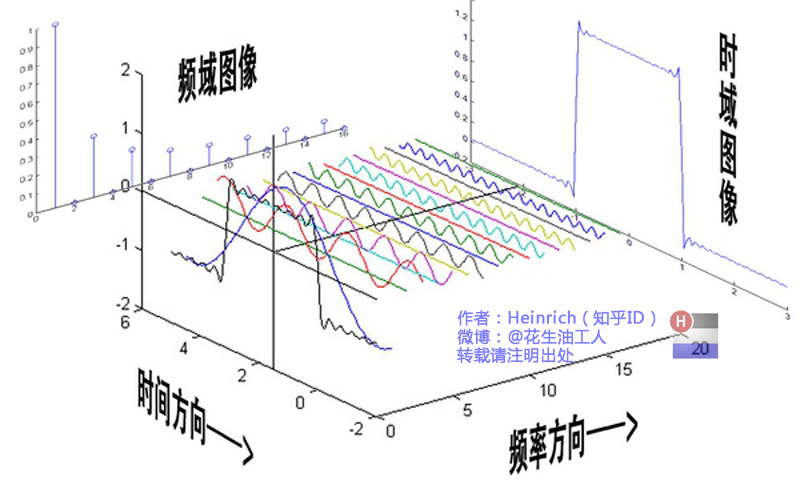
在这几幅图中，最前面黑色的线就是所有正弦波叠加而成的总和，也就是越来越接近矩形波的那个图形。而后面依不同颜色排列而成的正弦波就是组合为矩形波的各个分量。
这些正弦波按照频率从低到高（宽松→紧密）从前向后排列开来，而每一个波的振幅都是不同的。
每两个正弦波之间都还有一条直线，那并不是分割线，而是振幅为0的正弦波！也就是说，为了组成特殊的曲线，有些正弦波成分是不需要的。
这里，不同频率的正弦波我们叫频率分量，在时域中基本单元如果是1s，那么在频域中基本单元我们可以规定为ω，
而当ω==0的时候，T无限大，此时的正弦波相当于一条直线，因此在频率分量中中，0频率也叫做直流分量

• 频域图像（频谱）

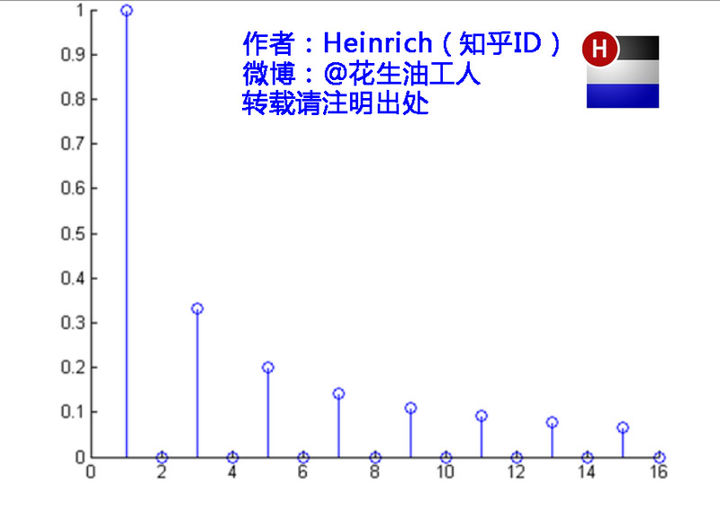
注意：在频谱中我们只能看到每一个对应频率的正弦波的振幅是多少，无法知道相位
可以发现，在频谱中，偶数项的振幅都是0，也就对应了图中的彩色直线。振幅为0的正弦波。

• 傅里叶变换

  将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号。
  傅里叶变换是时域-频域变化分析中最基本的方法之一。

• 什么是傅里叶级数

傅里叶级数（Fourier series）能把类似波的函数表示成正弦波的方式；
它能将任何周期性函数或周期信号分解成一个（可能由无穷个元素组成的）正弦函数和余弦函数的集合
设f(t)是一周期信号,其周期为T。若f(t)在一个周期的能量是有限的，有即

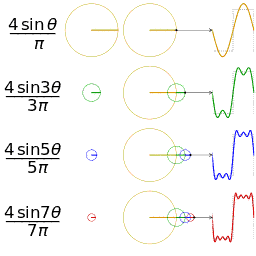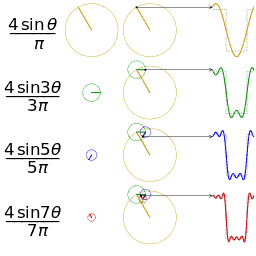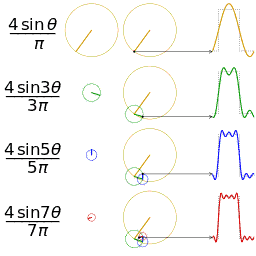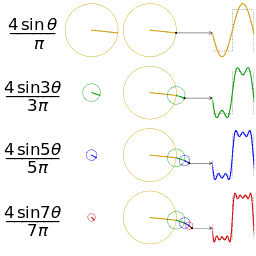
• MATLAB中Fourier transformation的应用

• 什么是FFT?

FFT（FAST傅里叶变换）是一种实现DFT（离散傅里叶变换）的快速算法，是利用复数形式的离散傅里叶变换来计算实数形式的离散傅里叶变换，matlab中的fft()函数是实现该算法的实现。

• 在降噪中的应用?

%——————构造信号————————————————————————————————
Fs =1000;                    %Sample frequency,采样频率， 2 kHz
T = 1/Fs ;                     %Sample period，采样周期,  0.001s
L = 1500;                     %Length of signal
t = (0: L - 1)*T;             % Time vector，行向量（0，0.001，0.002...)

  %构造一个信号，其中包含:
  %幅值为 0.7 的 50 Hz 
  %幅值为 1 的 120 Hz 正弦
S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t);
                                                                    

%————用均值为零、方差为 4 的白噪声扰乱该信号。
X = S + 2*randn(size(t));%返回一个1×1500的矩阵，由随机数组成

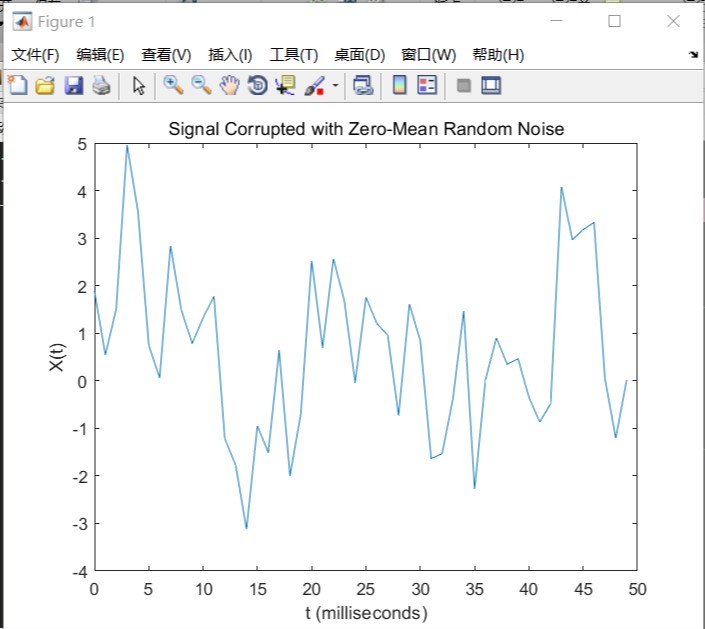
%————时域内绘图——+——————————————————————————————
figure(1);
plot(1000*t(1:50),X(1:50));      %毫秒
title('Signal Corrupted with Zero-Mean Random Noise')
xlabel('t (milliseconds)')
ylabel('X(t)')
%hold on;

 %————对有干扰混合信号进行傅里叶变化————————————————————————————————-——
 Y = fft(X); 
 P2 = abs(Y/L);             %计算双侧频谱P2
 P1 = P2(1 : L/2+1);      %计算单侧频谱P1
 P1 (2: end-1) = 2*P1(2:end -1);
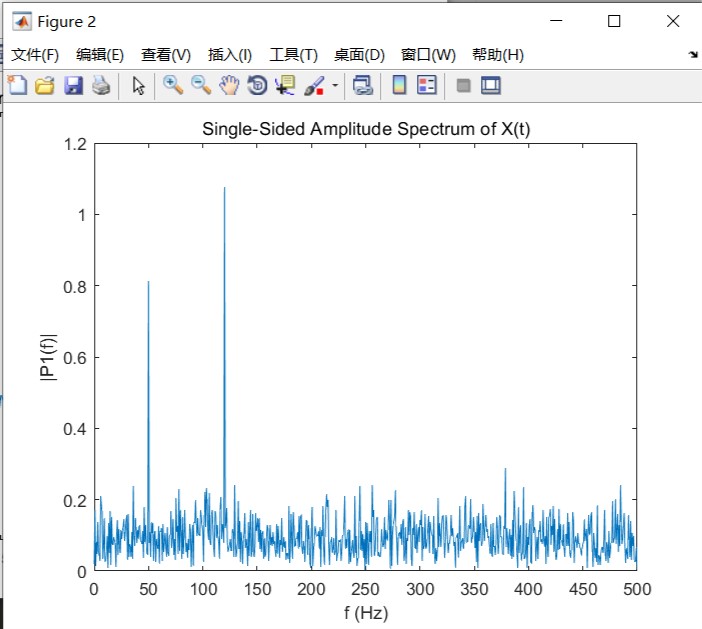
%定义频域f,绘制单侧幅值频谱 P1
%与预期相符，由于增加了噪声，幅值并不精确等于 0.7 和 1。一般情况下，较长的信号会产生更好的频率近似值。
f = Fs * (0 : (L / 2))/L;
figure(2);
plot(f ,P1);
title('Single-Sided Amplitude Spectrum of X(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')


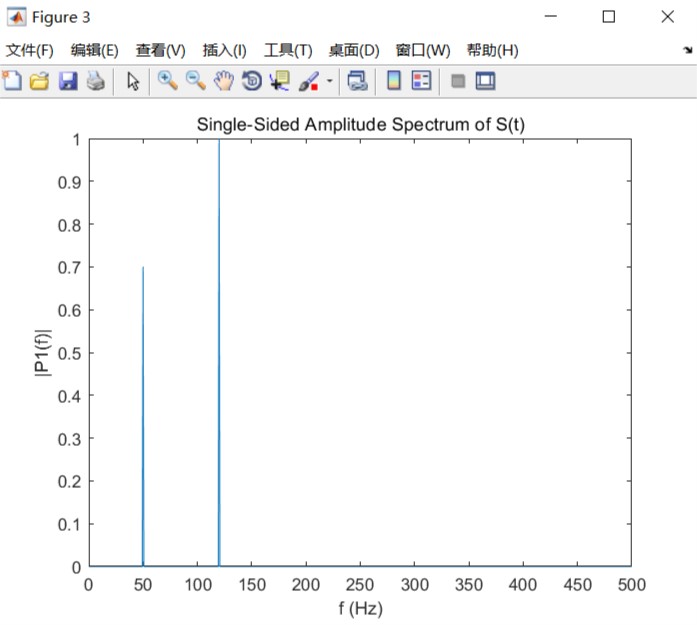
%对原始信号进行傅里叶变换并检索精确幅值 0.7 和 1.0。
Y = fft(S);
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);
figure(3)
plot(f,P1) 
title('Single-Sided Amplitude Spectrum of S(t)')
xlabel('f (Hz)')
ylabel('|P1(f)|')

• 在场景分析中应用

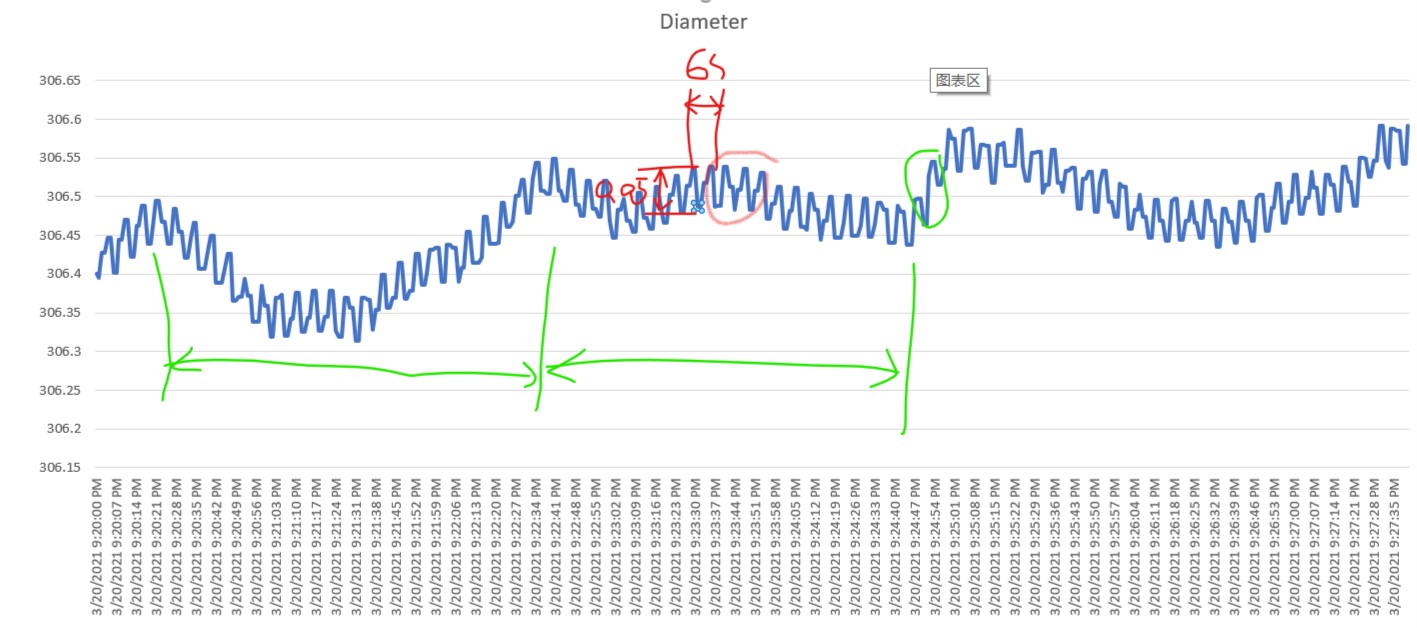
比如我们拿到了一个变量的历史记录，可能有200条，2000条，或者20000条，我们想要探索这个变量变化的周期性规律，如果从时域图分析，我们将很难入手，下面举例：

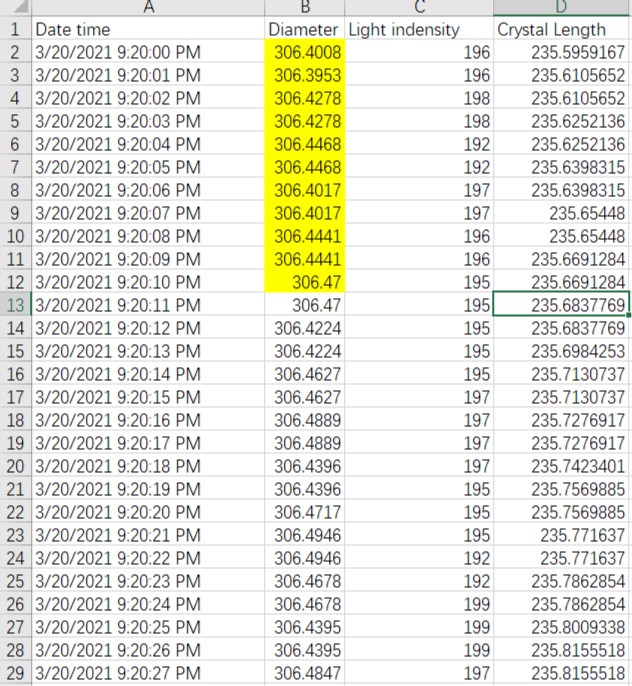
我们想对上图中的直径进行分析，以下是本人所写代码：

clc;
%clear all;
set(0,'defaultfigurecolor','w');
%————读取csv文件数据，取样2000个数据————————————————————————————————
file_path='E:\FFT\RM_1HN_BODY.csv';
Dia_Data = csvread(file_path,1,1,[1,1,2000,1]);
Intensity_Data = csvread(file_path,1,2,[1,2,10,2]);
Length_Data = csvread(file_path,1,3,[1,3,10,3]);
X = Dia_Data';

% M = Dia_Data(:,1);
% M(isinf(M)) = 0;            %确定数组元素是否包含无限值，如果是无限值，替换为1，其他位置 变为0
% M(isnan(M)) = 0 ;           %确定数组元素是否包含NaN，如果有，替换为1，其他位置 变为0
% M = M';

%——————构造信号————————————————————————————————
Fs = 1;                    %Sample frequency, 1 Hz
T = 1/Fs ;                     %Sample period， 1s
L = 2000;                     %Length of signal
t = (0: L - 1)*T;             % Time vector，行向量（0，1，2...)
%————在时域内绘图——+——————————————————————————————
figure(1)
plot( t(1:  2000), X(1:2000) );      %秒
title('Diameter Signal ')
xlabel('t (second)')
ylabel('Dia(mm)')
%hold on;
%————在频域内绘图——+——————————————————————————————

Y = fft(X);
P2 = abs (Y/L);
P1 = P2(1:L/2+1);
P1(1) =0;
P1(2:end-1) = 2*P1(2:end-1);
f = Fs * (0 : (L / 2))/L;
%f=(1:L-1)*Fs/L;
figure(2)
plot(f,P1) 
%plot( f(1:L/2), Y1(1: L/2));
title('Diameter Signal ')
xlabel('频率(Hz)' , 'fontsize',11);
ylabel('幅值(mm)','fontsize',11)

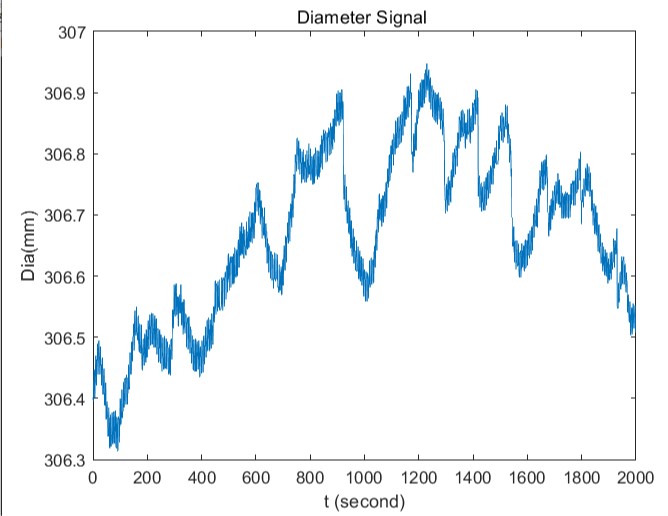
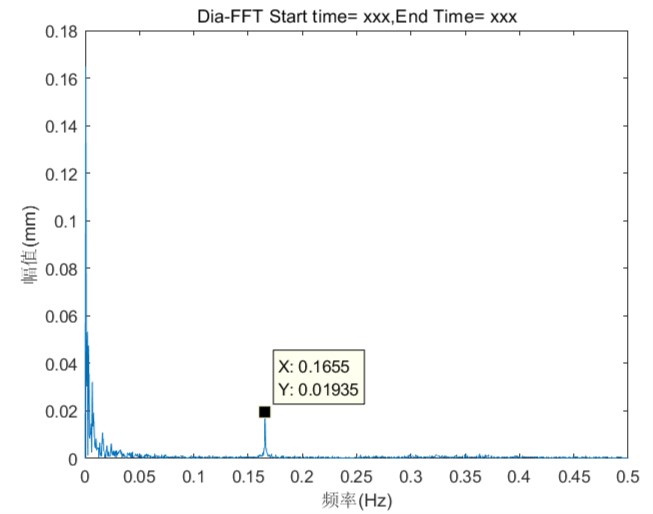
我们发现f=0.1655的频率波对这组数据的影响最大，对应周期为6.04sec，幅值是0.02，是可以对应到时域图中周期相同最多的“有效波形”的